5.4. Методы построения переходных процессов

Для определения числовых значений переходного процесса необ­ходимо иметь его кривую, которую можно получить тремя способа­ми: экспериментально, при помощи моделирования и расчетным путем. Ниже дается обзор некоторых расчетных методов построения переход­ных процессов. Это методы, основанные на решении дифференци­альных уравнений, и частотный метод.

Методы решения диф­ференциального уравнения системы. Эти методы разделяют на точные и приближенные. К точным методам относятся классический и операторный. Различные численные и графические методы решения дифференциаль­ных уравнений являются приближенными.

Классический метод. При решении дифференциального уравнения этим методом возни­кают трудности, связанные с определением корней характеристического уравнения и с решением системы алгебраических уравнений для определения постоянных интегрирования из начальных условий. Эти трудности существенно увеличиваются с возрастанием порядка дифференциального урав­нения. Кроме того, решение дифференциального уравнения значительно услож­няется, когда встречаются не нулевые начальные условия, или правая часть уравнения содержит производные. По этим причинам классический метод в автоматике находит ограниченное применение.

Операторный метод. Решение дифференциального уравнения операторным методом сводится к отысканию оригинала функции по ее известному изображению путем об­ратного преобразования Лапласа. Так, если мы хотим найти переходную функ­цию , то необходимо знать ее изображение и тогда

В свою очередь изображение легко находится при помощи передаточной функции замкнутой системы по известной формуле

Для отыскания оригинала существует несколько способов. Можно использовать таблицы изображе­ний, которыми удобно пользоваться при определении переходных функций ти­повых звеньев, так как в таблицах приведены сравнительно простые выражения для изображений. Однако изображение для автоматических систем обычно является сложной функцией аргумента р. В этом случае для нахождения оригинала лучше подходит теорема разложения.

Операторный метод решения дифференциального уравнения по сравнению с классическим обладает тем преимуществом, что в нем остается только одна трудная операция — определение корней алгебраического уравнения. Вторая трудная операция, связанная с определением по­стоянных интегрирования, отпадает, так как начальные условия учитываются автоматически при составлении передаточной функции системы. Поэтому операторный метод является более удобным, и его часто применяют для решения практических задач автоматического регулирования.

Частотный метод построения переходного процесса. Построение кривой пе­реходного процесса по известным частотным характеристикам системы имеет большое практическое значение, так как не связано с громоздкими вычисления­ми. Кроме того, частотные характеристики можно снять экспериментально.

Этот метод построения переходного процесса основывается на коли­чественной связи между временными и частотными характеристиками, отража­емой преобразованием (интегралом) Фурье

где Х(j) — изображение Фурье функции х (t) и определяется по формуле

.

Согласно этих формул переходная функция (или для единичного входного воздействия) может быть определена так

. (5.42)

Но так как вести расчеты по этой формуле неудобно, из-за наличия комплексных функций под знаком интеграла, то, учитывая известные соотношения

переходный процесс при единичном внешнем воздействии получают по формуле

, (5.43)

либо по формуле

, (5.44)

где Р() и Q() — соответственно вещественная и мнимая частотные характеристики замкнутой системы.

Т

Рис. 5.5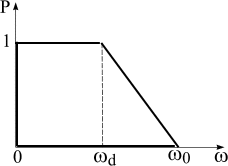

аким образом, по формуле (5.43) или (5.44) при известной Р() или Q() можно рассчитать и построить переходную функцию . Однако в практических задачах функции Р() и Q() оказываются сложными и интегралы в формулах (5.43) и (5.44) трудно вычисля­ются. Поэтому возникла задача построения переходной функ­ции h(t) по формуле (5.43) или (5.44) приближенным методом. Эта задача была решена В.В. Солодовниковым, который предложил приближенный графоаналитиче­ский метод построения кривой переходного процесса. Причем для построения переходной функции обычно используют вещественную характеристику Р().

Суть метода состоит в следующем. График Р() разбивают на типовые трапеции и для каждой трапеции на основании заранее составленных таб­лиц h-функций, рассчитанных при помощи формулы (5.43), строят свой график пере­ходной функции. Искомую переходную функцию находят путем алгебраиче­ского суммирования ординат отдельных составляющих.

Таблицы h-функций составлены для единичной трапеции, которая характеризуется коэффициентом наклона (рис. 5.5). Такая таблица позволяет для заданного значения построить график переходной характеристики h() в функции относительного времени , где текущее время переход­ного процесса. Если высота трапеции не равна единице, то график h() соответ­ственно изменит свой масштаб по оси ординат.

Построение переходной функции h(t) производится в следующей последователь­ности:

1. Одним из известных методов определяют зна­чения и строят график вещественной частотной характеристики Р() замкну­той системы (рис. 5.6,а}.

2. График Р() разбивают на типовые трапеции /, //, ///, для каждой из которых определяют ее параметры , и _0i (рис. 5.5,б).

3. Для каждой из этих трапеций при помощи таблицы h-функций строят график , пересчитывая относительное время в натуральное по формуле .

4. Искомую переходную функцию находят путем алгебраического сумми­рования ординат переходных функций, соответствующих каждой трапеции.

Рис. 5.6

Как показывает практика использования этого метода, его точность вполне достаточна для инженерных расчетов и в значитель­ной степени зависит от точности аппроксимации графика Р(ω) трапециями.