5.3. Пример построения математической модели автоматической системы

Теперь покажем технику математического моделирования автоматической системы на примере функциональной схемой приведенной на рис. 5.3. Эта система выполняет стабилизацию частоты вращения вала, и в качестве объекта управления в ней использован двигатель постоянного тока независимого возбуждения с якорным управлением. В системе установлены два контура обратных связей.

Контур регулирования скорости является главной ОС системы, он охватывает всю систему с выхода на вход и передает информацию в устройство управления о регулируемом параметре . Контур содержит датчик скорости (тахогенератор) и регулятор скорости формирующий закон регулирования по скорости.

Контур регулирования тока - является местной ОС и предназначен для ограничения тока якоря. Контур содержит датчик тока (резистор в цепи якоря) и регулятор тока.

Моделирование системы начинается с разработки математических моделей ее элементов. (Уравнения моделей сопровождаются их операторной формой).

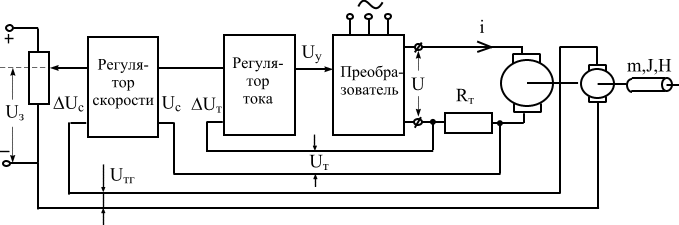
Рис. 5.3. Функциональная схема автоматической стабилизации

частоты вращения вала

Модель регулятора скорости. На вход регулятора скорости поступает сигнал рассогласования по скорости , который преобразуется в этом регуляторе по закону

, (5.31)

. (5.32)

Это так называемый пропорциональный регулятор или П-регулятор.

Модель датчика тока. Датчиком тока служит резистор , включенный последовательно в якорную цепь двигателя. По закону Ома

(5.33)

. (5.34)

Модель регулятора тока. В регуляторе тока сигнал преобразуется в сигнал управления в соответствии с выбранным законом регулирования тока. Используем здесь также П-регулятор, тогда

, (5.35)

. (5.36)

Модель преобразователя. Управление двигателем осуществляется трехфазным преобразователем с линейной зависимостью выходного напряжения u(t) от сигнала управления . Если пренебречь его инерционностью, то можно записать

, (5.37)

. (5.38)

Модель ДПТ. Модель двигателя постоянного тока независимого возбуждения при якорном управлении представлена уравнениями (5.13 и 5.14).

Модель тахогенератора. Обычно тахогенераторы выполняются с линейной статической характеристикой и их инерционностью пренебрегают, поэтому

, (5.39)

. (5.40)

Математическая модель системы. Для составления модели проследим на функциональной схеме путь прохождения воздействий и их преобразования

1)

2) ,

3)

4) ,

5) , .

6)

7)

8)

9)

10)

11) .

Структурная схема соответствующая этим уравнениям представлена на рис. 5.4.

Рис. 5.4.

По этой структурной схеме могут быть построены все динамические характеристики системы. В качестве примера покажем построение одной из них.

Динамика частоты вращения . Так как модель содержит два внешних воздействия и , то в силу ее линейности будем определять передаточные функции по каждому воздействию отдельно.

Реакция системы на изменение задания определяется передаточной функцией относительно точек , при

или после подстановок и упрощений

,

где , , .

Реакция системы на изменение момента нагрузки определяется передаточной функцией относительно точек , при

или

,

где , .

В полученных передаточных функциях знаменатель А(р) является характеристическим уравнением системы и определяется уравнением

,

где ,

,

.

По полученным передаточным функциям легко определяется результирующая характеристика системы

.

Следует заметить, что полученное здесь выражение характеристики представляет собой операторное уравнение, которое требуется с помощью обратного преобразования Лапласа преобразовать в оригинал.