
- •Введение
- •Глава 1 Основные понятия и определения
- •1.1. Начальные сведения о системах автоматического регулирования
- •1.2. Понятие о линейных, нелинейных и линеаризованных моделях
- •1.3. Принципы автоматического управления
- •1.4. Интегральные преобразования Лапласа
- •Глава 2 структурные схемы и их преобразования
- •2.1. Понятие о структурной схеме
- •2.2. Правила преобразования структурных схем
- •2.4. Передаточные функции структурной схемы
- •Глава 3 статические режимы автоматических систем
- •3.1. Понятие о статических характеристиках
- •3.2. Понятие о статическом и астатическом регулировании
- •3.3. Примеры статических и астатических систем
- •3.3.1. Автоматические системы стабилизации напряжения
- •3.3.2. Автоматические системы стабилизации частоты вращения вала
- •Глава 4 динамические звенья
- •4.1. Понятие динамического звена
- •4.2. Динамические характеристики звена
- •4.3. Типовые динамические звенья
- •4.3.1. Безынерционное звено
- •4.3.2. Инерционное (апериодическое) звено первого порядка
- •4.3.3. Инерционное звено второго порядка
- •4.3.4. Интегрирующие звенья
- •4.3.5. Дифференцирующие звенья
- •4.3.6. Запаздывающее звено
- •4.4. Частотные характеристики типовых звеньев
- •Частотные характеристики безынерционного звена
- •Частотные характеристики апериодического звена
- •Частотные характеристики колебательного звена
- •И в показательной форме записывается следующим образом
- •Частотные характеристики дифференцирующего звена
- •Частотные характеристики интегрирующего звена
- •Частотные характеристики запаздывающего звена
- •4.5. Логарифмические частотные характеристики типовых звеньев
- •Глава 5 математическое описание автоматических систем
- •5.1. Общие замечания
- •5.2. Определение начальных условий
- •5.3. Способы записи математических моделей
- •5.2. Примеры математических моделей элементов
- •5.3. Пример построения математической модели автоматической системы
- •Моделирование системы начинается с разработки математических моделей ее элементов. (Уравнения моделей сопровождаются их операторной формой).
- •5.4. Методы построения переходных процессов
- •Глава 6 устойчивость автоматических систем
- •6.1. Понятие устойчивости
- •6.2. Устойчивость линейных систем
- •6.3. Методы определения устойчивости
- •6.4. Критерии устойчивости
- •6.5. Определение областей устойчивости. D – разбиение
- •6.4. Структурная устойчивость автоматических систем
- •6.5. Запас устойчивости
- •6.6. Об устойчивости нелинейных систем
- •Глава 7 качество процессов регулирования
- •7.1. Показатели качества регулирования
- •7.2. Косвенные методы оценки качества регулирования
- •7.3.Точность автоматических систем
- •7.4. Астатизм автоматических систем
- •Глава 8 формирование динамических характеристик
- •8.1. Законы регулирования
- •8.1. Коррекция характеристик ас
- •Глава 9 пример расчета автоматической системы стабилизации
- •9.1 Техническое задание (тз)
- •9.2 Компоновка функциональной схемы
- •9.3. Составление математических моделей сар
- •9.3.1. Статическая модель сар
- •9.3.2. Динамическая модель сар
- •9.3.3. Анализ динамики сар
- •Заключение
- •Библиографический список
4.3.3. Инерционное звено второго порядка
Уравнение динамики звена
![]() ,
(4.20)
,
(4.20)
где
Т –постоянная времени,
![]() коэффициент
демпфирования,
коэффициент
демпфирования,
![]() коэффициент
передачи звена.
коэффициент
передачи звена.
Операторное уравнение и передаточная функция звена следующие:
![]() ,
(4.21)
,
(4.21)
![]() .
(4.22)
.
(4.22)
Отличительной
чертой этого звена является возможность
существования трех видов переходных
характеристик, что определяется корнями
его характеристического уравнения
![]() .
Корни этого уравнения
.
Корни этого уравнения
![]() (4.23)
(4.23)
могут быть вещественными, комплексными или чисто мнимыми, определяя в каждом случае свой переходный процесс. При этом обычно говорят о трех типах звеньев.
Апериодическое
звено второго порядка.
При
![]() корни вещественные, и переходная
функция определяется формулой
корни вещественные, и переходная
функция определяется формулой
![]() .
(4.24)
.
(4.24)
Переходный процесс имеет апериодический характер, протекающий без колебаний (рис. 4.6,а). Можно показать, что в этом режиме звено эквивалентно последовательному соединению двух апериодических звеньев первого порядка с постоянными времени T1, T2 и коэффициентами передачи k1, k2 . Поэтому передаточная функция звена может быть записана также в виде
![]() .
.
Колебательное звено. При 1 корни характеристического уравнения комплексные
![]() ,
,
где
![]() коэффициент
затухания, а
коэффициент
затухания, а
![]() угловая частота свободных колебаний.
Переходная характеристика колебательного
звена определяется уравнением
угловая частота свободных колебаний.
Переходная характеристика колебательного
звена определяется уравнением
![]() ,
,
где
![]() и
и
![]() - соответственно амплитуда, и фаза
свободных колебаний. Переходный процесс
показан на рис. 4.6,б.
- соответственно амплитуда, и фаза
свободных колебаний. Переходный процесс
показан на рис. 4.6,б.
Консервативное
звено. При
![]() корни становятся чисто мнимыми
корни становятся чисто мнимыми
![]() ,
(4.27)
,
(4.27)
и звено представляет собой идеализированный случай звена без потерь. Переходный процесс носит незатухающий колебательный характер (рис.4.6, в).
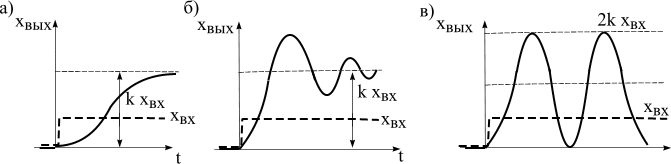
Рис. 4.6. Переходные функции инерционных звеньев второго порядка
Примеры. К инерционным звеньям второго порядка относятся элементы, способные запасать потенциальную и кинетическую энергию и преобразовывать их одну в другую. Такими возможностями обладают: электрические R-L-С контуры; электромеханические устройства, например, двигатели, у которых кинетическая энергия запасается в якоре, а электромагнитная (потенциальная) в якорной цепи; механические элементы, обладающие массой, упругостью и вязким трением и т. д.
Пример 4.2. Для R-L-C контура справедливо уравнение
![]() .
.
Используя
известные формулы:
![]() ,
,
![]() ,
,
![]() ,
получим
,
получим
![]() .
.
Это
уравнение инерционного звена второго
порядка, в котором
![]() ,
,
![]() .
.
4.3.4. Интегрирующие звенья
Интегрирующим
называется звено, в котором производится
интегрирование входного воздействия,
и поэтому в выходном воздействии
обязательно присутствует интеграл
![]() .
.
Идеальное интегрирующее звено. Уравнение динамики звена в дифференциальной и интегральной формах имеют вид
![]() ,
(4.28)
,
(4.28)
![]() .
(4.29)
.
(4.29)
Операторное уравнение и передаточная функция определяются выражениями
![]() ,
(4.30)
,
(4.30)
![]() .
(4.31)
.
(4.31)
Переходную
характеристику легко получить из
уравнения (4.29), если учесть, что при
ступенчатом входном сигнале
![]() и его можно вынести за знак интеграла.
Это дает выражение
и его можно вынести за знак интеграла.
Это дает выражение
![]() .
(4.32)
.
(4.32)
График переходной характеристики приведен на рис. 4.7,а.
Интегрирующее звено с замедлением. Звено описывается дифференциальным уравнением
![]() ,
(4.33)
,
(4.33)
и имеет передаточную функцию
![]() .
(4.34)
.
(4.34)
Отметим, что эту передаточную функцию можно записать еще так
![]() ,
(4.35)
,
(4.35)
что позволяет представить это звено, состоящим из параллельно соединенных звеньев идеального интегрирующего звена и апериодического звена первого порядка. Как показано на рис. 4.7,б, переходная функция звена представляется суммой переходных функций двух звеньев и определяется выражением
![]() .
(4.36)
.
(4.36)
Изодромное звено. Уравнение звена и его передаточная функция
![]() (4.37)
(4.37)
![]() .
(4.38)
.
(4.38)
По виду передаточной функции можно сделать вывод, что изодромное звено составлено из параллельно включенных звеньев - идеального интегрирующего и безынерционного. Переходная функция звена определяется уравнением
![]() (4.39)
(4.39)
и график ее показан на рис. 4.7, в.
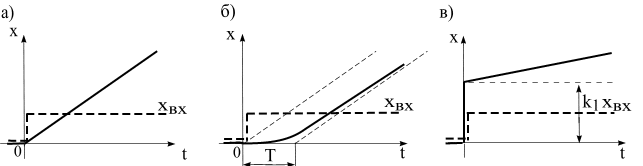
Рис. 4.7. Переходные функции интегрирующих звеньев
Пример 4.3. Идеальным интегрирующим звеном можно считать двигатель постоянного тока в режиме холостого хода. Для цепи якоря справедливо уравнение
![]() .
.
Если
пренебречь потерями напряжений
![]() ,
,
![]() и учесть, что
и учесть, что
![]() ,
где -угол
поворота вала, получим
,
где -угол
поворота вала, получим
![]() .
Интегрирование этого уравнения дает
уравнение идеального интегрирующего
звена, в котором
.
Интегрирование этого уравнения дает
уравнение идеального интегрирующего
звена, в котором
![]() ,
,
![]()
![]() .
.
Пример 4.4. Многие математические операции эффективно выполняются электронными схемами на основе операционных усилителей. Пример такой схемы дан на рис. 4.8,б.
Для этих усилителей характерно три
свойства: 1) усилитель имеет исключительно
большой коэффициент усиления
![]() ;
2) ток, проходящий через усилитель
настолько мал, что при составлении
баланса токов им можно пренебречь; 3)
потенциал в узле “а” можно принять
равным нулю так как
;
2) ток, проходящий через усилитель
настолько мал, что при составлении
баланса токов им можно пренебречь; 3)
потенциал в узле “а” можно принять
равным нулю так как
![]() ,
потому что
,
потому что
![]() .
Покажем, что при данных допущениях,
схема на рис. 4.8,б является идеальным
интегрирующим звеном. Запишем для точки
“а” уравнение баланса токов
.
Покажем, что при данных допущениях,
схема на рис. 4.8,б является идеальным
интегрирующим звеном. Запишем для точки
“а” уравнение баланса токов
![]() ,
,
принимая
![]() и интегрируя это уравнение, получим
и интегрируя это уравнение, получим
![]() .
.
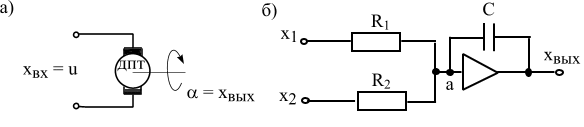
Рис. 4.8. Примеры интегрирующих звеньев
