4.Точки перегиба функции.

Точками перегиба называются такие точки графика функции у = f(x), которые разделяют промежутки выпуклости противоположных направлений этого графика. Рассмотрим функцию у = f(x), график которой представлен на рисунке 5.

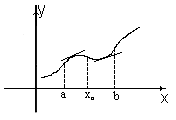Рисунок 5.

Данная функция имеет одну точку перегиба – х₀, которая разделяет два промежутка выпуклости кривой: интервал (a; х₀), где кривая выпукла вверх, и интервал (х₀; b), где кривая выпукла вниз.

Точками перегиба могут служить только критические точки, принадлежащие области определения функции у = f(x), в которых вторая производная f ′′(х) обращается в нуль или терпит разрыв.

Таким образом, для точек перегиба х_о выполняются следующие условия:

1. f′′ (х_о) = 0

2. при переходе через точку перегиба х_о вторая производная меняет знак

Алгоритм нахождения точек перегиба функции с помощью второй производной

1. Найдем область определения функции D(y)

2. Вычислим производную функции f(x)

3. Вычислим вторую производную функции f (x)

4. Решим уравнение f  (x) = 0, найдем точки х₀

5. Исследуем знак второй производной справа и слева от каждой

точки х₀.

6. Запишем ответ.

ПРИМЕР1. Найдите точки экстремума функции f (x) = х ⁴ – 2х³ +2

РЕШЕНИЕ. 1) D(y) = R

2) f  (x) = 4х ³ – 6х²

3) Вычислим вторую производную, находя производную от f  (x):

f  (x) = (f  (x))  = (4х ³ – 6х²)  = 12х² – 12х

4) Решаем уравнение f  (x) = 0: 12х² – 12х = 0, 12х(х – 1) = 0,

12х = 0 или х – 1 = 0, х₁ =0, х₂ = 1

5) Исследуем знак второй производной справа и слева от каждой точки х_0, для чего нанесем на числовую ось найденные точки и вычислим значение второй производной на полученных интервалах:

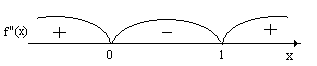Рисунок 6

f  (-1) = 12  (-1) ² – 12  (-1) = 12  1 + 12 = 24 > 0, ставим знак «+»

f  (0,5) = 12  (0,5) ² – 12  0,5 = 12  0,25 - 6 = 3 – 6 = -3 < 0, ставим знак «-»

f  (2) = 12  2 ² – 12  2 = 12  4 - 24 = 48 – 24 = 24 > 0, ставим знак «+»

Знаки меняются (т.е. меняется направление выпуклости), следовательно, найденные точки являются точками перегиба.

5) Ответ: х = 0; x = 1 – точки перегиба.

ПРИМЕР2. Найдите точки экстремума функции f (x) = х ⁴ – 6х ² +5

РЕШЕНИЕ. 1) D(y) = R

2) f  (x) = х ³ – 12х

3) f  (x) = (х ³ – 12х)  = 3х ² – 12

4): 3х ² – 12 = 0, 3 (х ² – 4) =3 (х – 2)(х + 2) = 0,

х + 2 = 0 или х – 2 = 0, х₁ = - 2, х₂ = 2

5)

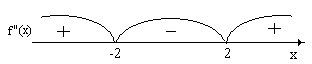Рисунок 6

f  (-3) = 3  (-3) ² – 12 = 3  9 - 12 = 27 – 12 = 15 > 0

f  (0) = 3  (0) ² – 12 = 3  0 - 12 = 0 – 12= -12 < 0

f  (3) = 3  (3) ² – 12 = 3  9 - 12 = 27 – 12 = 15 > 0

5) Ответ: х = -2; x = 2 – точки перегиба.

ЗАДАНИЕ №3

Найдите промежутки монотонности функций:

1. f (x) = х² - 2х + 2

2. f (x) = х² + 3х - 5

3. f (x) = 4х - х ² + 2

4. f (x) = х² - х + 3

5. f (x) = х⁴ - х² + 1

6. f (x) =3х² - х ³ + 2

ЗАДАНИЕ №4

Найдите точки экстремума функций:

1. f (x) = х² - х + 7

2. f (x) = х⁴ - х² + 1

3. f (x) =3х² - х ³ + 2

4. f (x) = х³ - 3х + 1

5. f (x) = х³ - 3х² - 4

6. f (x) = х³ + 3х² - 2

ЗАДАНИЕ №5

Найдите интервалы выпуклости функций:

1. f (x) = 6х² – х⁴ + 3

2. f (x) = х⁴ - 3х² + 1

3. f (x) =3х² - х ³ + 2

4. f (x) = х³ - 3х + 1

5. f (x) = х³ - 3х² - 4

6. f (x) = х³ + 3х² - 2

ЗАДАНИЕ №6

Найдите точки перегиба функций:

1. f (x) =3х² - х + 7

2. f (x) = х⁴ - 6х² + 1

3. f (x) =3х² - х ³ + 2

4. f (x) = х³ - 3х + 1

5. f (x) = х³ - 3х² - 4

6. f (x) = 3х⁴ + 2х³ - 2

Тест Исследование функции с помощью производной.

1.Определите тип критической точки, если в ней значение второй производной

равно -3:

1. max

2. min

3. перегиб

2.Признаком убывания функции на данном интервале является:

1. положительное значение первой производной на данном интервале

2. отрицательное значение первой производной на данном интервале

3. положительное значение второй производной на данном интервале

4. отрицательное значение второй производной на данном интервале

3.Критическими точками функции называются такие точки, в которых:

1. значение функции равно нулю

2. значение аргумента равно нулю

3. значение первой производной функции равно нулю

4. значение второй производной функции равно нулю

4.Признаком выпуклости интервала кривой вверх является:

1. положительное значение первой производной на данном интервале

2. отрицательное значение первой производной на данном интервале

3. положительное значение второй производной на данном интервале

4. отрицательное значение второй производной на данном интервале

5.Областью определения функции является:

1. Множество всех ее значений

2. Множество всех значений аргумента функции

3. Множество всех значений производной

4. Множество всех ее корней

6.Областью значения функции является:

1. Множество всех ее значений

2. Множество всех значений аргумента функции

3. Множество всех значений производной

4. Множество всех ее корней

7.Признаком минимума функции является:

1. равенство нулю в данной точке первой и второй производной функции

2. равенство нулю в данной точке первой производной функции и положительное значение второй производной

3. равенство нулю в данной точке первой производной функции и отрицательное значение второй производной

8.Определите тип критической точки, если в ней значение второй производной

равно 7:

1. max

2. min

3. перегиб

9.Признаком возрастания функции на данном интервале является:

1. положительное значение первой производной на данном интервале

2. отрицательное значение первой производной на данном интервале

3. положительное значение второй производной на данном интервале

4. отрицательное значение второй производной на данном интервале

10.Признаком максимума функции является:

1. равенство нулю в данной точке первой и второй производной функции

2. равенство нулю в данной точке первой производной функции и положительное значение второй производной

3. равенство нулю в данной точке первой производной функции и отрицательное значение второй производной

11.Определите тип критической точки, если в ней значение второй производной равно 0:

1. max

2. min

3. перегиб

12.Признаком выпуклости интервала кривой вниз является:

1. положительное значение первой производной на данном интервале

2. отрицательное значение первой производной на данном интервале

3. положительное значение второй производной на данном интервале

4. отрицательное значение второй производной на данном интервале

13.Необходимым условием точки перегиба функции является:

1. равенство нулю в данной точке второй производной функции

2. равенство нулю в данной точке первой производной функции и положительное значение второй производной

3. равенство нулю в данной точке первой производной функции и отрицательное значение второй производной