Раздел II. Исследование функции с помощью производной

Целью исследования функции с помощью производной является нахождение характерных особенностей функции и, на основе этих данных, построение графика функции.

К характерным особенностям функции можно отнести критические точки функции (экстремумы и перегибы); промежутки монотонности; интервалы выпуклости.

Вспомним основные правила и понятия:

1. ПРОМЕЖУТКИ МОНОТОННОСТИ – это промежутки возрастания и убывания функции.

Рассмотрим функцию у = f(x), график которой представлен на рисунке 1

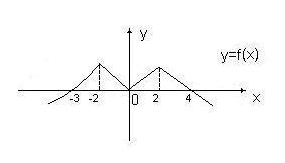Рисунок 1.

Данная функция имеет несколько промежутков монотонности. Так на интервалах

(-; -2) и (2; ) функция возрастает, а на интервалах (-2; 0) и (2; 4) функция убывает. Для нахождения промежутков монотонности с помощью производной используют следующие признаки:

Признак возрастания функции.

Если на некотором промежутке f′ (х) > 0, то функция на этом промежутке возрастает.

Признак убывания функции.

Если на некотором промежутке f′ (х) < 0, то на этом промежутке функция убывает.

При решении задач на нахождения промежутков монотонности необходимо придерживаться следующего алгоритма:

Алгоритм нахождения промежутков монотонности функции с помощью первой производной

1. Найдем область определения функции D(y)

2. Вычислим производную функции f(x)

3. Решим неравенство f(x)  0 (или f(x)  0)

4. Пользуясь признаками, определим интервалы возрастания и убывания функции.

5. Запишем ответ.

ПРИМЕР 1. Найдите промежутки возрастания и убывания функции у = 2х² - 6х + 1. 1) Для нахождения области определения функции необходимо найти множество всех значений аргумента, при которых функция имеет смысл. В данном случае, функция имеет смысл (т.е. может быть определена) для всех действительных чисел (множество R). Таким образом, D(y) = R.

2)находим производную у = 4х – 6

3) задаем неравенство 4х – 6  0, 4х  6, х  1,5

4) на интервале (1,5; ) производная положительна, следовательно, функция возрастает, и наоборот, на интервале (- ; 1,5) производная отрицательна, следовательно, функция убывает.

5 ) записываем ответ: f (х) возрастает при х (1,5; ); f (х) убывает при х  (- ; 1,5)

ПРИМЕР 2. Найдите промежутки возрастания и убывания функции у = 5 - х² + 7х

РЕШЕНИЕ. 1) D(y) = R.

2) у =-2х + 7

3) -2х + 7  0, -2х  -7, х  3,5

4) при х  3,5 , у  0  функция возрастает

при х  3,5 , у  0  функция убывает

5) Ответ: f (х) возрастает при х (3,5; ); f (х) убывает при х  (-; 3,5)

2.Точки эксремума.

Рассмотрим функцию у = f(x), график которой представлен на рисунке 2.

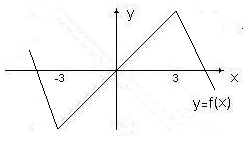Рисунок 2.

Данная функция имеет две точки экстремума – точку минимума (х = - 3) и точку максимума (х = 3). Существует несколько способов нахождения точек экстремума. Мы будем находить точки экстремума с помощью второй производной:

Второе правило определения экстремумов функции:

а) если в данной критической точке х_о вторая производная функции f ′′ (х_о) > 0,

то х_о - минимум функции;

b) если в данной критической точке х_о вторая производная функции f ′′ (х_о) < 0,

то х_о - максимум функции.

(Вспомним, что критическими точками функции называются точки, в которых производная функции равна нулю или не определена).