ЧОУ СПО «Казанский кооперативный техникум»

Методические рекомендации по решению задач на тему

«Производная функции»

Шулаева И.В.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Данное методическое пособие предназначено для студентов очного и заочного отделений образовательных учреждений среднего профессионального образования, изучающих математику.

Пособие разработано с целью научить студентов первого и второго курсов вычислять производные различных функций, используя правила дифференцирования и таблицы производных. А также проводить исследование функции с использованием методов математического анализа.

Пособие состоит из двух разделов: «Вычисление производной функции» и «Исследование функции с помощью производных». Каждый раздел содержит основные понятия, правила и формулы по изучаемой теме, алгоритмы решения задач по исследованию функции. Приводится подробное решение различных примеров и задач. В конце каждого раздела помещены задания для самостоятельной работы и тестовые вопросы для контроля остаточных знаний. Тестирование может быть проведено как письменно, так и с помощью компьютера.

Раздел 1. Понятие производной

  При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f(x) и обозначают символом

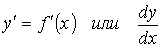
  Тот процесс, с помощью которого из данной функции f(x) получают новую функцию f ' (x), называют дифференцированием и состоит он из следующих трех шагов:   1) даем аргументу x приращение D x и определяем соответствующее приращение функции D y = f( x+D x) - f(x);   2) составляем отношение

;

  3) считая x постоянным, а D x стремящимся к нулю, находим

,

который обозначаем через f ' (x), как бы подчеркивая тем самым, что полученная функция зависит лишь от того значения x, при котором мы переходим к пределу.   

О п р е д е ле н и е: Производной y ' =f ' (x) данной функции y=f(x) при данном x называется предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю, если, конечно, этот предел существует, т.е. конечен.   Таким образом,

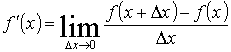, или .

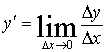  Заметим, что если при некотором значении x, например при x=a, отношение

при стремлении D x к нулю не стремится к конечному пределу, то в этом случае говорят, что функция f(x) при x=a (или в точке x=a) не имеет производной или не дифференцируема в точке x=a.

Вычисление производной функции

При решении задач на вычисление производных различных функций необходимо использовать правила дифференцирования и таблицу производных. Вспомним основные правила дифференцирования:

1. Производная постоянной. Пусть у = С, где С – постоянное число.

Тогда С = 0 , производная постоянной равна 0. (1)

2. Производная функции у = х. В этом случае производная равна 1.

х = 1 (2)

3. Производная алгебраической функции. Пусть функция у представлена в виде суммы нескольких функций: у = u + v – w, где u, v, w – функции от аргумента х, имеющие производные по х. Тогда производная вычисляется по формуле:

(u + v – w)  = u + v – w. (3)

Производная алгебраической суммы конечного числа функций равна сумме производных слагаемых.

Например: у = х + 3, тогда у = (х)  + (3)  = 1 + 0 = 1

4. Производная произведения двух функций. Пусть у = uv, где где u, v – функции от аргумента х, имеющие производные по х. Тогда производная вычисляется по формуле: (uv)  = u v + v u (4)

Производная произведения двух функций равна сумме произведений производной первой функции на вторую и первой функции на производную второй..

5. Производная произведения постоянной на функцию. Пусть у = Сu, где С – постоянное число, а u - функция от аргумента х, имеющая производную по х.

Тогда (Cu)  = Cu (5)

и (Cx)  = C (6)

Производная произведения постоянной на функцию равна произведению постоянной на производную функции (постоянную можно вынести за знак производной).

Например: 1) у = 5 (4 + х), тогда у = 5 (4 + х) = 5 ((4) +(х) ) = 5 (0 + 1) = 51= 5

2) у = 12х, у = 12 (х)  = 121 = 12

Кроме того, при вычислении производных используют таблицу производных:

функция	производная
х n	n ∙х n-1
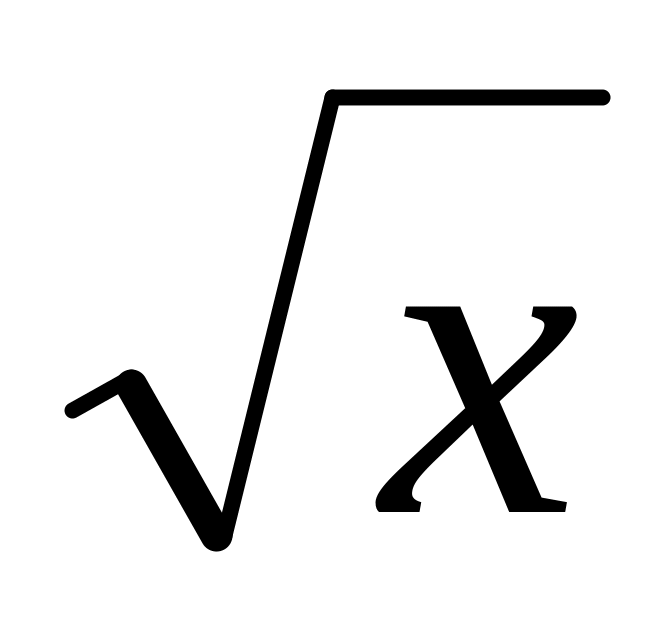
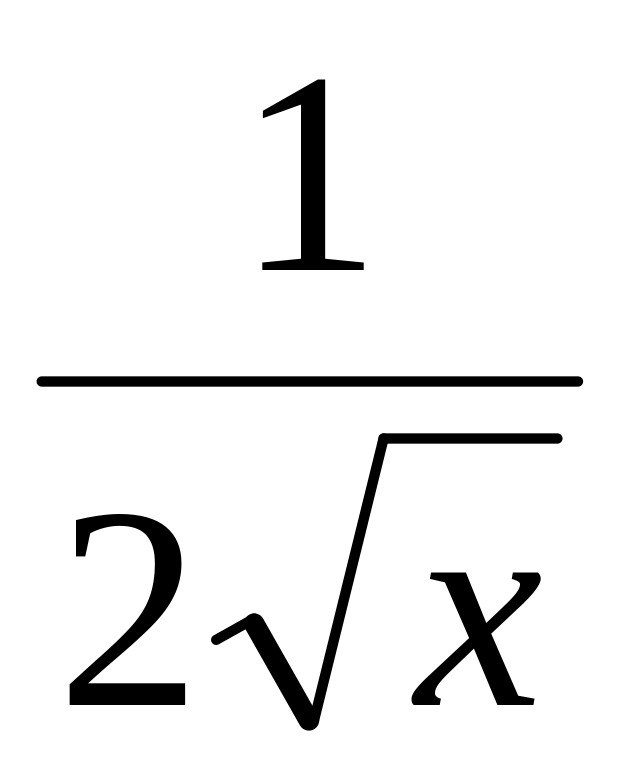
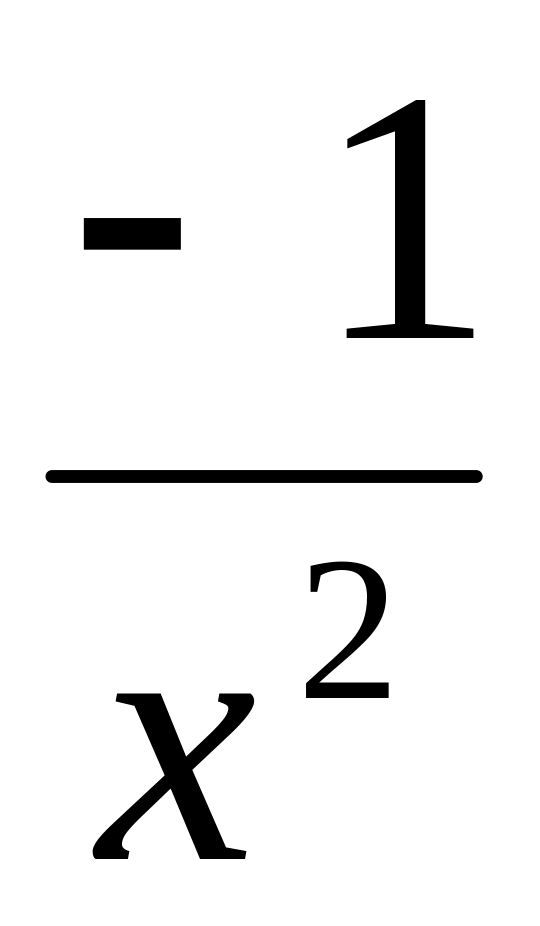
sin х	cos х
cos х	- sin х
tg х
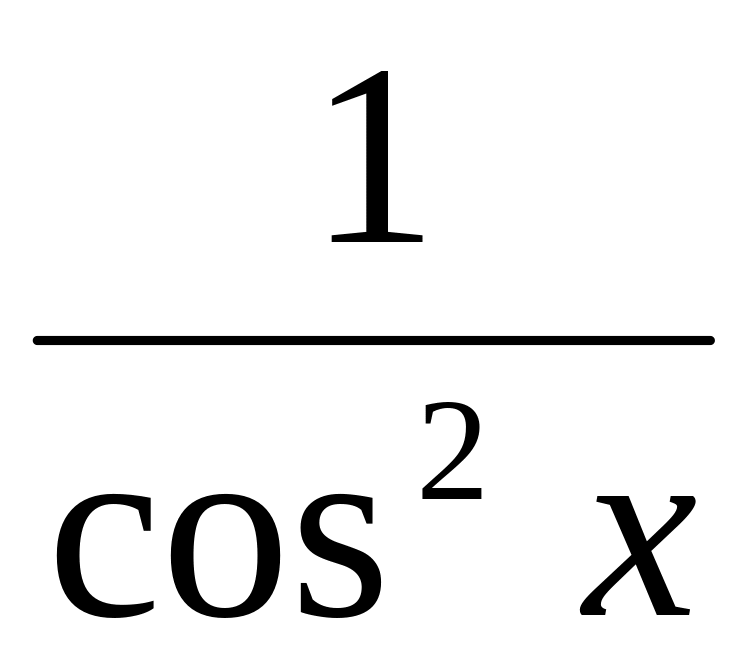
ctg х
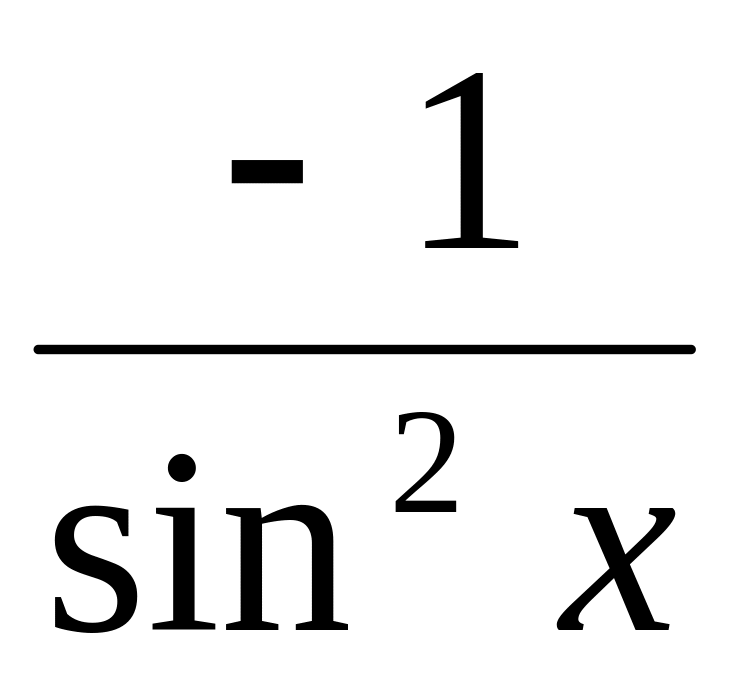
℮ х	℮ х
а х	а х ∙ ln а
ln х
log a х
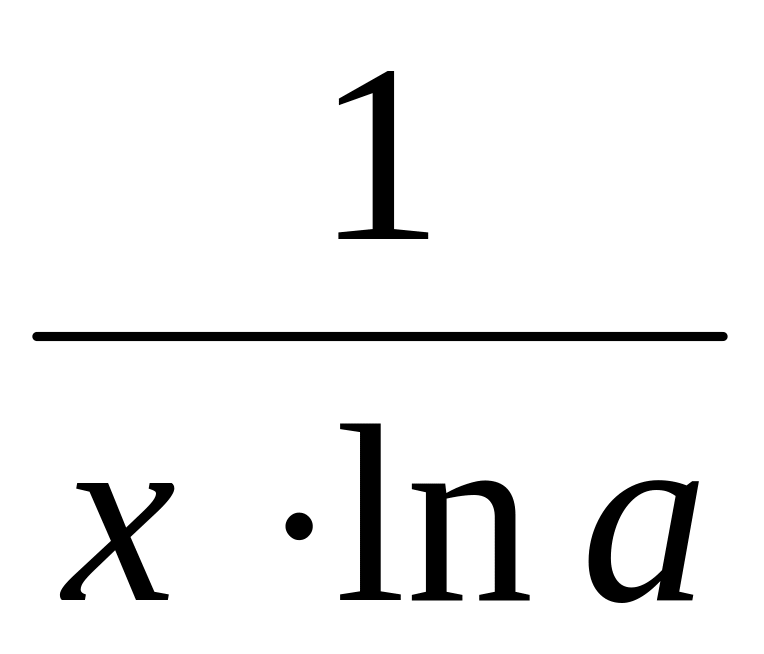
arcsin х
arccos х	-
arctg х
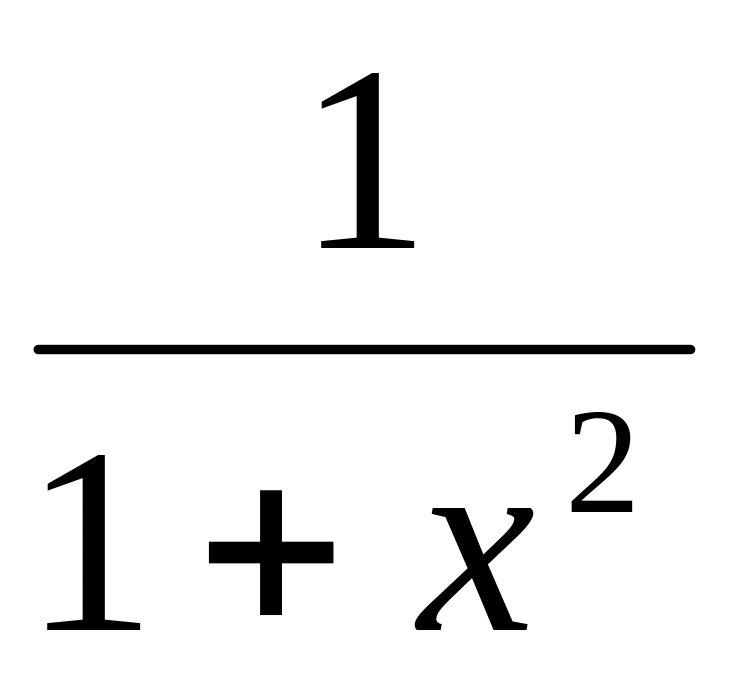
arcсtg х	-

Рассмотрим примеры на вычисление производных:

Пример 1. у = 4x⁴ + sin x + log ₃ x -2 ^х + 8.

Для вычисления производной данной функции необходимо воспользоваться формулой (3): (u + v – w)  = u + v – w

т.е. мы будем находить производную от каждого слагаемого:

у = 4(x⁴)  + (sin x)  + (log ₃ x )  - (2 ^х)  + (8) 

Значение производных данных функций находим в таблице:

(x⁴)  = 4х^4-1 = 4х³ (по формуле (х ⁿ)  = n х ^n-1); (sin x)  = cos x;

(log ₃ x )  = (по формуле (log _а х)  = , где а = 3);

(2 ^х)  = 2 ^х  ln 2 (по формуле (а ^х)  = а ^х  ln а, где а = 2).

Таким образом, у = 4  4х³ + cos x + - 2 ^х  ln 2 + 0

окончательно: у = 16х³ + cos x + - 2 ^х  ln 2

Примеры №2 и 3 решаем аналогично:

Пример 2. у = arctg x + 14x⁵ – ln x + 11

у = (arctg x )  + 14(x⁵)  – (ln x)  + (11) 

у = + 145х⁴ - + 0

у = + 70х⁴ -

Пример 3. у = 3cos x – log ₅x – +

у = 3(cos x) – (log ₅x) – ( ) + ( )

у = 3(-sin x) - - +

у = - 3sin x - - -

Пример 4. у = cos x  (2 + sin x)

Для вычисления производной необходимо воспользоваться формулой (4):

(uv)  = u v + v u

Запишем производную в общем виде:

у = (cos x)   (2+sin x) + cos x  (2 + sin x) 

По таблице находим производную множителей:

у = sin x  (2+sin x) + cos x  (0 + cos x) = 2 sin x + sin² x + cos² x ,

т.к. sin² x + cos² x = 1, то у = 2 sin x + 1.

Пример 5. у = arctgх  (6x³ + 14х)

у = (arctg х)  (6x³ + 14х) + arctg х  (6x³ + 14х)  находим значения производных по таблице: у =  (6x³ + 14х) + arctg х  (6  3х² + 14)

окончательно: у =

Пример 6. y = (5х – 7)  e^x

y = (5х – 7)  e^x + (5х – 7)  (e^x)

y = (5 – 0)  e^x + (5х – 7)  e^x = 5e^x + (5х – 7)  e^x = e^x  (5 + 5x -7)

окончательно: у = e^x  (5x -2)

Для закрепления полученных навыков выполните задание №1:

Найдите производные функций:

1. у = 12х + 3х² - 4 + - 3sin x

2. у = 5x⁴ – 3x³ + 2x -7 +

3. у = 7cos x  (2 + arcsin x)

4. у = 2x⁶ – 3^x + 13x² -27 + tg x

5. у = 6cos x (5x + sin x)

6. у = (11x³ – 5)×cos x

7. у = 7 ^x × (12 + 2x)

8. y = + log₂x – 5x⁷ – 4

9. y = e^x × (3x⁵ – 8)

10. y = ctg x + 6^x – lnx + 2

11. y = log₄x × (3x - )

12. y = 5x³ - 2 + 4cos x – 11