Решение типовых задач

1. Выполнить действия с матрицами:

а)

Сначала умножаем матрицу на число, затем вычитаем из одной матрицы другую.

б) .

Нужно перемножить две матрицы C = AB. Это возможно в случае, если число столбцов матрицы A равно числу строк матрицы B. Элемент C_ik матрицы C имеет вид:

(i = 1, 2, …, n; k = 1, 2, …, n),

т.е. элемент матрицы С, стоящий в i-й строке и k-м столбце, равен сумме произведений соответствующих элементов i-й строки матрицы A и k-го столбца матрицы B.

.

2. Проверить, что определитель δ равен нулю

Справа от определителя приписываются два первых столбца. Со знаком «+» берутся три произведения элементов, стоящих на главной диагонали и двух параллельных ей диагоналях. Со знаком «-» берутся три произведения элементов, стоящих на побочной диагонали и двух параллельных ей диагоналях/

б) Проверить, что определитель Δ равен нулю, выполнив его разложение по 1-й строке.

Определитель Δ равен сумме произведений всех элементов произвольной его строки или столбца на их алгебраические дополнения. Например, для элементов i-й строки такое разложение имеет вид:

где A_ij - алгебраическое дополнение элемента определителя a_ij, равное

Здесь M_ij - минор элемента a_ij, т.е. определитель (n - 1)-го порядка, получающийся после вычеркивания из определителя n-го порядка i-й строки и j-го столбца.

Вычисляем определитель Δ разложением по элементам 1-й строки. Предварительно можно вынести за знак определителя коэффициент пропорциональности элементов 1-й строки, равный 2, а также коэффициент элементов 2-й строки, тоже равный 2.

3. Найти обратную матрицу к матрице А и проверить выполнение равенства А·А^-1 = Е:

.

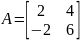Так как определитель Δ матрицы А

то матрица А является невырожденной и для нее существует обратная матрица A^-1. Находим алгебраические дополнения для определителя Δ:

Составляем матрицу из этих алгебраических дополнений и, транспонируя ее, получим присоединенную матрицу (A^*):

.

Вычисляем обратную матрицу A^-1:

.

Проверяем правильность нахождения обратной матрицы:

Так как А·А^-1 = Е, то обратная матрица найдена правильно.

4. Решить систему с помощью вычисления обратной матрицы:

Данная система в матричном виде: AX = B.

Здесь Решение этой системы через обратную матрицу А^-1 имеет вид X = А^-1·B.

В задаче 3 была найдена обратная матрица А^-1, тогда

Отсюда x = 2,3; y = 2,6.

Можно сделать проверку, т.е. подставить найденные значения x и y в исходную систему уравнений.

5. Решить систему уравнений методом исключения переменных (методом Гаусса):

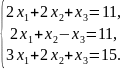
Выполняем прямой ход по методу Гаусса.

Выберем в качестве первого ведущего уравнения - 1-е уравнение системы, и оно в дальнейшем остается без изменения, а в качестве 1-го ведущего неизвестного - x₁.

Исключаем неизвестную x₁ из 2-го и 3-го уравнений системы с помощью 1-го уравнения. Для этого из 1-го уравнения вычитаем 2-е уравнение, получим x₂ + 2x₃ = 0. Затем 1-е уравнение умножаем на 3, а 3-е уравнение умножаем на 2 и вычитаем из 1-го уравнения 3-е уравнение; получим 2x₂ + x₃ = 3.

Выписываем систему:

Неизвестная x₁ исключена. Первый шаг выполнен. Теперь за ведущее уравнение берется 2-е уравнение, и оно в дальнейшем не изменяется, а за ведущую неизвестную принимается x₂.

Исключаем из 3-го уравнения переменную x₂. Для этого 2-е уравнение умножаем на 2 и вычитаем из него 3-е уравнение системы; получим 3x₃ = -3.

Выписываем систему:

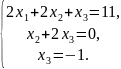
Прямой ход метода Гаусса закончен. Обратным ходом получаем:

x₃ = -1,

x₂ = -2x₃ = -2·(-1) = 2,

2x₁ = 11 - 2x₂ - x₃ = 11 - 2 · 2 - (-1) = 8, x₁ = 4.

Ответ: x₁ = 4, x₂ = 2, x₃ = -1.