Методические указания и контрольные задания
по дисциплине
Математика
Правила оформления и зачета контрольных работ
Контрольная работа должна быть оформлена в соответствии с настоящими правилами. Работы, выполненные без соблюдения этих правил, не засчитываются и возвращаются студенту для переработки.
Контрольная работа оформляется в отдельной тетради или на листах формата А4 чернилами любого цвета, кроме красного, или в машинописном виде. Предусмотреть поля для замечаний рецензента.
На обложке тетради (титульном листе) указать институт, название дисциплины (математика), № варианта (m = , n = , см. ниже), ФИО студента, номер группы, ФИО рецензента. В конце работы поставить датy ее выполнения и расписаться.
Номер варианта контрольной работы определяется по номеру студента в журнальном списке или по номеру зачетной книжки следующим образом.
Формирование исходных данных к задачам
При отсутствии зачетной книжки
Для всех вариантов условия задач одинаковы, однако числовые данные зависят от номера студента в списке журнала учета посещаемости и успеваемости.
Числовые данные своего варианта (параметры m и n) определяются из таблицы 1. Эти два числа (m и n) нужно подставить в условия задач.
Таблица 1 (выбор параметров m и n)
№ в журнале учета посещаемости |
m |
n |
№ в журнале учета посещаемости |
m |
n |
1 |
3 |
2 |
16 |
4 |
3 |
2 |
5 |
1 |
17 |
2 |
5 |
3 |
1 |
4 |
18 |
3 |
5 |
4 |
3 |
5 |
19 |
5 |
4 |
5 |
2 |
3 |
20 |
2 |
1 |
6 |
4 |
1 |
21 |
3 |
4 |
7 |
2 |
5 |
22 |
1 |
5 |
8 |
1 |
2 |
23 |
3 |
2 |
9 |
5 |
4 |
24 |
4 |
4 |
10 |
3 |
3 |
25 |
3 |
2 |
11 |
3 |
2 |
26 |
2 |
4 |
12 |
5 |
2 |
27 |
3 |
1 |
13 |
1 |
3 |
28 |
2 |
5 |
14 |
3 |
4 |
29 |
4 |
1 |
15 |
2 |
2 |
30 |
1 |
4 |
При наличии зачетной книжки
Для того, чтобы получить свои числовые данные, необходимо взять две последние цифры своего номера зачетной книжки (А – предпоследняя цифра, В - последняя) и выбрать из таблицы 1 параметр m, а из таблицы 2 – параметр n. Эти два числа m и n и нужно подставить в условия задач.
Таблица 1 (выбор параметра m)
А |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
m |
4 |
3 |
5 |
1 |
3 |
2 |
4 |
2 |
1 |
5 |
Таблица 2 (выбор параметра n)
В |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
n |
3 |
2 |
1 |
4 |
5 |
3 |
1 |
5 |
2 |
4 |
Например, если номер зачетной книжки студента заканчивается на …37, то А=3, В=7, и из таблиц находим, что m=1, n=5. Полученные m=1 и n=5 подставляются в условия всех задач работы этого студента (его вариант: 15).
Если номер зачетной книжки состоит из одной цифры, то надо взять А=В. Например, если номер зачетной книжки студента имеет всего лишь одну цифру 7, то А=В=7, и из таблиц находим, что m=2, n=5.
Решения задач располагать в порядке возрастания номеров. Условия задач следует переписать.
При решении задач обосновать каждый этап решения, представляя промежуточные вычисления, объясняя выполненные действия и используемые формулы. Решение каждой задачи должно доводиться до окончательного ответа, которого требует условие.
Задания контрольной работы
1. Выполнить действия с матрицами:
а)
; б)
.
2. Проверить, что определитель Δ равен нулю
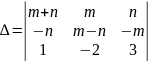
а) по «правилу треугольника»; б) разложением по 1-й строке
3. Найти обратную матрицу к матрице А и проверить выполнение равенства А·А-1 = Е:
.
4. Решить систему с помощью вычисления обратной матрицы:
5. Решить систему методом Гаусса
6. Найти пределы функций:
а)
б)
7. Найти производные функций:
а)
б)
в)
г)
8. Найти интегралы и в пункте а) результат проверить дифференцированием:
а)
б)
