Глава 3. Побудова перспективних масштабів

§ 10. Загальні поняття про перспективні масштаби

Для побудови зображень на картині реальних предметів навколишнього світу треба знати ще і метричні властивості цих предметів, тобто їхні розміри й окремі частини, відстані між ними в просторі. При цьому можливо побудова в перспективі зображення просторової фігури по заданих розмірах (пряма задача) і визначення натуральних розмірів предмета по його зображенню на картині (зворотна задача). Задачі, у яких для рішення ставляться метричні умови (взаємне розташування і величина просторових фігур), називаються метричними.

Одним з основних шляхів рішення метричних задач є застосування масштабу, що дозволяє установити співвідношення між натуральними і перспективними лінійними розмірами зображуваних предметів. Для цього необхідно знать одиницю довжини лінійного масштабу картини в натурі, тобто масштаб картини.

Помітимо, що при тому самому охопленні простору масштаб картини різний, якщо міняється величина її рамки (мал. 46).

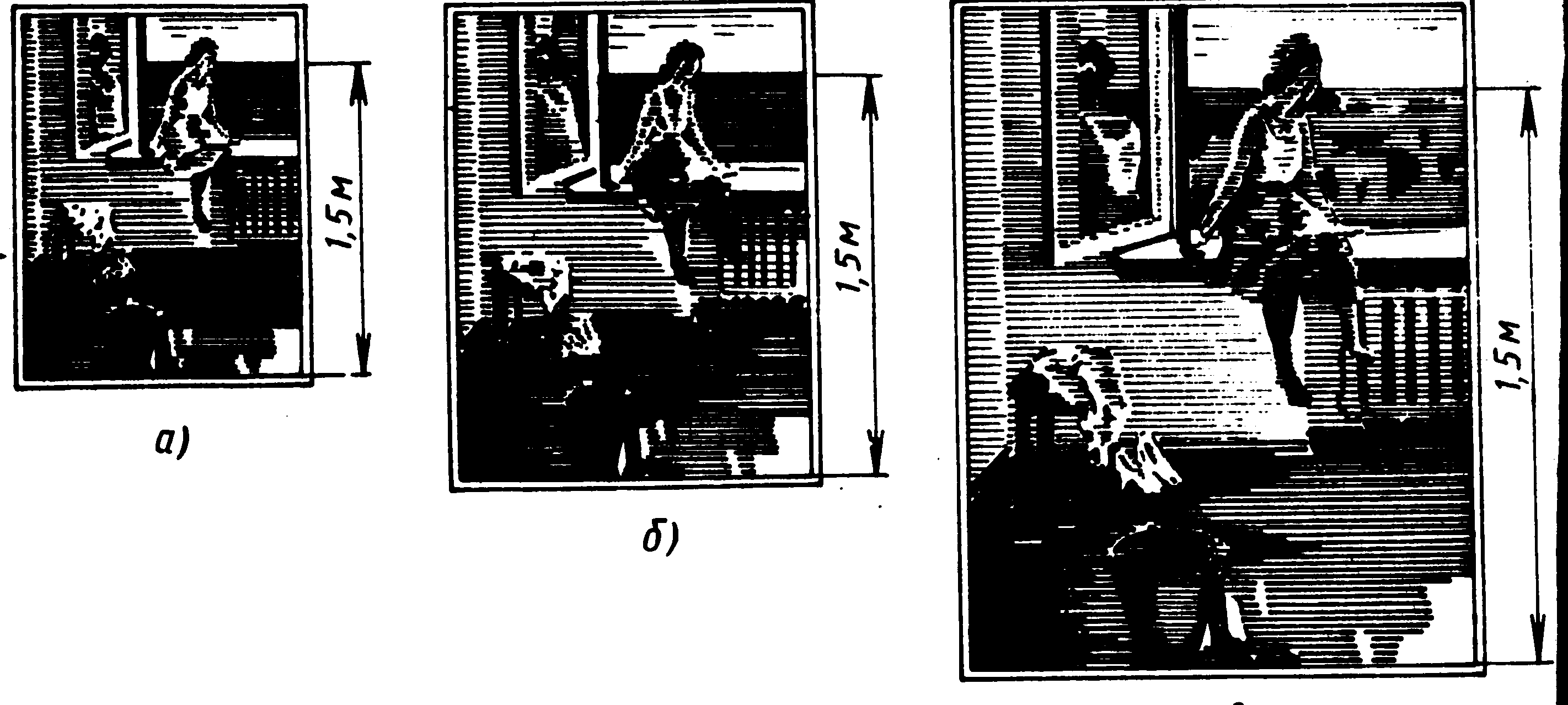
Мал. 46

Але при тому самому розмірі картини масштаб її може бути різним, якщо міняється охоплення простору, обмеженого рамкою картини. При зображенні портрета людини масштаб картини вибирають близьким до натурального (мал. 47, а). При зображенні фігури людини в інтер'єрі (мал. 47, б) використовують масштаб зменшення, тому що рамка картини тих же розмірів повинна охопити більший простір. На малюнку 47, в охоплення простору значно збільшується, отже, одиниця виміру на картині, що визначає її масштаб, також зменшується.

а) б) в)

Мал. 47

Розміри рамки картини і її положення (вертикальне чи горизонтальне) художник вибирає відповідно до задуму і змісту композиції. А це обумовлює вибір масштабу картини. Отже, натуральний масштаб картини — це відношення одиниці виміру на картині до одиниці виміру в натурі. Одиницю довжини на картині визначають або задають різними способами.

Якщо на картині задана відстань лінії обрію від основи картини і відома висота точки зору, то одиницю виміру на картині визначають з їхнього співвідношення. Відомо, що висота точки зору відповідає відстані від основи картини до лінії обрію (лінія обрію в натурі знаходиться на рівні точки зору). Отже, при висоті точки зору Ss =1,5 м і відстані від основи картини до лінії обрію, рівному 60 мм, натуральна лінійна одиниця 1 м буде відповідати одиниці виміру 40 мм на картині.

Для визначення на картині відстаней між точками фігури і її розмірів будують перспективний масштаб відповідно до напрямку вимірюваних відрізків. Для цього виділяють три головних напрямки в предметному просторі:

1) напрямок глибини, тобто прямих, розташованих перпендикулярно до площини картини;

2) напрямок широти, тобто прямих, розташованих паралельно основі картини;

3) напрямок висоти, тобто прямих, розташованих перпендикулярно до предметної площини.

Відповідно до головних напрямків будують перспективні масштаби: глибин, широт, висот.

§ 11. Масштаб глибин

М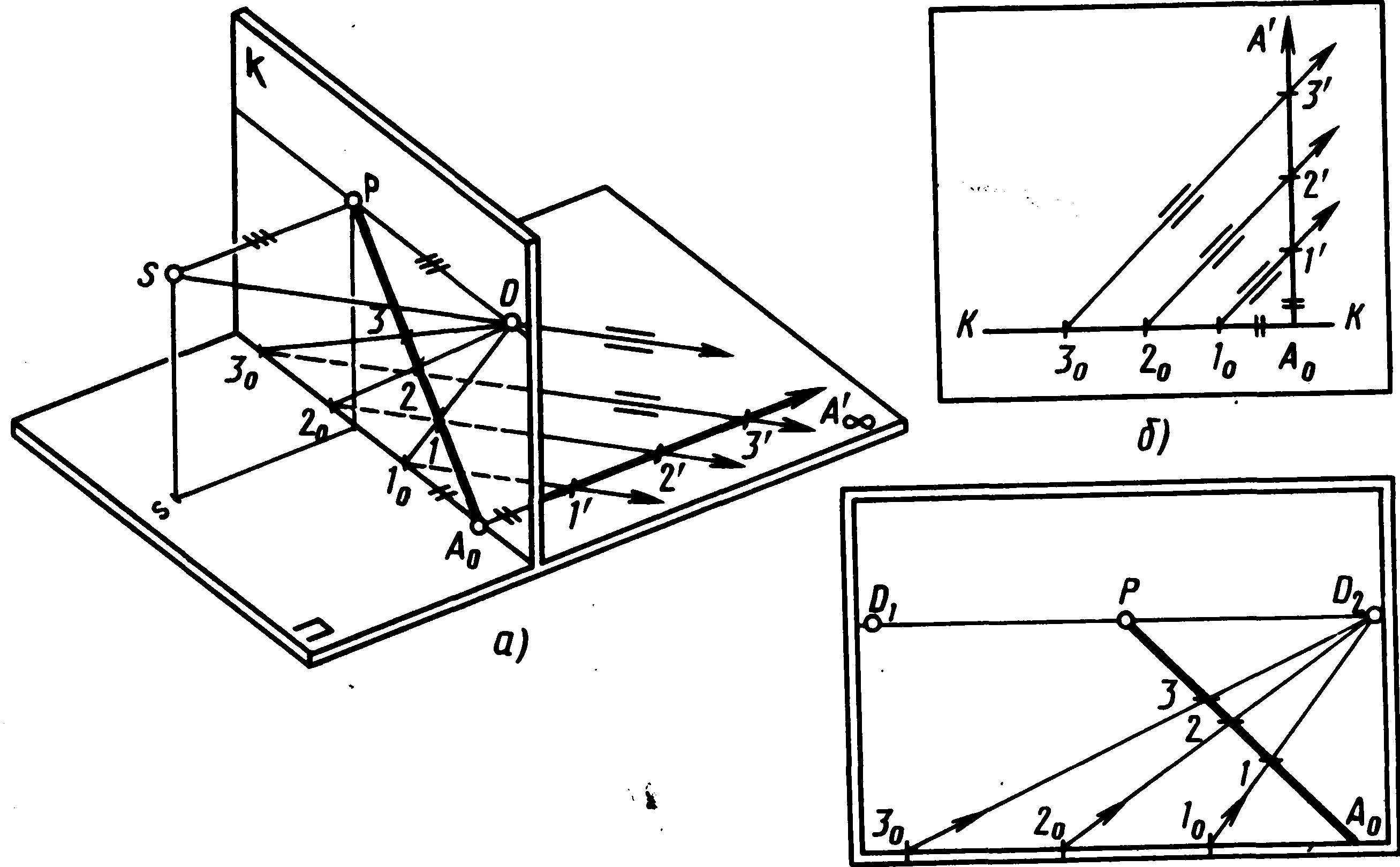 асштаб, побудований на прямій, яка перпендикулярна до площини картини, називається масштабом глибин. Розглянемо його побудову на апараті, що проектує (мал. 48, а). Спочатку задають у предметній площині глибинну пряму А_о . Вона перпендикулярна до площини картини. На основі картини від точки А_о відзначають розподілами 1₀, 2₀, 3₀ натуральні відрізки в масштабі картини. Потім переносять (відкладають циркулем) ці відрізки з основи картини на задану пряму А_о і з'єднують однойменні точки паралельними прямими . На малюнку 48,б показана геометрична побудова.

Мал. 48

Помітимо, що трикутники 1₀А₀ 1^/, 2₀ А₀2^/, 3₀А₀3^/ прямокутні (А_о ┴ kk), рівнобедрені (катети рівні за побудовою) і подібні (паралельні схожі сторони).

Далі знаходять перспективне зображення глибинної прямої і пучка рівнобіжних прямих. Перспективою заданої прямої буде відрізок А_оР, тому що граничною точкою глибинної прямої є головна точка. Перспективу паралельних прямих будують за допомогою їхньої загальної граничної точки. Направивши промінь зору SD паралельно даним прямим, знаходять точку його перетинання з лінією обрію. Точка D буде точкою сходу пучка паралельних прямих. Тоді лінії переносу 1₀ – D, 2₀ – D, 3₀ – D в перетинанні з прямої А_оР відзначать точки 1, 2, 3, які визначать перспективні відрізки Ао—1, 1—2, 2—3, рівні по довжині відрізкам, заданим на основі картини.

Розглянемо трикутник SРD, що утворився в площині обрію. Він подібний трикутнику 1_оА_о1^/ тому що в них паралельні схожі сторони. Отже, він прямокутний і рівнобедрений, а катети SР і РD рівні між собою. Звідси випливає, що при побудові масштабу глибин точкою сходу ліній переносу є дистанційна точка, що знаходиться на лінії обрію і відстоїть від головної точки Р на зорову відстань SР. Як бачимо, побудова масштабу глибин зв'язана з якщо точку, яка відділяє

положенням точки зору щодо картини. При побудові перспективних зображень дистанційна відстань є одним з елементів картини і задається автором-художником.

Л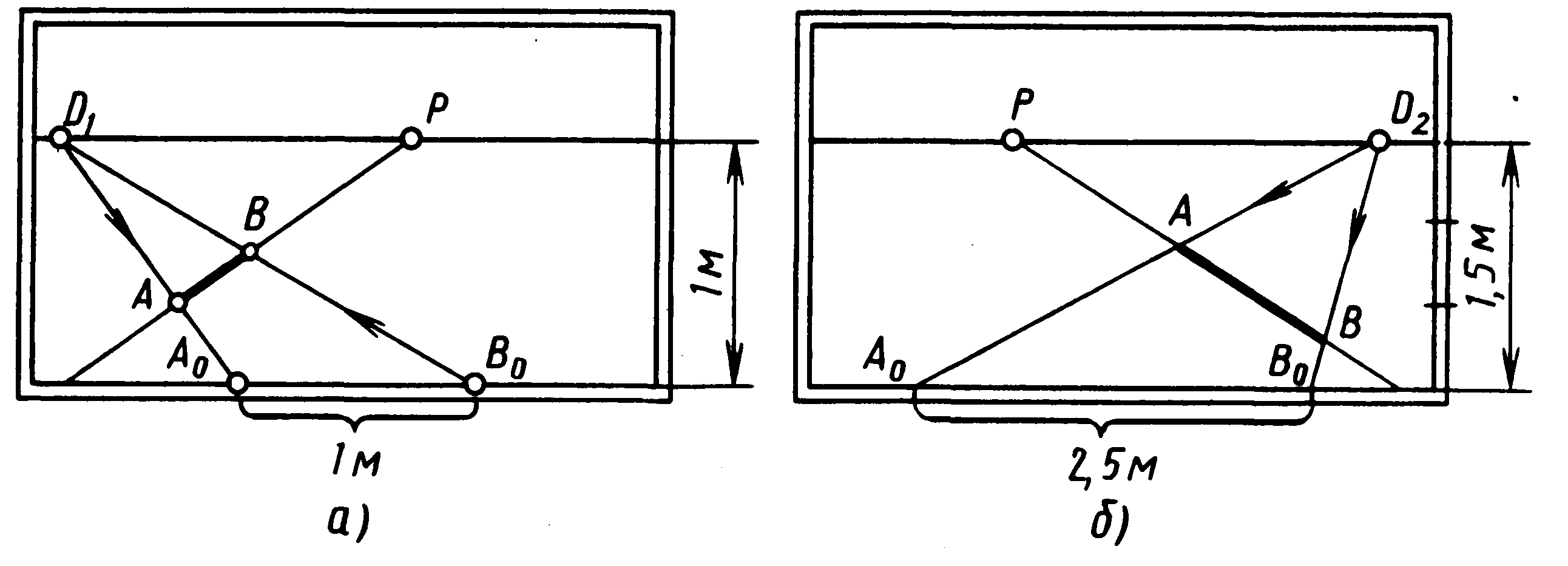 інії переносу, що складають з основою картини кут 45°, проводять на предметній площині в двох різних напрямках. Тому на лінії обрію відзначають дві дистанційні точки D₁ і D₂, розташовані по різні сторони і на рівній відстані від головної точки Р (мал. 48, в). Якщо пряма знаходиться ліворуч від лінії головного вертикала, то користуються лівою дистанційною точкою D₁ (мал. 49, а), а якщо пряма праворуч, те застосовують точку D₂ (мал. 49, б).

Мал. 49

Для побудови перспективного масштабу глибин натуральний масштаб, заданий на основі картини, переносять на глибинну пряму за допомогою ліній переносу, які мають точку сходу — дистанційну.

Якщо потрібно побудувати в перспективному масштабі на глибинній прямій відрізок від заданої точки А, то через неї і дистанційну точку проводять лінію переносу до перетинання з основою картини (див. мал. 49, а). Від отриманої точки А_о на основі картини відкладають натуральну одиницю масштабу (наприклад, А_оВ_о=1 м) і проводять другу лінію переносу, яка відзначить на заданій прямій точку В, що обмежує відрізок АВ, рівний 1 м у масштабі картини.

Для визначення натуральної величини глибинного відрізка, зображеного на картині, проводять через його кінці і дистанційну точку лінії переносу до перетинання з основою картини.

Винесена величина відповідно до натурального масштабу картини визначить розмір відрізка.

На малюнку 49,б заданий відрізок АВ складає 2,5 м у масштабі даної картини.

Д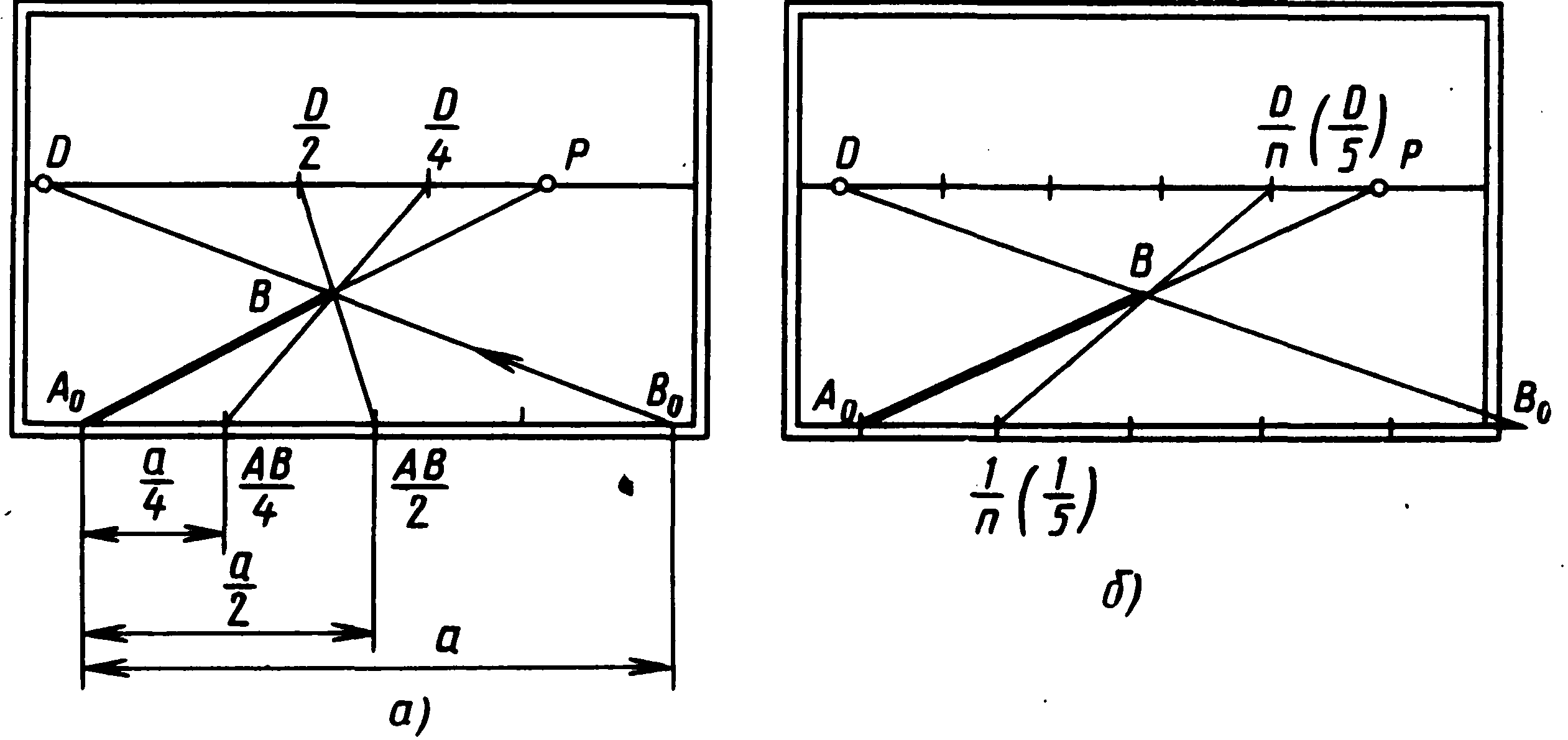 рібна дистанційна точка. У практиці побудови перспективних зображень зорова дистанційна відстань часта значно перевершує лінійні розміри картини, унаслідок чого дистанційна крапка виходить за її межі. Щоб перспективне зображення предмета відповідало зоровому враженню, відстань точки зору від картини повинна дорівнюватися 1,5—2 діаметрам поля ясного зору людини (див. § 3). При цієї відстані дистанційна точка і виходить за межі картини, що ускладнює побудову і робить його менш точним. У таких випадках для побудови масштабу глибин користаються так названою дрібною дистанційною точкою.

Мал. 50

Розглянемо застосування дрібної дистанційної точки. На картині (мал. 50, а) дана глибинна пряма А_оР і за допомогою дистанційної точки D побудований перспективний відрізок А_оВ=а, Помітимо, що цей же відрізок можна побудувати на картині, якщо з'єднати середину відрізка натурального масштабу із точкою , яка поділяє навпіл дистанційну відстань РD, або четверту частину відрізка натурального масштабу , з'єднати з точкою і далі зменшити масштаб у п разів.

Якщо для побудови масштабу глибин не можна скористуватися повною дистанційною відстанню, то задають деяку його частину, що знаходиться в межах картини. Відзначивши відповідну дрібну дистанційну точку на лінії обрію, її використовують як точку сходу ліній переносу для розподілів натурального масштабу, одиниця якого складає цю ж частину одиниці заданого масштабу.

Помітимо, що на картині (мал.50,б) при дрібній дистанційній точці одержують перспективний масштаб глибин, одиниця якого відповідає повній одиниці спочатку заданого натурального масштабу. При такій побудові кожен розподіл повного натурального масштабу при переносі на перспективний масштаб відзначає відрізок, що відповідає п одиницям натурального.

§ 12. МАСШТАБ ШИРОТ

М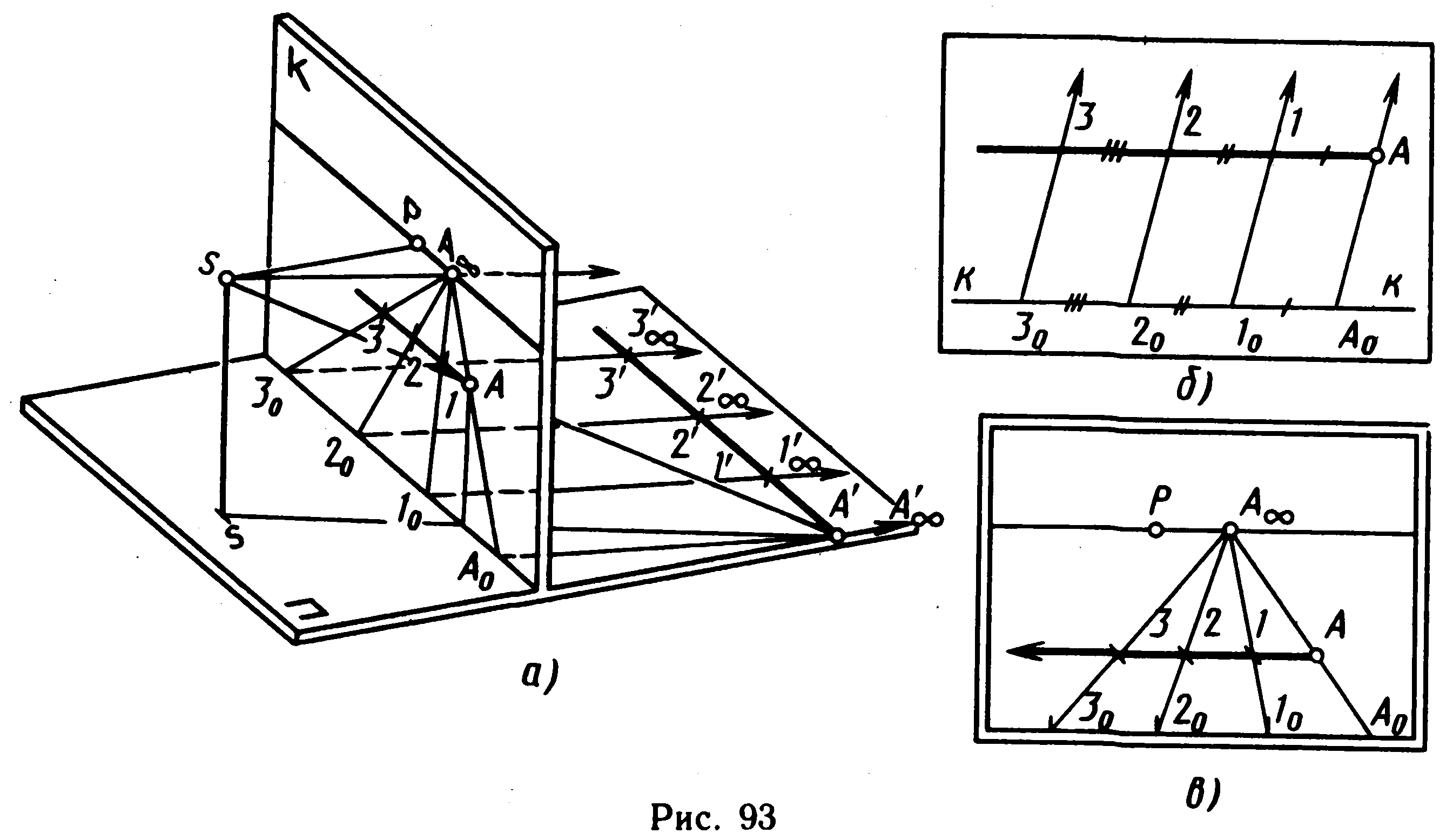 асштаб, побудований на прямій, паралельної основі картини, називається масштабом широт. Розглянемо його побудову на апараті, що проектує, (мал. 51, а). Задамо в предметній площині пряму, паралельну основі картини, із точкою А'. Потрібно відкласти від точки А' на прямої довільні натуральні відрізки А_о—1_о, 1_о—2_о і 2_о— 3_о, які задані на основі картини. Спочатку переносять їх на дану пряму за допомогою паралельних ліній переносу в напрямку А_о-А^/. (Геометричні побудови показані на малюнку 51, б.) Потім будують на картині перспективу точки А' і заданої прямої. Визначають положення точки сходу ліній переносу , направлюючи паралельно їм промінь зору до перетинання з обрієм. З'єднавши відзначені розподіли на основі картини з точкою сходу , одержують точки перетинання А, 1, 2, 3 ліній переносу з заданої прямої. Отримані відрізки А—1, 1—2, 2—3 є перспективним зображенням натуральних відрізків, заданих на основі картини (мал. 51, в). Мал. 51

П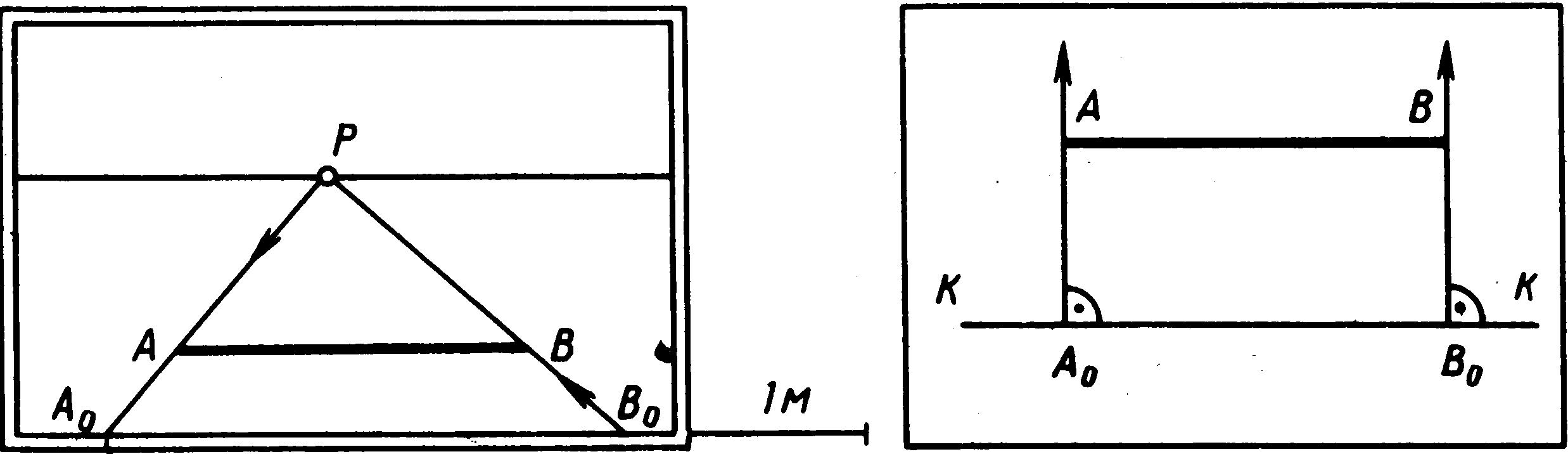 омітимо, що точка сходу ліній переносу не може бути узята довільно, якщо задані натуральний масштаб на основі картини А_о—1_о, 1_о—2_о, 2_о—3_о і початкова точка А на даній прямій. Точка сходу – це гранична точка прямої, що з'єднує початкові точки натурального А₀ і перспективного А масштабів.

а) б)

Мал. 52

Для побудови перспективного масштабу широт натуральний масштаб з основи картини переносять на задану пряму за допомогою ліній переносу, довільно задавши їхню точку сходу на обрії або використовуючи головну точку.

На картині (мал. 52, а) паралельно її основі задана пряма з точкою А на ній. Потрібно від точки А відкласти відрізок, рівний по величині 3 м у масштабі картини. Для цього проводять через точку А глибинну (або довільну) пряму з граничною точкою Р до перетинання з основою картини в точці А₀. (Аналогічна геометрична побудова дана на малюнку 52, б.)

На основі картини від точки А_о відкладають 3 м у масштабі картини і його кінець В₀ з'єднують із точкою Р. Отримана точка В перетинання лінії переносу з даної прямої визначить відрізок АВ, рівний у перспективі натуральному – величині А_оВ_о в масштабі картини.

Д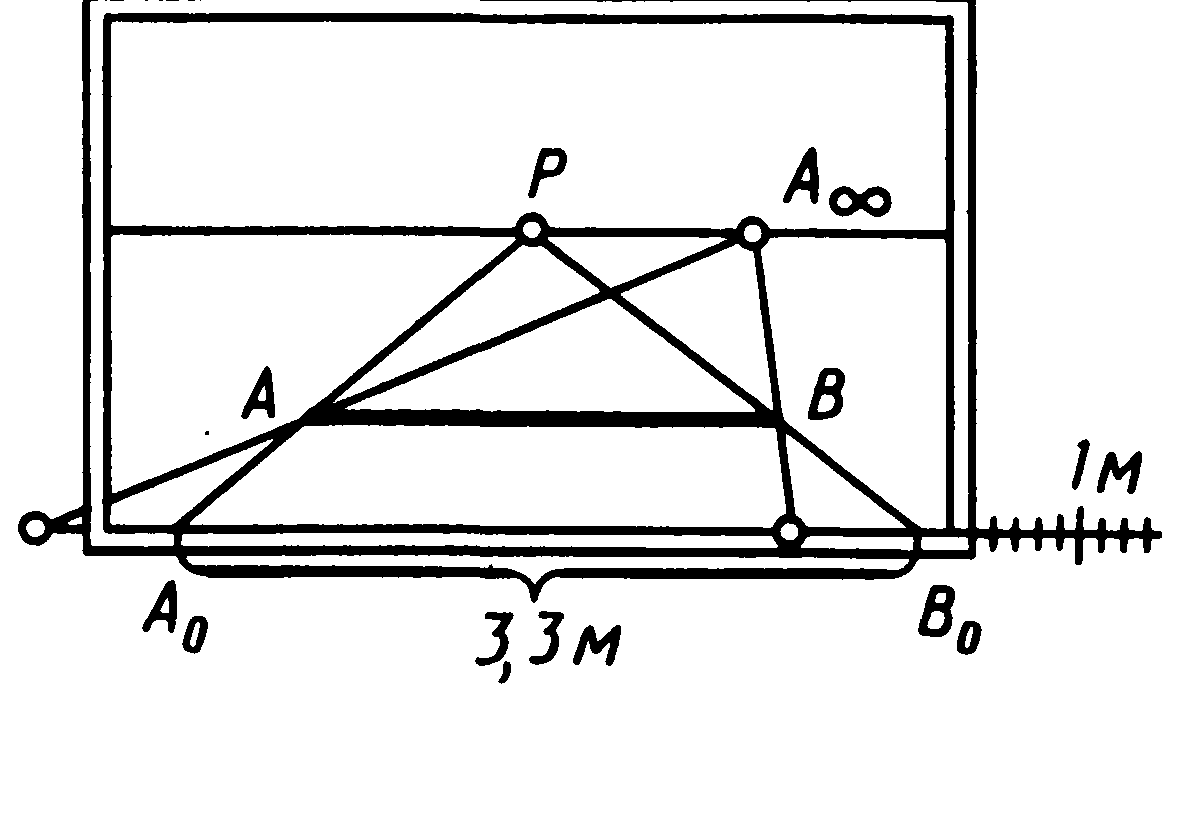 ля визначення натуральної величини відрізка, розташованого паралельно основі картини, беруть на лінії обрію головну або будь-яку точку сходу ліній переносу. Через неї і кінці заданого відрізка проводять лінії переносу, що у перетинанні з основою картини визначать натуральну величину відрізка, який шукали.

На картині (мал. 53) заданий відрізок АВ, розташований паралельно основі картини. Потрібно визначити його натуральну величину.

Мал. 53

Для цього через головну точку Р або будь-яку точку сходу на лінії обрію і кінці відрізка А і В проводять лінії переносу до перетинання з основою картини. Відрізок А_оВ_о на основі картини є його натуральною величиною й у даному прикладі буде відповідати 3,3 м натурального масштабу.