§ 8. Сліди прямої

П ри рішенні ряду позиційних задач виникає необхідність будувати сліди прямої. У перспективі слідами прямої є точки її перетинання з предметною і картинною площинами. Точка перетинання прямої з предметною площиною називається її предметним слідом. Точка перетинання прямої з картинною площиною називається її картинним слідом.

Мал. 28 Мал. 29

Для побудови слідів прямої її укладають у площину. Потім будують лінії перетинання допоміжної площини з предметною і картинною. Продовжуючи пряму до перетинання з отриманими лініями, знаходять точки перетинання прямої з картинною (картинний слід) і з предметною (предметний слід) площинами.

На малюнку 28 показана побудова у перспективі предметного А_П і картинного А_К слідів спадної прямої А_КА_П загального положення.

Мал.30 Мал. 31

На малюнку 29 дана побудова в перспективі предметного А_П і картинного А_К слідів висхідної прямої загального положення. У даному прикладі картинний слід висхідної прямої розташований на продовженні картини під її основою. Аналогічно будують сліди в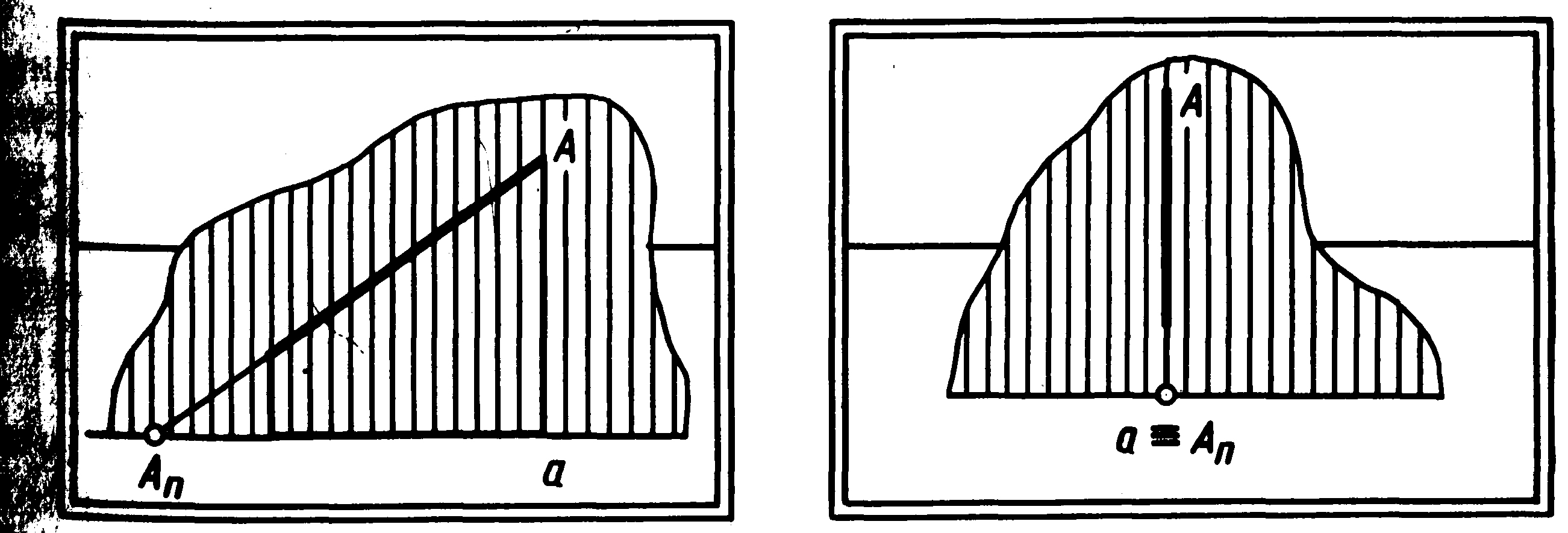 исхідної (мал. 30) і спадної (мал. 31) прямих особливого положення. Помітимо, що прямі часного положення, як правило, мають тільки один слід.

Мал. 32 Мал. 33

Т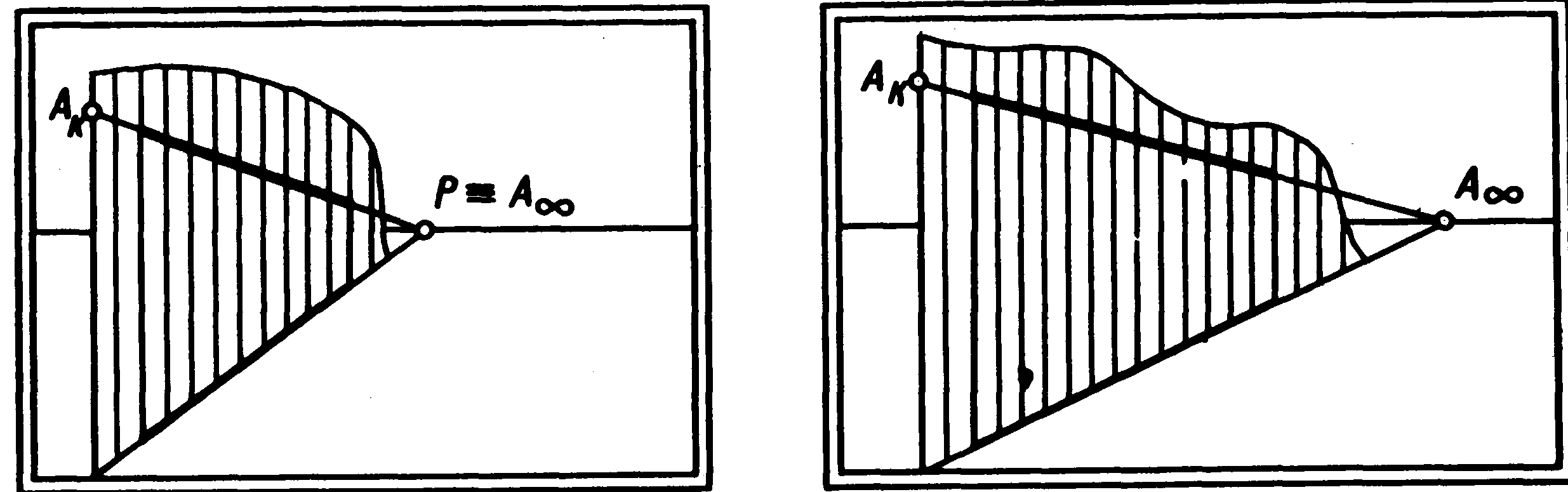 ак, фронтальна (мал. 32) і вертикальна (мал. 33) прямі мають тільки предметний слід А_П. Глибинна (мал. 34) і горизонтальна прямі, розташовані під довільним кутом до картинної площині (мал. 35), мають тільки картинний слід А_К. Горизонтальна пряма, розташована паралельно предметній і картинній площинам, слідів не має.

Мал. 34 Мал. 35

§ 9. Взаємне положення прямих

В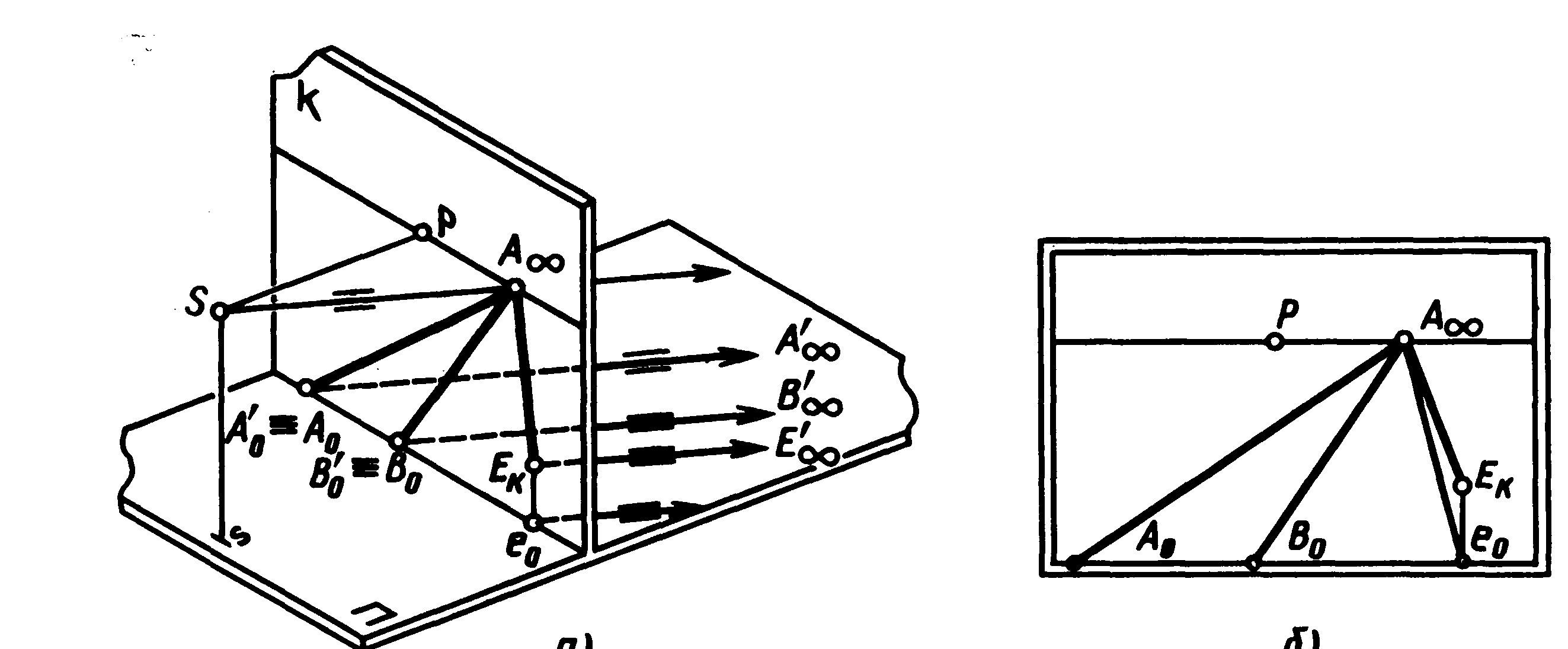 ідносно один одного прямі можуть бути паралельними, пересічними, перехресними. Важливо знати і уміти визначати ознаки взаємного положення двох прямих, зображених на картині. Це дасть можливість вирішувати прямі (будувати перспективу взаємного положення прямих) і зворотні (визначати їхнє взаємне положення по зображенню на картині) задачі.

Мал. 36

Паралельні прямі. Найбільше часто зустрічаються паралельні прямі. З практики спостережливої перспективи відомо, що паралельні прямі здаються нам сходяться в одній точці (залізнична полотнина, шосейна дорога, вулиця і т.д.). Для обґрунтування такого явища звернемося до апарата, що проектує.

Задамо на апараті, що проектує, (мал. 36, а) пучок паралельних прямих ( ),довільно розташованих у предметній площині і їй паралельної ( ). Побудуємо перспективу кожної прямої. Для цього скористаємося наявними точками А₀, В₀, Е₀, тобто картинними слідами цих прямих. Визначимо граничну точку кожної прямої (див. мал. 17). Помітимо, що для всіх заданих прямих вона буде загальна - , тому що визначається тим самим променем зору S , проведеним паралельно їм до перетинання з лінією обрію.

Отже, довільно спрямовані горизонтальні паралельні прямі на картині зображуються пучком прямих, що сходяться в одній граничній точці. Загальна гранична точка довільно розташованих горизонтальних паралельних прямих знаходиться на лінії обрію і називається точкою сходу. (Закон точки сходу горизонтальних прямих.)

Помітимо, що на картині (мал. 36, б) для паралельних прямих( ), що лежать у предметній площині і їй паралельної ( ), точка сходу може лежати в будь-якім місці на лінії обрію в залежності від їхнього напрямку.

Якщо паралельні прямі глибинні, тобто розташовані перпендикулярно картинної площини, то точкою сходу їх буде головна точка Р (мал. 37).

О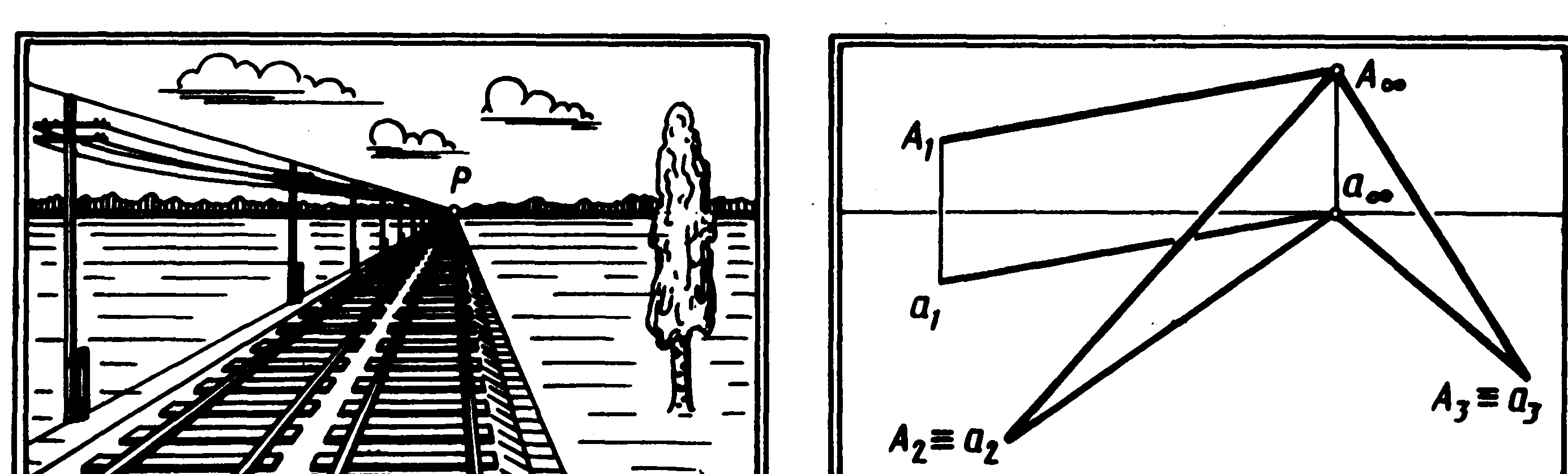 тже, точкою сходу глибинних паралельних прямих є головна точка картини. (Закон точки сходу пучка глибинних прямих.)

Мал. 37 Мал. 38

Розглянемо перспективу висхідних паралельних прямих загального положення (мал. 38). Якщо висхідні прямі паралельні, то їхні проекції на предметну площину також між собою паралельні. Проекції паралельних прямих лежать у предметній площині, тому будуть мати загальну граничну точку — точку сходу на лінії обрію. Тоді точка сходу висхідних паралельних прямих буде лежати на перпендикулярі, проведеному до лінії обрію через точку сходу їхніх проекцій.

Отже, висхідні паралельні прямі загального положення мають точку сходу, яка розташована над лінією обрію в довільному місці і лежить на одному перпендикулярі з точкою сходу проекцій цих прямих. (Закон точки сходу пучка висхідних прямих загального положення.)

А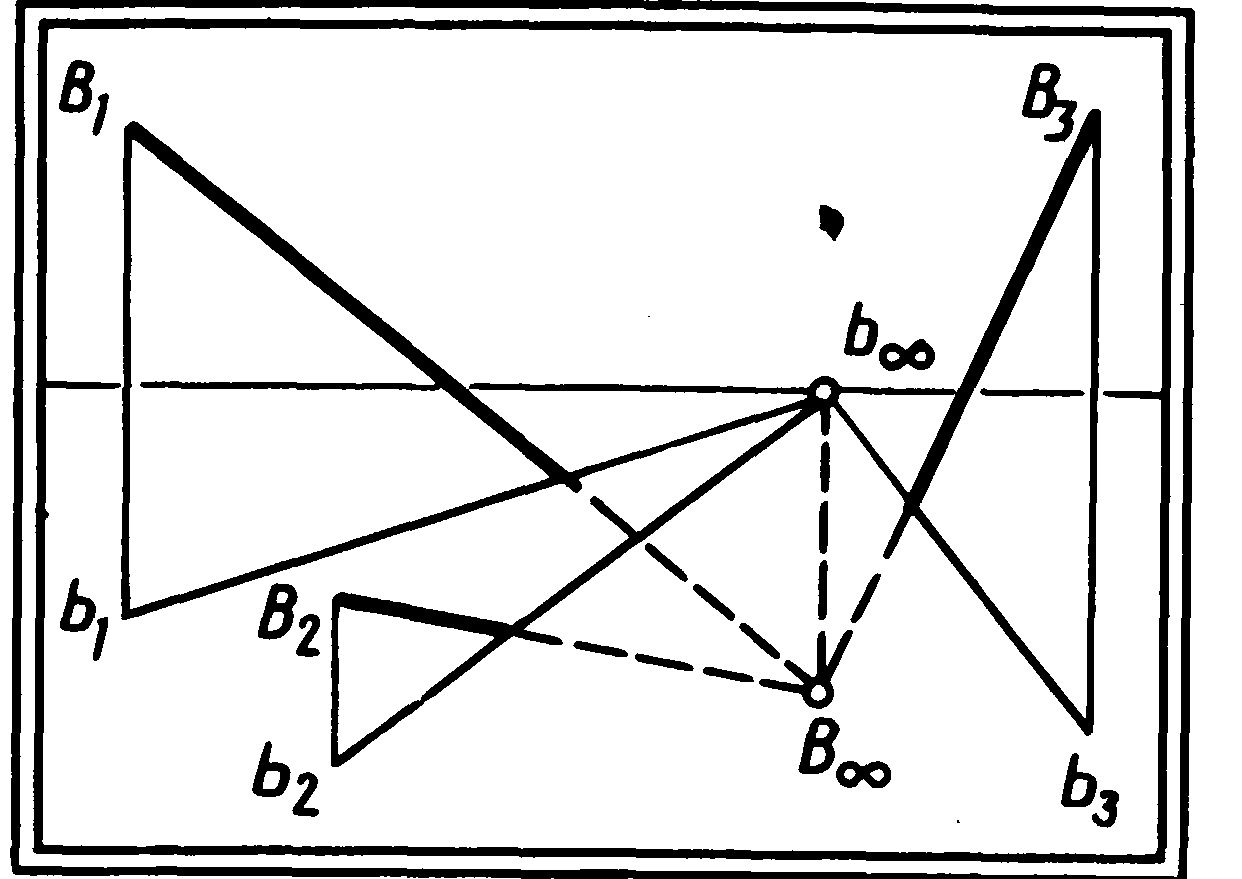 налогічно будують зображення спадних паралельних прямих. Різниця лише в тім, що їхня точка сходу буде розташована в довільному місці під лінією обрію (мал. 39).

Отже, східні паралельні прямі загального положення мають точку сходу, яка розташована під лінією обрію в довільному місці і лежить на одному перпендикулярі з точкою сходу їхніх проекцій. (Закон точки сходу пучка спадних прямих загального положення.)

Мал. 39

Т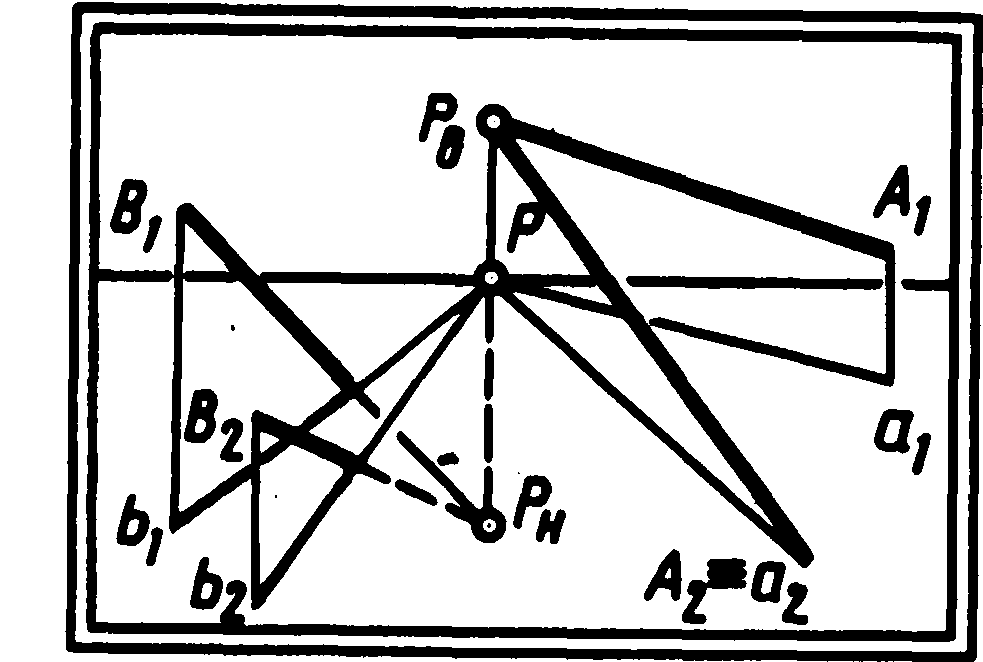 аким чином, ознакою паралельності прямих загального положення, зображених на картині, є розташування на одному перпендикулярі точок сходу прямих і їхніх проекцій. При цьому точка сходу проекцій паралельних прямих повинна лежати на лінії обрію.

На малюнку 40 зображені дві пари висхідних (А₁Р_{В і} А₂Р_В) і спадних (В₁Р_Н і В₂Р_Н) паралельних прямих особливого положення. На основі загального правила їхні точки сходу лежать на одному перпендикулярі до лінії обрію. Помітимо, що в даному випадку перпендикуляром є лінія головного вертикала.

Мал. 40

Отже, висхідні паралельні прямі особливого положення мають точку сходу на лінії головного вертикала над обрієм, а їхніх проекцій — у головній точці. (Закон точки сходу пучка висхідних прямих особливого положення.)

Східні паралельні прямі особливого положення мають точку сходу на лінії головного вертикала під обрієм, а їхніх проекцій – у головній точці картини. (Закон точки сходу пучка спадних прямих особливого положення.)

Особливі ознаки мають прямі часного положення, які розташовані паралельно картині. Прямі, паралельні картині, зображуються на ній паралельними.

Якщо паралельні прямі фронтальні, то в перспективі вони залишаються паралельними між собою, а їхні проекції паралельні основі картини, оскільки ці прямі і їхні проекції не мають граничних точок (мал. 41).

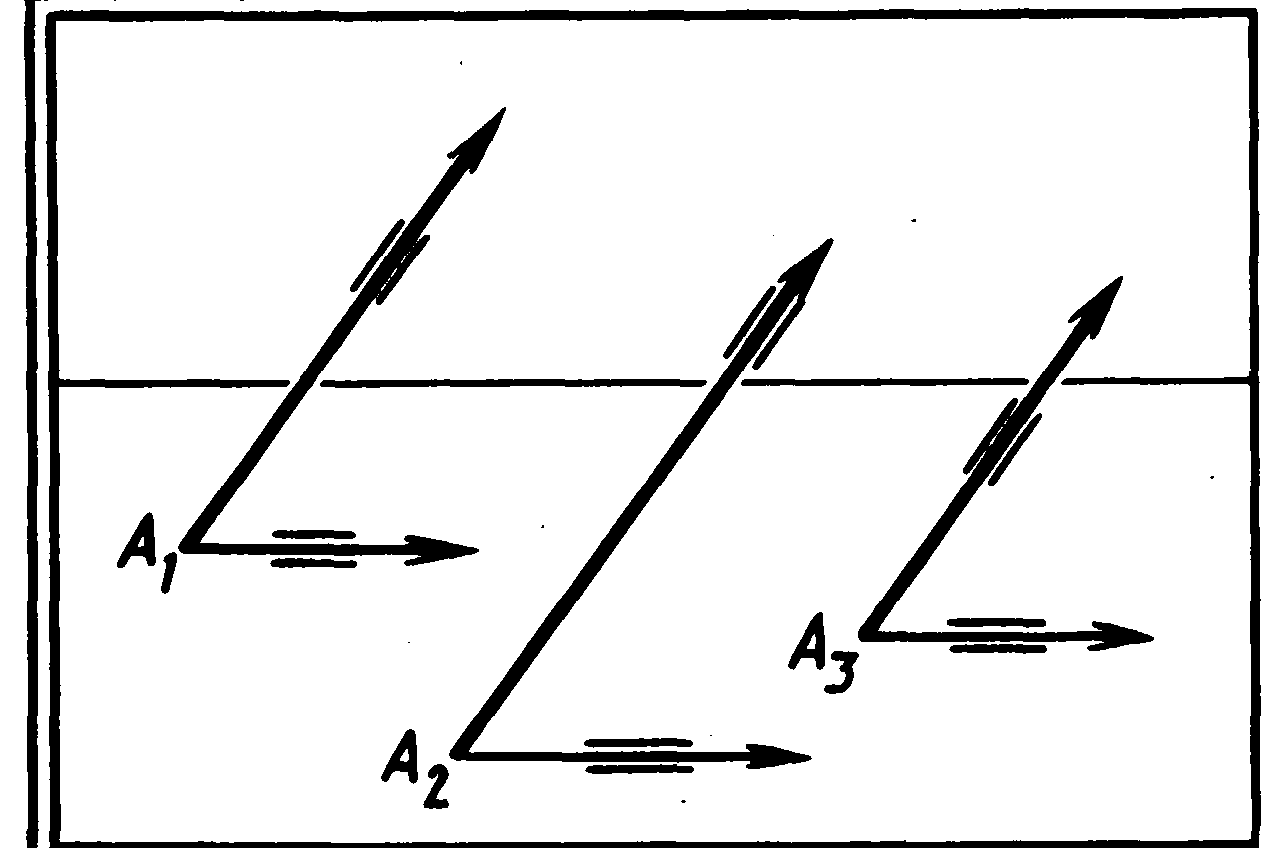
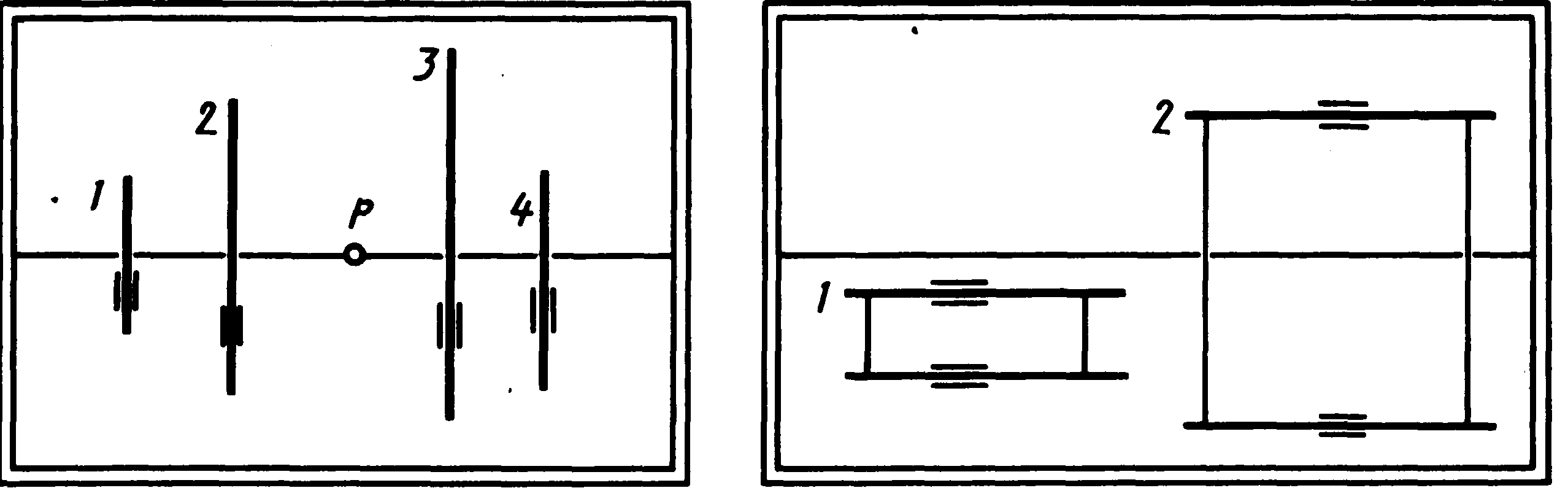
Мал. 41 Мал. 42 Мал. 43

Якщо паралельні прямі вертикальні, то в перспективі вони залишаються вертикальним і паралельними між собою, тому що вони не мають граничної точки (мал. 42).

Якщо паралельні прямі горизонтальні (паралельні картинній і предметній площинам), то в перспективі вони і їхні проекції залишаються паралельними між собою і основі картини (мал. 43).

Пересічні прямі. Задамо на картині дві пересічні в точці А прямі (мал. 44). Тоді проекції цих прямих на предметну площину перетинаються в точці а. Причому точка а — проекція точки перетинання А даних прямих. Точки А і а знаходяться на одному перпендикулярі. Якщо на картині точки перетинання двох прямих і їхніх проекцій лежать на одному перпендикулярі, то дані прямі перетинаються між собою в дійсності.

Перехресні прямі. Задамо на картині дві перехресні прямі (мал. 45). Якщо прямі схрещуються, то вони не можуть бути паралельними і не повинні мати загальної точки. Отже, на картині точки перетинання прямих і їхніх проекцій не повинні лежати на одному перпендикулярі. І дійсно, якщо на картині перпендикуляр до предметної площини, проведений із точки а₁ перетинання проекцій двох прямих, перетинає їх у двох різних точках А₁ і А₂, то дані прямі схрещуються між собою в дійсності. На картині точка, що здається перетинанням двох прямих, є зображенням двох різних точок В₁ і В₂, які лежать на перехресних прямих. Обидві точки розташовані на одному промені зору і тому на картині збігаються.

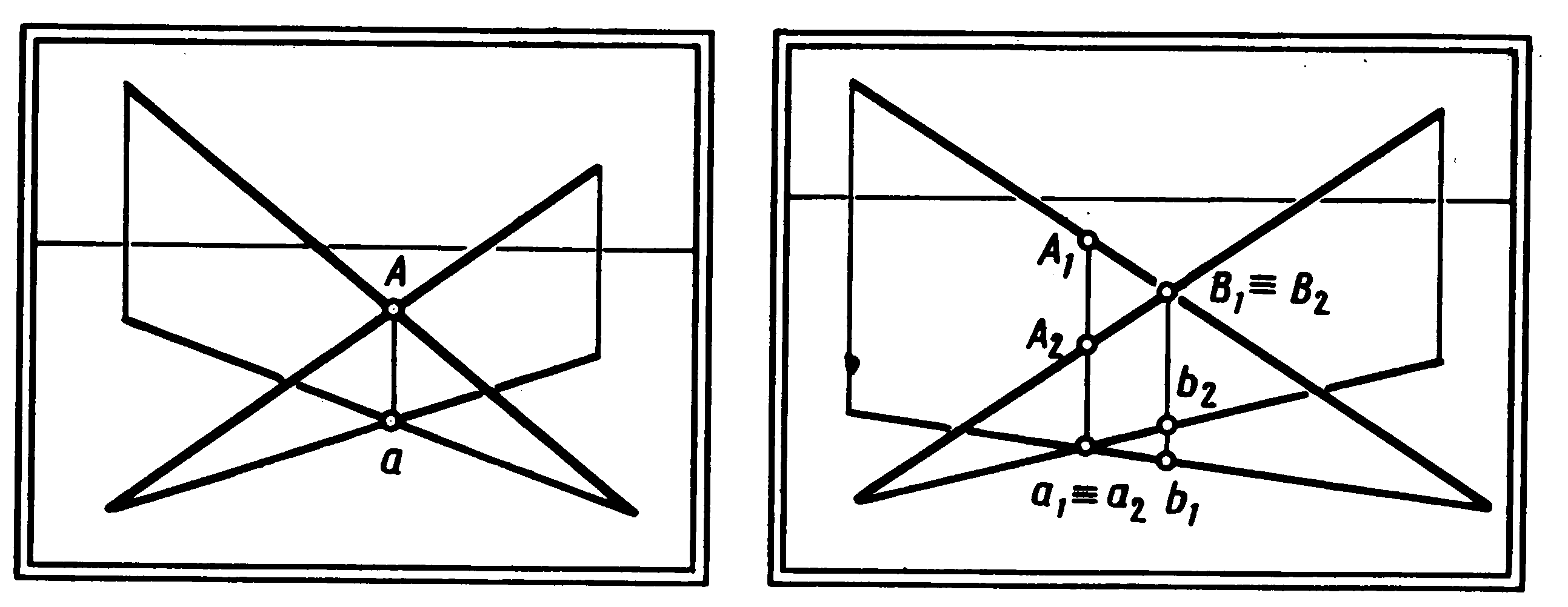
Мал. 44 Мал. 45

Помітимо, що основи цих точок, що злилися на картині, по-різному вилучені від основи картини (b₁ ближче, b₂ далі). Це вказує на різне віддалення від картини відповідних їм точок на заданих прямих (точка В₁ ближче до глядача, а точка В₂ далі). Прямі схрещуються в дійсності, якщо на картині точка перетинання проекцій даних прямих є проекцією двох різних точок.