Способи побудови зображень окружності в перспективі

Відомо кілька способів побудови окружності в перспективі. Основним, найбільш простим і зручним, є спосіб описаного квадрата. Сутність його полягає в тім, що спочатку будують у перспективі квадрат, потім у нього вписують окружність, визначивши вісім точок — середини сторін квадрата і перетинання окружності з його діагоналями. Цей спосіб зручно застосовувати при зображенні в перспективі окружності невеликих розмірів.

Виконаємо таку побудова окружності, що лежить у предметній площині. Для цього задають натуральну величину окружності, вписаної в квадрат і сполученої з площиною картини. Для спрощення побудови одну зі сторін квадрата сполучають з основою картини (мал. 73).

Побудову виконують у наступній послідовності. Спочатку будують перспективу квадрата і відзначають на ньому чотири точки, що лежать на серединах його сторін. В окружності ці точки будуть кінцями вертикального (1—3) і горизонтального (2—4) діаметрів. Для їхнього знаходження проводять глибинні прямі, що відповідають напрямкам вертикальних сторін квадрата і діаметра окружності. Через правий (чи лівий) кут квадрата проводять його діагональ із точкою сходу D₁ (чи D₂).

П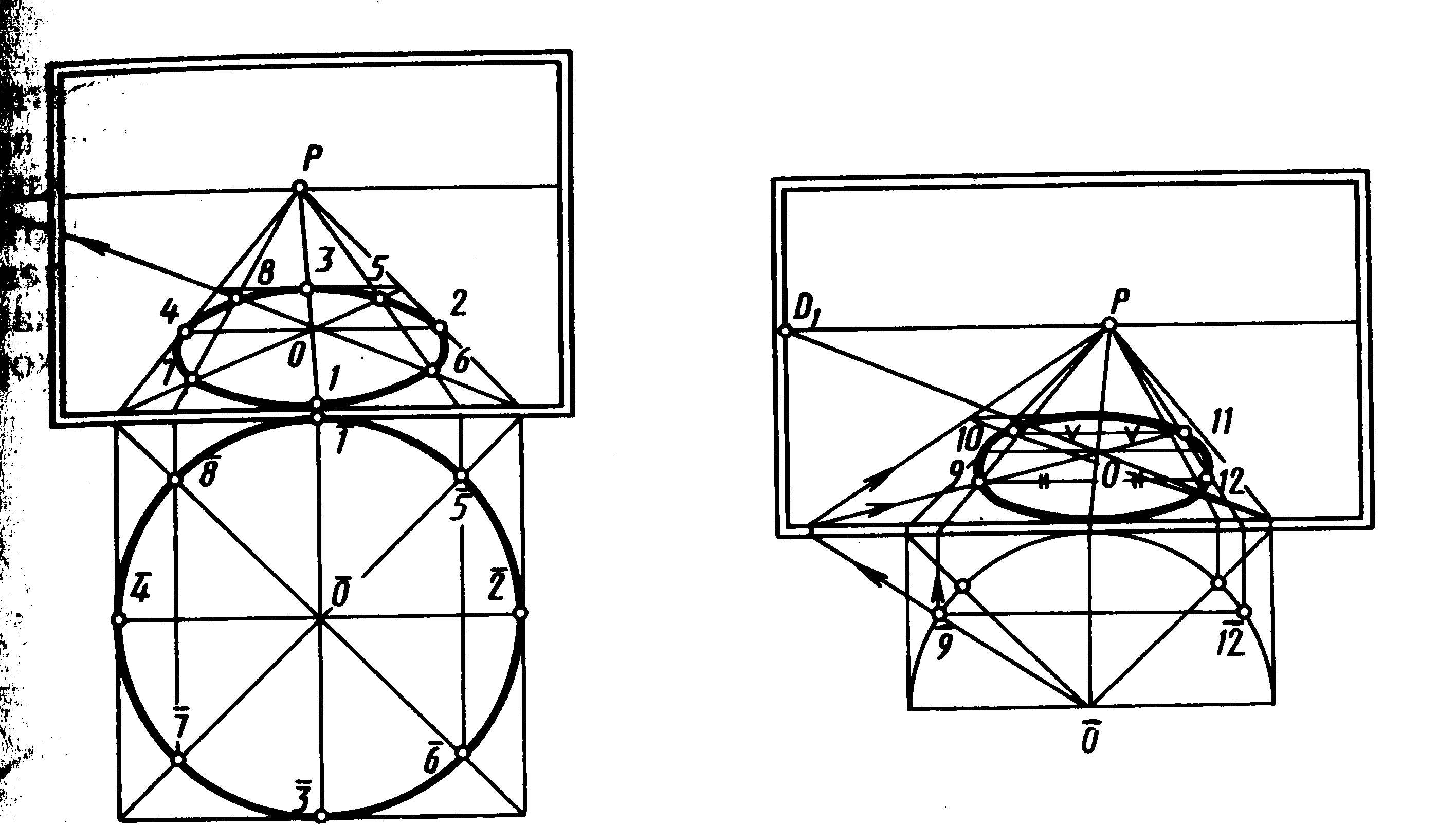 еретинання діагоналі з лівою стороною квадрата визначить у перспективі його вершину і далеку сторону. Перетинання діагоналі з глибинною прямою — зображенням вертикального діаметра окружності — визначить її центр і горизонтальний діаметр. Кінці діаметрів окружності лежать на серединах сторін квадрата. У перспективі вони визначать чотири точки еліпса: 1, 2, 3, 4.

Мал. 73 Мал. 74 Потім будують ще чотири точки перетинання діагоналей квадрата з окружністю (5, 6, 7, 8). Для цього в сполученому фронтальному положенні квадрата проводять дві допоміжні прямі через точки 5 і 6, 7 і 8, паралельні вертикальному діаметру окружності. У перспективі вони будуть глибинними прямими, що у перетинанні з діагоналями квадрата визначать ще чотири точки еліпса: 5, 6, 7, 8. З'єднавши послідовно всі добудовані точки плавною лінією, одержують зображення окружності в перспективі — еліпс.

При використанні способу описаного квадрата можна спростити побудову. Для цього в сполученому положенні з картиною будують половину квадрата (мал. 74) або його чверть і вписують в них відповідно половину або чверть окружності.

Якщо відстань між деякими точками дуже велико, то застосовують проміжні, додаткові точки. Їх знаходять у перетинанні окружності з допоміжною прямою, що проходить через центр О. Так (див. мал. 74) на окружності знайдена точка 9 у перетині глибинної прямої з допоміжною, яка проведена через центр еліпса. У такий же спосіб побудована точка 10. Визначивши у перспективі точки 9 і 10, можна побудувати симетрично їм ще пару точок: 11 і 12, відклавши на горизонтальних прямих відповідну половину хорди.

При побудові в перспективі зображення великої окружності для забезпечення максимальної точності знаходять до 16 точок й більш. Для цього застосовують спосіб побудови парних точок, зв'язаних діагоналлю квадрата, описаного біля даної окружності.

Задамо на картині (мал. 75) перспективу квадрата з центром О і відзначимо точки еліпса, що лежать на його сторонах і діагоналях. В даному прикладі для побудови використане не сполучене положення окружності з картиною, а фронтальна площина, побудована при далекій стороні квадрата. Помітимо, що тут побудована лише чверть окружності і її радіус відповідає половині сторони квадрата в перспективі. На фронтальній окружності відзначають точки 9 і 10, які симетричні щодо діагоналі. Потім через відзначені точки проводять горизонтальні і вертикальні лінії (тут вони штрихові), які будуть перетинати діагоналі квадрата.

Мал. 75 Мал. 76 Мал. 77

Далі цю ж побудову виконують у перспективі. Відповідно до положення вертикальних прямих будують глибинні прямі з точкою сходу Р. А через точки перетинання їх з діагоналями проводять горизонтальні прямі, що визначать у перспективі положення точок 9 і 10. На малюнку відзначені дві пари точок лівої половини квадрата. Симетрично їм праворуч можна побудувати, як у попередньому прикладі, ще дві пари точок, відклавши відрізки хорд.

Якщо окружність розташована у вертикальній площині, то застосовують той же спосіб описаного квадрата і виконують побудови, аналогічні попереднім прикладам. Так, спочатку на картині (мал. 76) у вертикальній площині будують перспективу квадрата з заданою стороною А_оВ­_к і визначають чотири точки еліпса, які лежать на його сторонах (1, 2, 3, 4). Потім знаходять точки перетинання діагоналей квадрата з окружністю, для чого використовують допоміжні прямі, що на картині є глибинними. Сполучений квадрат, у який вписана окружність (у даному прикладі узята його 1/4 частина), розташовують збоку при картинному сліді А_оВ_к площини. Для побудови точок, розташованих на діагоналях, застосовують фронтальне положення квадрата, заданого при ближній чи далекій його стороні. Помітимо, що можна будувати тільки 1/8 частину окружності, як це показано на малюнку 77.