Для побудови картинного сліду площини q проводять граничну пряму ра . Потім через точку Qо паралельно граничній прямій ра проводять картинний слід QоQк допоміжної площини q.

Помітимо, що лінії переносу повинні лежати в площині Q, а отже, масштабна точка повинна знаходитися на граничній прямій РА цієї площини. Для визначення положення масштабної точки М будують на картині сполучену точку зору шляхом обертання точки зору S навколо граничної прямої РА . Аналогічно попереднім прикладам сполучена точка зору буде знаходитися на перпендикулярі, проведеному з головної точки Р к граничної прямої РА даної площини на відстані Р = РD. Тоді масштабну точку М визначають на граничної прямої РА як кінець відрізка А М == А .

Далі через кінець А і масштабну точку М проводять лінію переносу, що у перетинанні з картинним слідом Q_оQ_к допоміжної площини визначить точку відліку О_к. Відклавши від точки О_к відрізки натурального масштабу на картинному сліді площини (О_к —1_к, 1_к—2_к, 2_к—3_к), переносять їх на задану пряму лініями переносу з масштабною точкою сходу М . Отримані відрізки А—1, 1—2, 2—3, 3—4 на висхідній прямій загального положення є перспективним зображенням натуральних відрізків, заданих у масштабі картини.

Для побудови перспективного масштабу на прямій загального положення її укладають у площину, що проектує, перпендикулярну картині. Потім відкладають відрізки натурального масштабу на картинному сліді площини і переносять їх на задану пряму лініями переносу з масштабною точкою сходу, розташованої на граничній прямій цій площині.

§ 15. Розподіл відрізка

Перспективний масштаб може бути використаний у розв’язанні метричних задач, прикладом яких є розподіл відрізка на рівні або пропорційні частини.

Приклад. На картині (мал. 62, а) заданий у предметній площині довільно розташований відрізок АВ. Потрібно розділити його на чотири рівні частини. Для рішення задачі застосовують геометричний спосіб, заснований на теоремі Фалеса (мал. 62, б). Через кінець А (чи В) проводять горизонтальну пряму і на ній відкладають чотири довільних, але рівних між собою відрізка. Останній розподіл (4) з'єднують з кінцем відрізка В прямій, що продовжують до перетинання з лінією обрію, і відзначають на ній крапку сходу В_∞ лінії переносу. Потім через всі інші р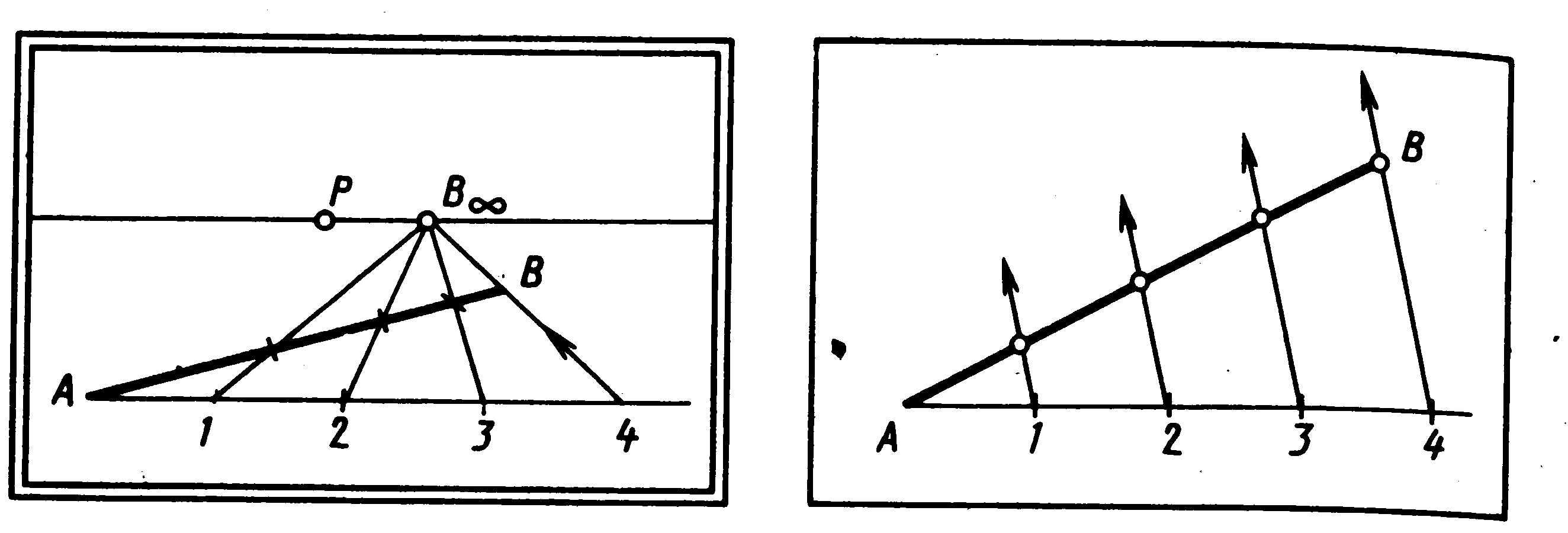 озподіли 1, 2, 3 проводять лінії переносу, що розділять відрізок АВ при його перетинанні на чотири рівні частини.

а) б)

Мал. 62

Питання для самоконтролю

1. Що називається масштабом картини?

2. Що називається масштабом глибин, широт, висот?

3. Що є дрібна дистанційна точка? У яких випадках її застосовують на картині?

4. Які направлення прямої можливі при вільному масштабі?

5. Що називають масштабною точкою? У яких випадках її застосовують?

6. Яку метричну задачу Ви знаєте? Як вона розв’язується?

Глава 4. Побудова в перспективі пласких фігур і геометричних тіл

Навколишні предмети мають в основі форму найпростіших геометричних тіл, пласкогранних (куб, паралелепіпед, призма, піраміда) і круглих (циліндр, конус, куля, різні види тора). Їхні поверхні можуть бути нахилені до предметної і картинної площин під різним кутом, по-різному розташовані відносно один одного.

При зображенні на картині предметів різної форми з’являється необхідність будувати в перспективі плоскі кути (у тому числі прямі), найпростіші фігури і геометричні тіла. Усі ці побудови виконують за визначеними правилами перспективи, які розглянуті в цій главі.