§ 14. Перспективний масштаб на довільно спрямованої прямої

Прямі щодо картинної і предметної площині можуть бути розташовані довільно. Масштаб, побудований на довільно спрямованої прямої, називається масштабом у вільному напрямку.

Відомі чотири випадки довільного розташування прямої в предметному просторі: горизонтальне, фронтальне, особливого і загального положення. Розглянемо побудову перспективного масштабу на кожній з цих прямих.

П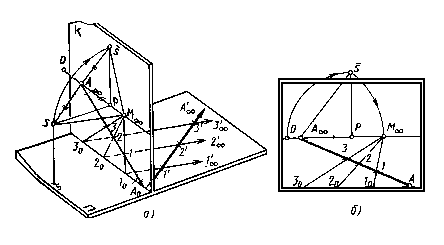 ерспективний масштаб на вільно направленій горизонтальній прямий. Обґрунтування способу побудови цього масштабу та процес його одержання розглянемо на апараті, що проектує (мал. 57, а). Для спрощення доказу розглянемо приклад, коли пряма А_о лежить у предметній площині і довільно спрямована до основи картини. Потрібно побудувати на ній перспективний масштаб.

Мал. 57

Спочатку на основі картини, починаючи від точки А₀, відкладають відрізки А_о—1_о, 1_о—2_о, 2_о - 3_о натурального масштабу. Потім переносять циркулем відрізки з основи картини на задану пряму А₀А ^/ і з'єднують відзначені розподіли прямими 1_о—1', 2_о—2', З_о—3'. Ці прямі паралельні, оскільки між ними лежать за побудовою попарно рівні відрізки. Звідси випливає, що трикутники 1_оА_о1', 2_оА_о 2', 3_оА_о 3', із загальним кутом при вершині А_о будуть рівнобедреними і подібними.

Далі будують перспективне зображення прямої А₀А ^/ і пучка паралельних прямих, заданих у предметному просторі. Для цього з точки зору проводять промінь SA паралельно заданої прямої і промінь SМ паралельно пучку прямих. У перетинанні цих променів з картиною на лінії обрію знаходять граничну A точку прямої А₀А ^/ і точку сходу ліній переносу. Після цього будують на картині перспективу прямої А₀А і пучка паралельних прямих 1₀ М , 2₀ М , 3₀ М . Дані лінії переносу в перетинанні з прямої А₀А відзначать точки розподілів 1, 2, 3 перспективного масштабу.

Помітимо, що трикутник SA М , що утворився в площині обрію, подібний трикутнику 1_оА_о1' (унаслідок паралельності схожих сторін) і тому є рівнобедреним (SA = A М ).

Зробимо перетворення, повернувши трикутник A М навколо лінії обрію і сполучивши його з площиною картини. Точка зору S при сполученні з картиною буде знаходитися на перпендикулярі, проведеному з головної точки Р к лінії обрію, і на відстані SР= Р. У сполученому рівнобедреному трикутнику сторона A М = М . Це дозволяє знайти на картині точку сходу М ліній переносу.

Виконаємо викладені вище побудови на картині без апарата, що проектує, (мал. 57, б). Для цього задають картину з її елементами. У предметній площині картини зображують довільно спрямовану пряму А₀А . Побудова перспективного масштабу на цій прямій виконують у такій послідовності.

Спочатку відкладають на основі картини від точки А_о задані відрізки натурального масштабу А_о—1_о, 1_о—2_о, 2_о - 3_о. Потім на перпендикулярі, проведеному з головної точки картини до лінії обрію, відзначають сполучену точку зору , відклавши Р =РD. Далі на лінії обрію відкладають відрізок A М = А (як рівні сторони рівнобедреного трикутника A М ) і визначають масштабну точку.

Масштабна точка — це точка сходу ліній переносу для побудови масштабу на довільно спрямованій прямій. Користаючись масштабною точкою М , за допомогою ліній переносу 1₀ М , 2₀ М , 3₀ М переносять заданий натуральний масштаб з основи картини на пряму А₀А .

Для побудови на картині перспективного масштабу на довільно спрямованій горизонтальній прямій знаходять масштабну точку і за допомогою ліній переносу (паралельних прямих у натурі) переносять відрізки натурального масштабу на задану пряму.

Отже, для побудови перспективного масштабу на вільно спрямованій горизонтальній прямій знаходять масштабну точку, положення якої на лінії обрію для кожної прямої різне.

Перспективний масштаб на довільно спрямованій фронтальній прямій. Щоб показати побудову цього масштабу, звернемося до побудови на картині (мал. 58) без апарата, що проектує.

Для цього задамо фронтальну пряму АВ, укладемо її в площину загального положення Q і побудуємо сліди цієї площини. У фронтальної прямої точка А є одночасно її предметним слідом А_п. Отже, предметний слід площини Q пройде через точку А_п у будь-якому напрямку А_пQ . (З геометрії відомо, що через пряму можна провести незліченну безліч площин.) При перетинанні предметного сліду площини Q з основою картини відзначають точку Q_о, через яку проводять картинний слід площини паралельно даної прямої. (Дві паралельні площини — фронтальна і картинна — перетинаються третій Q, тому лінії їхнього перетинання паралельні.)

Д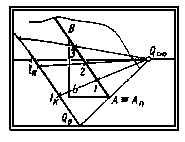 алі відкладають від точки Q_о на картинному сліді відрізки натурального масштабу Q_о—1_к, 1_к—2_к, 2_к—3_к і за допомогою горизонтальних ліній переносу, паралельних предметному сліду площини, і точки сходу переносять їх на фронтальну пряму. Одержані відрізки А—1, /—2, 2—3 є перспективним зображенням заданих відрізків.

Мал. 58

Для побудови перспективного масштабу на довільно направленій фронтальній прямій її укладають у площину загального положення і відкладають відрізки натурального масштабу на її картинному сліді. Потім переносять їх на задану пряму горизонтальними лініями переносу, точкою сходу яких є гранична точка предметного сліду площини.

Перспективний масштаб на прямій особливого положення. Для побудови натурального масштабу на висхідній чи спадній прямій особливого положення звернемося до обґрунтування його на картині (мал. 59) без апарата, що проектує.

Н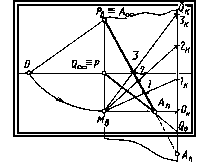 а картині задана висхідна пряма особливого положення А_пР_в із її проекцією А_пР. Потрібно побудувати на ній натуральний масштаб. Для цього укладають її в глибинну площину Q (Q ┴ К), у якої граничної прямої є лінія головного вертикала. Предметний слід Q_оQ глибинної площини пройде через головну точку Р и предметний слід А_п прямої, а картинний слід— через точку Q_о перпендикулярно основі картини (Q_оQ_к ┴ kk).

Мал. 59

Звернемося до малюнка 57, б. Помітимо, що на ньому довільно спрямована пряма А_оА лежить у предметній площині, у якої основа картини є її картинним слідом, а лінія обрію — граничної прямої. У цьому випадку перспективний масштаб переносять на задану пряму за допомогою масштабної точки М .

Аналогічні побудови виконують щодо глибинної площини (див. мал. 59), у якій знаходиться висхідна пряма А_пР_в особливого положення. У цьому прикладі сполучену точку зору заміняють дистанційної (Р = РD). Тоді масштабну точку М_в для висхідної прямої визначають, відклавши відрізок А D == А М_в на граничної прямої (лінії головного вертикала) цієї площини.

Для переносу заданого масштабу на висхідну пряму особливого положення через точку А_п проводять лінію переносу М_вА_п до перетинання з картинним слідом площини і визначають початкову точку відліку О_к. Потім відкладають від неї відрізки натурального масштабу О_к—1_к, 1_к—2_к, 2_к – 3_к, що переносять на задану пряму за допомогою ліній переносу з їх точкою сходу М_в.

Для побудови на картині перспективного масштабу на прямій особливого положення її укладають у глибинну площину й відкладають відрізки натурального масштабу на картинному сліді. Потім переносять їх лініями переносу з масштабною точкою сходу, яка розташована на лінії головного вертикала.

Перспективний масштаб на висхідну чи спадну пряму особливого положення можна перенести по-іншому — способом побудови прямокутного трикутника, винесеного в площину картини.

На картині (мал. 60) заданий відрізок АВ спадної прямої особливого положення. Потрібно визначити його натуральну величину. Помітимо, що відрізок АВ і його проекція аb знаходяться в глибинній площині, яка на картині зображена у вигляді прямокутного трикутника АаВ. Виносимо його в картинну площину. Для визначення натуральної величини горизонтального катета аВ застосовують масштаб глибин, а д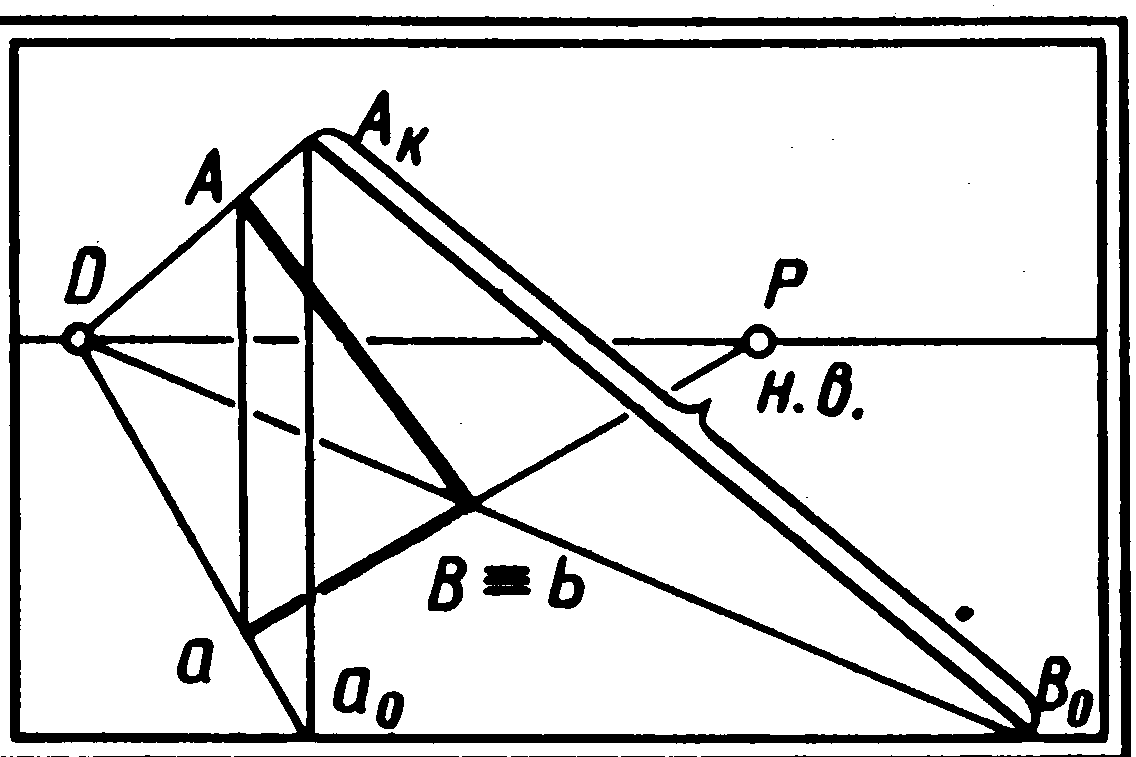 ля вертикального катета Аа— масштаб висот, при цьому з загальною точкою сходу D для ліній переносу. Тоді гіпотенуза А_кВ_о буде натуральною величиною заданого відрізка АВ спадній прямій особливого положення.

Мал. 60

Перспективний масштаб на прямій загального положення. Пряма, на якій необхідно побудувати перспективний масштаб, розташована довільно у предметному просторі і може бути висхідною або спадною. Розглянемо цей випадок тільки на картині без обґрунтування побудов на апараті, що проектує, тому що він аналогічний попереднім прикладам.

Задамо картину з її елементами і довільно спрямовану висхідну пряму АА (мал. 61). Для переносу на неї натурального масштабу виконують побудови в наступної послідовності.

С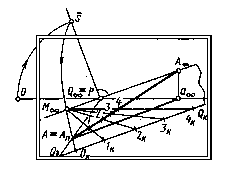 початку проводять через задану пряму допоміжну площину, яка проектується Q, перпендикулярну картині. Тоді предметний слід Q_оQ цієї площини пройде через точку А А_п (предметний слід прямої) і головну точку картини Р як граничну точку глибинної прямої. Потім відзначають точку Q_о перетинання предметного сліду допоміжної площини з основою картини.

Мал. 61