
- •8. Дослідження функції однієї змінної
- •8.1. Умови монотонності та екстремуму
- •Послідовність дій при дослідженні функції на монотонність
- •Послідовність дій при дослідженні функції на екстремум за допомогою першої похідної
- •Послідовність дій при дослідженні функції на екстремум за допомогою другої похідної
- •8.2. Умови опуклості, угнутості, перегину функції
- •Послідовність дій при дослідженні функції на опуклість, угнутість і точки перегину
- •8.3. Схема повного дослідження функції однієї змінної
- •9. Застосування похідної для знаходження границь та екстремальних значень функцій однієї та багатьох змінних
- •9.1. Правило Лопіталя
- •9.2. Знаходження найбільших (найменших) значень функції однієї змінної
- •Послідовність дій при знаходженні найбільшого і найменшого значень функції на відрізку
- •9.3. Екстремум функції двох змінних
- •Контрольні питання зі змістового модуля IV
- •Змістовий модуль II Границі функції
- •Змістовий модуль III Диференціальне числення функцій однієї та багатьох змінних
- •Змістовий модуль IV Застосування похідної
- •Література
- •Предметний покажчик
- •МатематИка для економістів: вища математика
- •83023, М. Донецьк, вул. Щорса, 31.
- •83023, М. Донецьк, вул. Харитонова, 10.
9. Застосування похідної для знаходження границь та екстремальних значень функцій однієї та багатьох змінних
9.1. Правило Лопіталя
Теорема 9.1. |
(правило Лопіталя) Якщо
функції
|
Правило
Лопіталя є досить зручним інструментом
розкриття невизначеностей типів
![]() і
і
 .
.
Приклад 9.1. |
Знайти за правилом Лопіталя наступні границі:
а)
|
Розв’язання.
а)
 ;
;
б)
 .
.
Невизначеність
виду
![]() приводять до
або
,
а потім застосовують правило Лопіталя.
приводять до
або
,
а потім застосовують правило Лопіталя.
Невизначеності
видів
![]() ,
,
![]() ,
,
![]() розкривають попереднім логарифмуванням.
розкривають попереднім логарифмуванням.
9.2. Знаходження найбільших (найменших) значень функції однієї змінної
Якщо
функція
неперервна
на відрізку
![]() ,
то на цьому відрізку
завжди є точки, в яких вона приймає
найбільше
і найменше
значення.
,
то на цьому відрізку
завжди є точки, в яких вона приймає
найбільше
і найменше
значення.
Для визначення найбільшого і найменшого значень функції на відрізку треба знайти критичні точки, які лежать на цьому відрізку (досліджувати критичні точки на екстремум не потрібно), потім знайти значення функції в критичних точках і на кінцях відрізку і серед них вибрати найбільше і найменше значення.
На
рисунку 9.1 представлено графік функції
на
відрізку
,
яка в точці
![]() досягає свого найменшого значення на
відрізку
,
в точці
досягає свого найменшого значення на
відрізку
,
в точці
![]() досягає свого найбільшого значення на
відрізку
.
досягає свого найбільшого значення на
відрізку
.
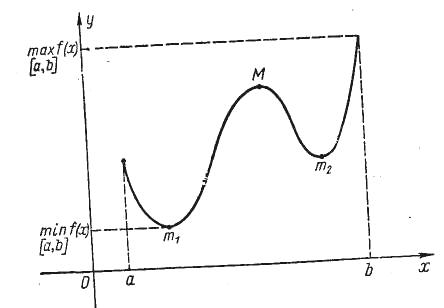
Рисунок 9.1 – Графік функції на відрізку
Зауваження. |
Слід мати на увазі, якщо на відрізку функція має лише одну критичну точку, то саме в цій точці функція досягає найбільшого значення (якщо – точка максимуму) і найменшого значення (якщо – точка мінімуму). |
Послідовність дій при знаходженні найбільшого і найменшого значень функції на відрізку
1) |
Знайти похідну функції . |
2) |
Знайти критичні точки першого роду функції , в яких похідна або не існує. |
3) |
Знайти значення функції в критичних точках і на кінцях відрізку. |
4) |
Обрати найбільше і найменше значення функції. |
Приклад 9.2. |
Знайти
найбільше і найменше значення функції
|
Розв’язання.
1) |
Знайдемо
похідну функції:
|
2) |
Знайдемо
критичні
точки: в точці
|
3) |
Знайдемо значення функції в критичних точках і на кінцях відрізку:
|
4) |
Виберемо найбільше і найменше значення функції:
|

 .
. .
. .
.