
- •8. Дослідження функції однієї змінної
- •8.1. Умови монотонності та екстремуму
- •Послідовність дій при дослідженні функції на монотонність
- •Послідовність дій при дослідженні функції на екстремум за допомогою першої похідної
- •Послідовність дій при дослідженні функції на екстремум за допомогою другої похідної
- •8.2. Умови опуклості, угнутості, перегину функції
- •Послідовність дій при дослідженні функції на опуклість, угнутість і точки перегину
- •8.3. Схема повного дослідження функції однієї змінної
- •9. Застосування похідної для знаходження границь та екстремальних значень функцій однієї та багатьох змінних
- •9.1. Правило Лопіталя
- •9.2. Знаходження найбільших (найменших) значень функції однієї змінної
- •Послідовність дій при знаходженні найбільшого і найменшого значень функції на відрізку
- •9.3. Екстремум функції двох змінних
- •Контрольні питання зі змістового модуля IV
- •Змістовий модуль II Границі функції
- •Змістовий модуль III Диференціальне числення функцій однієї та багатьох змінних
- •Змістовий модуль IV Застосування похідної
- •Література
- •Предметний покажчик
- •МатематИка для економістів: вища математика
- •83023, М. Донецьк, вул. Щорса, 31.
- •83023, М. Донецьк, вул. Харитонова, 10.
Послідовність дій при дослідженні функції на опуклість, угнутість і точки перегину
1) |
Знайти другу похідну функції . |
2) |
Знайти
критичні
точки другого роду функції
,
в яких друга похідна
|
3) |
Визначити знак другої похідної зліва і праворуч від кожної критичної точки. |
4) |
Зробити висновок про інтервали опуклості, угнутість графіка функції і наявність точок перегину. |
5) |
Знайти значення функції в точках перегину. |
Приклад 8.5. |
Знайти
точки перегину, інтервали опуклості
і угнутості графіка функції
|
Розв’язання.
1) |
Знайдемо
першу та
другу похідні:
|
2) |
Знайдемо критичні точки другого роду функції , в яких друга похідна дорівнює нулю 0 або не існує. при , . Це абсциси точок, що “підозрілі” на перегин. |
3) |
Визначимо знак другої похідної зліва і праворуч від кожної критичної точки, представимо в результати в таблиці 8.4: |
Таблиця 8.4
Результати дослідження знаку другої похідної
-
-1
3
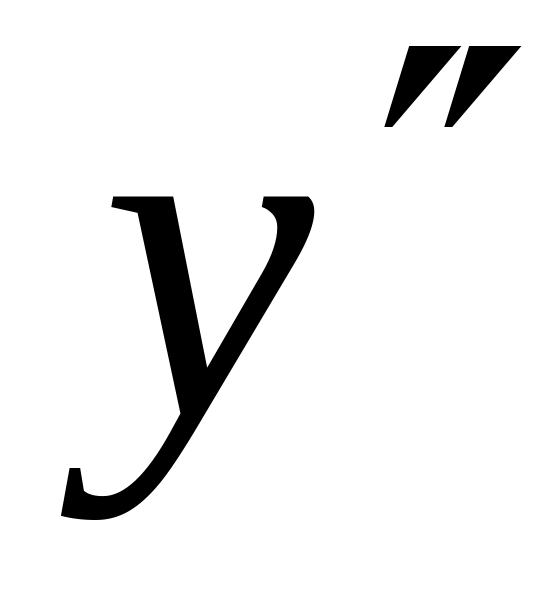
+
0
‑
0
+
графік
угнутий
точка
перегину
опуклий
точка
перегину
угнутий
4) |
Оскільки
в інтервалах
Оскільки під час переходу через точки , друга похідна досліджуваної функції змінює знак, то це точки перегину. |
5) |
Значення
функції в точках перегину:
|
Приклад 8.6. |
Знайти
точки перегину, інтервали опуклості
і угнутості графіка функції
|
Розв’язання.
1) |
Знайдемо другу похідну:
|
2) |
Знайдемо
критичні
точки другого роду функції
,
в яких друга похідна дорівнює нулю 0
або
не існує.
|
3) |
Визначимо знак другої похідної зліва і праворуч від кожної критичної точки, представимо в результати в таблиці 8.5: |
Таблиця 8.5
Результати дослідження знаку другої похідної
-

0
‑
0
+
0
+
графік
опуклий
точка
перегину
угнутий
угнутий
4) |
Оскільки
в інтервалах
Оскільки під час переходу через точку друга похідна досліджуваної функції змінює знак, то це точка перегину.
Оскільки
під час переходу через точку
|
5) |
Знайдемо
значення функції в точці перегину:
Отже,
|
