
- •8. Дослідження функції однієї змінної
- •8.1. Умови монотонності та екстремуму
- •Послідовність дій при дослідженні функції на монотонність
- •Послідовність дій при дослідженні функції на екстремум за допомогою першої похідної
- •Послідовність дій при дослідженні функції на екстремум за допомогою другої похідної
- •8.2. Умови опуклості, угнутості, перегину функції
- •Послідовність дій при дослідженні функції на опуклість, угнутість і точки перегину
- •8.3. Схема повного дослідження функції однієї змінної
- •9. Застосування похідної для знаходження границь та екстремальних значень функцій однієї та багатьох змінних
- •9.1. Правило Лопіталя
- •9.2. Знаходження найбільших (найменших) значень функції однієї змінної
- •Послідовність дій при знаходженні найбільшого і найменшого значень функції на відрізку
- •9.3. Екстремум функції двох змінних
- •Контрольні питання зі змістового модуля IV
- •Змістовий модуль II Границі функції
- •Змістовий модуль III Диференціальне числення функцій однієї та багатьох змінних
- •Змістовий модуль IV Застосування похідної
- •Література
- •Предметний покажчик
- •МатематИка для економістів: вища математика
- •83023, М. Донецьк, вул. Щорса, 31.
- •83023, М. Донецьк, вул. Харитонова, 10.
ЗМІСТОВИЙ МОДУЛЬ 4
Застосування похідної
8. Дослідження функції однієї змінної
8.1. Умови монотонності та екстремуму
|
Функцію
називають
зростаючою (неспадаючою) в
деякому інтервалі Х,
якщо для будь-яких
Функцію
називають спадаючою
(незростаючою) в
деякому інтервалі Х,
якщо для будь-яких
,
виконується нерівність
|
|
Визначену на деякому інтервалі зростаючу (спадаючу), або незростаючу (неспадаючу) функцію називають монотонною функцією. |
Теорема 8.1. |
(критерій монотонності функції)
Нехай
функція
|
Теорема 8.2. |
(критерій зростання (спадання) функції) Якщо функція визначена, неперервна та має скінченну похідну в усіх точках деякого інтервалу. Тоді для того, щоб була зростаючою (спадаючою) на цьому інтервалі, необхідно та достатньо виконання умов: 1) в усіх точках інтервалу; 2) не стає тотожньо нулем ні у якому проміжку з цього інтервалу.
|
Теорема 8.3. |
(достатня умова зростання (спадання) функції)
Якщо
в усіх точках деякого інтервалу перша
похідна функції
додатна
|
Теорема 8.4. |
(необхідна умова зростання (спадання) функції)
Якщо
диференційована функція
зростає на деякому інтервалі, то
похідна її невід’ємна
|
Геометрично умова означає, що дотична до графіка монотонно зростаючої функції утворює з додатнім напрямом осі Ох гострий кут або паралельна їй.
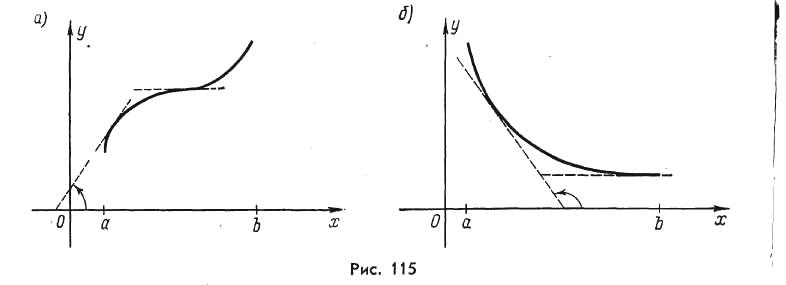
Рисунок 10.1 – Графік монотонно зростаючої функції
Дотична до графіка монотонно спадаючої функції утворює з додатнім напрямом осі Ох тупий кут або паралельна їй.
Рисунок 10.2 – Графік монотонно спадаючої функції
|
Точки,
в
яких функція
|
Зауваження. |
При дослідженні функції на монотонність, слід перш за все знайти область визначення функції. |
