Лекція 3. Елементи векторної алгебри

Векторними називаються величини, визначені їх числовим значенням та напрямом.

Вектор – відрізок, який має визначену довжину та напрям і позначається або . Точка А - початок вектора, точка В - кінець. Довжина вектора називається його модулем або абсолютною величиною і позначається , напрямок АВ визначається променем АВ.

Два вектора та вважаються рівними, якщо рівні їх модулі та співпадають їх напрямки. Вектор не змінюється, якщо його перенести паралельно самому собі в будь-яку точку простору. Такий вектор називається ковзним.

Проекцією вектора на вісь ОХ називається довжина відрізку А₁В₁ цієї осі між проекціями А₁ та В₁ точок А та В, узята зі знаком “+”, якщо напрямок відрізку А₁В₁ співпадає з напрямком осі ОХ., та зі знаком “-“ , якщо напрямок відрізку А₁В₁ протилежний напрямку осі ОХ . Проекція дорівнює добутку модуля вектора на косинус кута між віссю та вектором:

(1.8)

одиничні вектори координатних осей називаються ортами.

Координати вектора це проекції вектора на осі координат

.

вектор можна записати через координати так:

.

Якщо вектор заданий точками та то його можна записати так:

.

Кути вектора з осями координат називаються напрямними, а напрямні косинуси визначаються як:

. (1.9)

і відповідають умові: .

модуль вектора дорівнює кореню квадратному із суми квадратів його координат:

. (1.10)

Приклад 1.13. Знайти вектор, який має одиничний модуль і такий напрямок, що і вектор .

Розв’язання.

Одиничний вектор знайдемо за формулою:

, (1.11)

де - довжина вектора .

;

.

Приклад 1.14. Знайти напрямні косинуси вектора .

Розв’язання.

Одиничний вектор має модуль, що дорівнює одиниці. Тому з формул (1.9) та (1.10) слідує, що

;

Відповіді, отримані в прикладах 1.13 і 1.14, повинні співпадати.

Колінеарні вектори – належать паралельним або одній і тій же прямій, а їх координати відповідають умовам:

. (1.12)

Компланарні вектори – належать паралельним або одній і тій же площині.

Протилежні вектори – два колінеарні вектори однакові за модулем та протилежно спрямовані.

3.1. Лінійні операції з векторами

Сумою векторів називається вектор , який замикає ламану, побудовану з даних векторів і проведений від початку вектора в кінець вектора , за умови, що початок вектора прикладений до кінця вектора , а початок вектора прикладений до кінця вектора .

Якщо вектори задані своїми проекціями , , то їх алгебраїчна сума дорівнює алгебраїчній сумі відповідних координат:

. (1.13)

добутком вектора на число k називається новий вектор, проекції якого є добуток числа k на відповідну координату:

,

модуль якого , а напрямок якого співпадає з , якщо k>0 або протилежний, якщо k<0.

Скалярний добуток векторів

Скалярним добутком двох векторів називається число, що дорівнює добутку модулів цих векторів та косинуса кута між ними:

. (1.14)

Скалярний добуток двох векторів це також добуток модуля одного з векторів на проекцію другого вектора на перший вектор:

. (1.15)

Властивості скалярного добутку:

1. .

2. .

3. Якщо , тоді . Отже :

. (1.16)

Якщо вектори задані координатами то

. (1.17)

Приклад 1.15. Знайти скалярний добуток вектора , та вектора, що виходить від точки B(1;0;1) до точки C(-2;1;0).

Розв’язання:

Скалярний добуток векторів обчислюється за формулою (1.17)

де .

Підставивши й у зазначену формулу, одержимо

.

Кут між векторами:

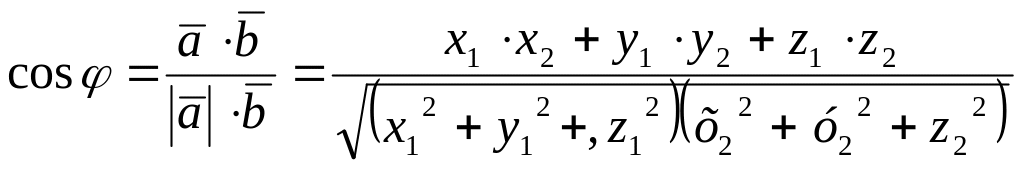. (1.18)

Умови перпендикулярності векторів:

. (1.19)

Приклад 1.16. Визначити координати вектора , колінеарного вектору , знаючи, що і він спрямований у тому ж напрямку, що і вектор .

Розв’язання.

Якщо вектори , тоді виконується співвідношення (1.12). Підставивши координати вектора , одержимо

або

, , .

Тоді

;

;

.

Так як вектори і спрямовані в одну сторону, тоді .

Отже,

.

Приклад 1.17. Знайти , якщо , .

Розв’язання:

Для розв’язування цієї задачі варто скористатися формулою:

.

Знайдемо і , пам'ятаючи, що , , .

,

.

Тоді

.

Приклад 1.18. Задано вектори: (0,1; 0,5; 2,7), =(1,4; 8,4; 9,1), =(5,6; 2,8; 5,1), = (8,5; 8,2; 9,3).

Знайти: вектори

1. = 6,2 ;

2. ;

3. довжину вектора ;

4. скалярний добуток векторів ;

5. кут між векторами та ;

6. знайти проекцію вектора на вектор .

Розв’язання.

1. Вектор =6,2 =(0,62; 3,1; 16,74).

2. Вектор =(1,4-5,6; 8,4-2,8; 9,1-5,1)=(-4,2; 5,6; 4,0).

3. Довжина вектора = .

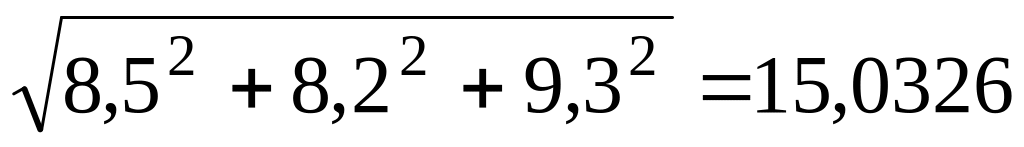4. Скалярний добуток векторів

;

5. Кут між векторами та :

.

6. Проекція вектора на вектор :

.