3. Обернена матриця

Якщо добуток двох квадратних матриць дорівнює одиничній матриці, тобто АС=Е, то матриця С називається оберненою по відношенню до А та позначається С=А^—1. матриця А є оберненою до матриці С, тобто А=С^-1. Тоді АА^-1=А^-1А=Е. Обернена матриця є переставною.

Властивості оберненої матриці:

– де

,

.

Для знаходження оберненої матриці треба виконати такі дії.

1. Обчислити визначник матриці А. Якщо 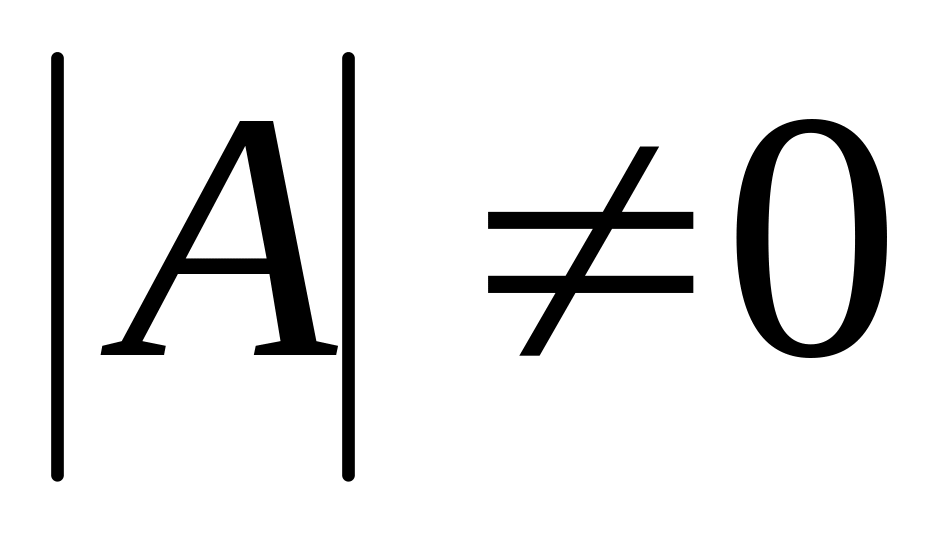, то матриця називається невиродженою, і в цьому випадку існує обернена матриця.

2. Обчислюються алгебраїчні доповнення кожного елемента а_ij матриці А і записуються у вигляді матриці С.

3. Транспонується матриця алгебраїчних доповнень С.

4. Обчислюється обернена матриця за формулою:

(1.4)

5. Виконується перевірка

Приклад 1.8.

Знайти обернену матрицю для

.

Розв’язання.

1. Обчислюємо визначник матриці А, розкладаючи його по першому рядку.

.

, тому обернена матриця існує.

2. Обчислюємо алгебраїчні доповнення всіх елементів.

,

,

.

Запишемо матрицю алгебраїчних доповнень

.

3. Транспонуємо матрицю С.

.

4. Обернена матриця

.

5. Перевірка.

Приклад 1.9. Знайти обернену матрицю для матриці

Розв’язання.

1. Обчислюємо визначник матриці А, дописавши два стовпця

, тому обернена матриця існує.

2. Обчислюємо алгебраїчні доповнення всіх елементів.

,

,

.

3. С- матриця алгебраїчних доповнень.

.

4. Транспонуємо матрицю С.

.

5. Обернена матриця.

.

5. Перевірка

Лекція 2. системи лінійних рівнянь

Знаходження розв’язку системи лінійних рівнянь можна проводити за допомогою формул Крамера, методом оберненої матриці, або методом Гаусса.

2.1. Формули Крамера

Для розв’язання системи лінійних рівнянь за формулами Крамера визначник квадратної матриці коефіцієнтів не повинен дорівнювати нулю. В цьому випадку система лінійних рівнянь буде мати лише один розв’язок, який знаходиться за формулами:

, (1.5)

де - визначник матриці коефіцієнтів системи лінійних рівнянь,

- визначник відповідної змінної, який отриманий заміною відповідного стовпця коефіцієнтів стовпцем вільних членів системи лінійних рівнянь.

Приклад 1.10. Розв’язати систему лінійних рівнянь методом Крамера:

Розв’язання. Складемо і обчислимо визначники:

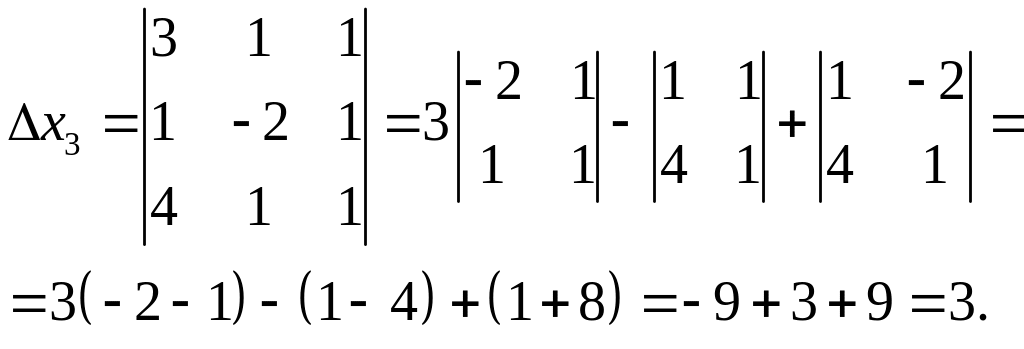
Підставимо одержані результати у формули (1.5). Маємо

Відповідь: .

2.2. Метод оберненої матриці

Матричний спосіб можна застосувати також тільки у випадку, якщо кількість рівнянь і кількість невідомих співпадають, а крім того, матриця системи має обернену.

Запишемо систему трьох рівнянь з трьома невідомими у матричному вигляді. Для цього введемо матриці виду:

.

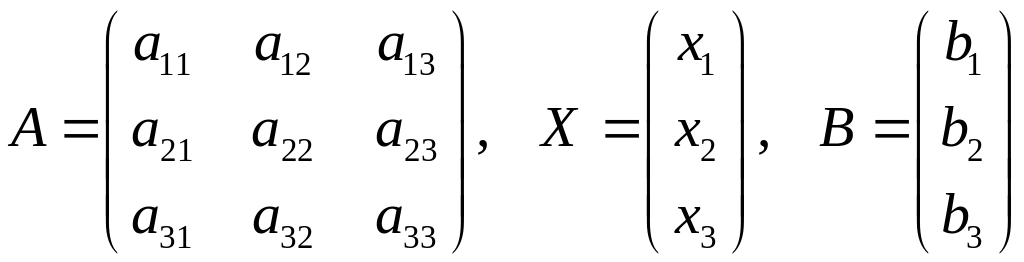Користуючись правилом множення матриць, систему (5) запишемо у матричному вигляді

. (1.6)

Помножимо рівняння (1.6) на обернену матрицю , отримаємо:

.

Розв’язок цього рівняння має вигляд

, (1.7)

де є оберненою матрицею до матриці .

Приклад 1.11. Розв’язати систему лінійних рівнянь попереднього прикладу матричним способом.

Розв’язання. Перепишемо задану систему у вигляді (1.6). Для цього складемо матриці виду

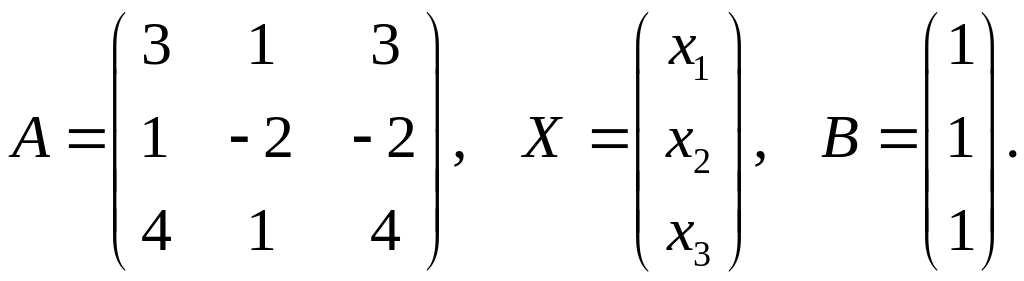
Розв’язок системи будемо шукати у вигляді (1.7). Необхідно знайти обернену матрицю до матриці . Обернена матриця існує, бо (див. приклад 1.10). Знайдемо алгебраїчні доповнення для кожного елемента матриці :

Складемо обернену матрицю згідно формули (1.4). Одержимо

.

Помножимо обернену матрицю на матрицю і одержимо шукану матрицю . Маємо

.

Відповідь: .

2.3. Метод Гаусса.

Для розв’язування систем лінійних рівнянь застосовують метод, який називають методом Гаусса або методом виключення змінних. Розв’язування систем лінійних рівнянь розглянемо за допомогою матриць. Його ідея полягає у зведенні розширеної матриці системи за допомогою елементарних перетворень матриці до трикутної матриці.

Трикутною називають матрицю, у якої під головною діагоналлю всі елементи дорівнюють нулю.

Елементарними перетвореннями матриці є такі перетворення:

1. перестановка двох рядків матриці;

2. множення всіх елементів рядка на одне і те ж число, відмінне від нуля;

3. додавання елементів якого-небудь рядка матриці, помножених на одне і те ж число, до відповідних елементів іншого рядка;

4. відкидання рядків матриці, елементами яких є нулі.

Проводячи елементарні перетворення над матрицею системи, отримують нову систему рівнянь, яка еквівалентна заданій, але з новими коефіцієнтами та вільними членами. Одержують трикутну систему рівнянь, із якої визначають невідомі.

Приклад 1.12. Методом Гаусса розв’язати систему лінійних рівнянь

Розв’язання. Складемо розширену матрицю системи і будемо робити над нею необхідні елементарні перетворення, щоб одержати трикутну матрицю. На початку переставимо перше і третє рівняння місцями, а потім помножимо елементи першого рядка відповідно на мінус три, мінус два та мінус два і одержані результати додамо відповідно до елементів другого, третього та четвертого рядків. Аналогічно вчинимо з елементами другого, а потім третього рядків. Одержимо матрицю

  

    .

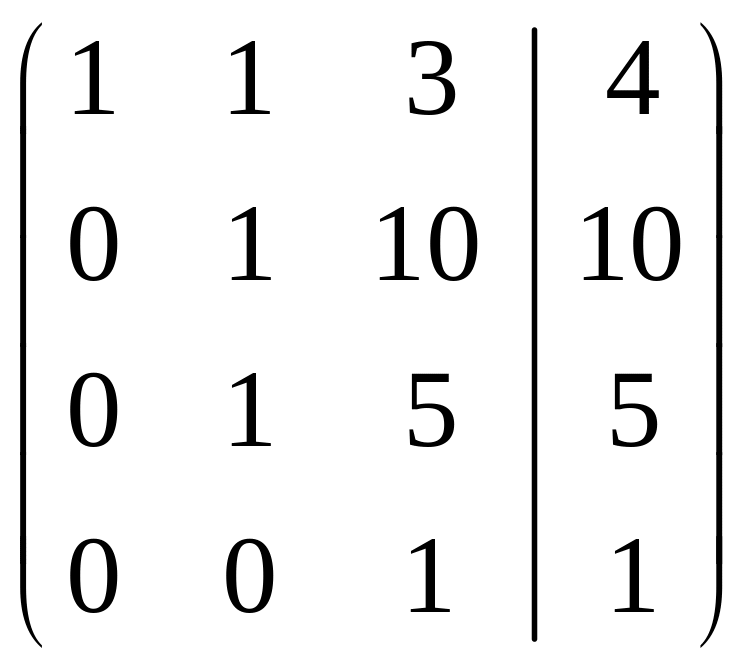
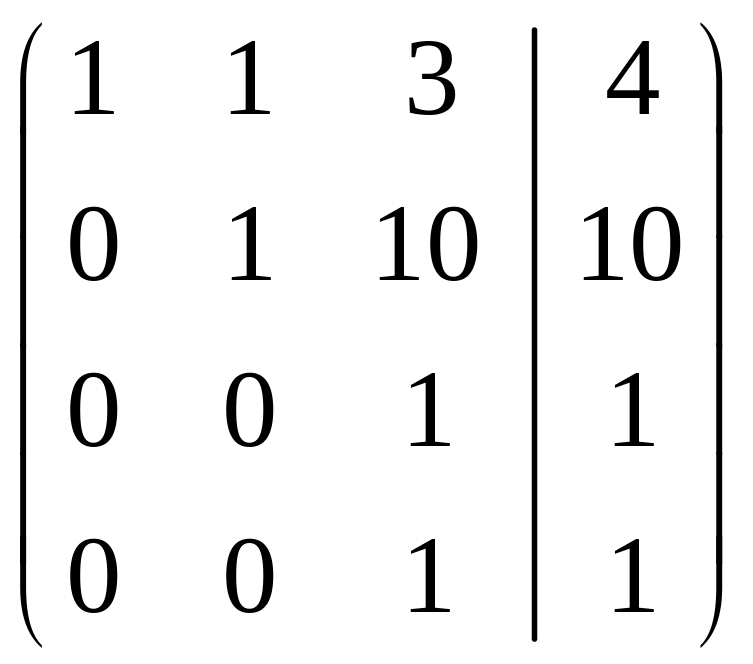
Система лінійних рівнянь матиме вигляд

З третього рівняння . З другого рівняння одержали , а з першого одержуємо .

Відповідь: .