7.4. Загальна схема дослідження функції. Побудова графіків функцій

Схема дослідження функції.

1. Знайти область визначення функції.

2. Знайти точки розриву (якщо вони є) та визначити їх вид.

3. Визначити асимптоти графіка функції.

4. Визначити парність, непарність і тим самим симетричність графіка функції.

5. Знайти точки екстремуму, інтервали монотонності.

6. Знайти точки перегину, інтервали опуклості й угнутості графіка функції.

7. За отриманими даними побудувати графік функції. Для уточнення графіка функції іноді корисно визначити точки перетину графіка з осями координат.

Приклад 2.54. Провести повне дослідження функції та побудувати її графік.

Розв’язання.

1) Знайдемо область визначення функції: .

2) Функція неперервна на всій осі як елементарна.

3) У графіка цієї функції відсутні асимптоти. Якщо функція неперервна, то відсутні вертикальні асимптоти. При знаходженні похилих асимптот параметр не дорівнює скінченному числу:

.

4) Функція не є ні парною, ні непарною:

5) Знайдемо інтервали монотонності та критичні точки функції за допомогою першої похідної.

.

О держані точки розбивають область визначення функції на такі інтервали: . Знайдемо знак похідної в кожному з інтервалів.

6) Знайдемо інтервали угнутості та точки перегину графіка функції за допомогою похідної другого порядку.

.

Критичні точки другого порядку розбивають область визначення функції на інтервали вгнутості. Знайдемо знак другої похідної у кожному з них.

.

Точки перегину функції мають координати: і .

7) Знайдемо точки перетину функції з осями координат: при ; при . Для рівняння можна методом підбору знайти один корінь .

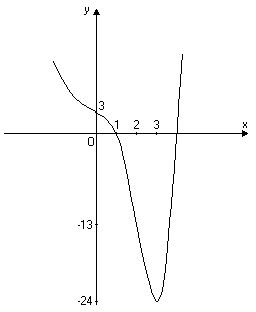
Побудуємо схематично графік функції (рис. 2.12).

Рис. 2.12

Приклад 2.54. Провести повне дослідження функції та побудувати її графік.

Розв’язання. 1) Знайдемо область визначення функції. Необхідно знайти ті точки, в яких знаменник дробу дорівнює нулю і виключити їх. Одержимо . Функція визначена в інтервалах .

2) Точки розриву другого роду:

3) Знайдемо асимптоти графіка функції.

а) Вертикальні асимптоти будемо шукати в точках розриву функції. Одержимо:

прямі та є вертикальними асимптотами функції.

б) Похилі асимптоти будемо шукати у вигляді , а невідомі параметри і визначимо за формулами (2.23). Одержимо

, тоді – вісь – горизонтальна асимптота.

4) Для функції виконується умова

.

Функція непарна, а її графік центрально-симетричний відносно початку координат.

5) Знайдемо інтервали монотонності та критичні точки функції. Для цього знайдемо першу похідну функції. Маємо:

;

.

Тоді для всіх із області неперервності.

Т обто функція спадна на кожному інтервалі області визначення.

6) Знайдемо інтервали вгнутості та точки перегину графіка функції. Для цього знайдемо другу похідну.

Прирівняємо . Одержимо ; – критична точка.

Знайдемо знак другої похідної в кожному з інтервалів .

Маємо .

На інтервалах та графік опуклий, а на інтервалах та – вгнутий. Точка є точкою перегину графіка функції.

7) Знайдемо точки перетину графіка функції з осями координат: при , при . Інших точок не існує.

Використовуючи результати досліджень, побудуємо графік функції (рис. 2.13).

Рис. 8

Рис. 8

Рис. 2.13

Побудуємо графік функції. Графік перетинає осі координат у точці О(0;0).