Типи точок розриву

Точки розриву бувають першого і другого роду.

Точка розриву х0 функції f(x) називається точкою розриву першого роду, якщо існують скінченні односторонні границі функції f(x) праворуч і ліворуч при x  х0, не рівні між собою, тобто .

Точка розриву х0 функції f(x) називається усувною, якщо границя функції існує, тобто . f(x) при x  х0, але не дорівнює значенню функції в цій точці, .

Точка розриву х0 функції f(x) називається точкою розриву другого роду, якщо хоча б одна з односторонніх границь функції f(x) праворуч або ліворуч при x  х0, дорівнює нескінченності або не існує.

Так у розглянутих вище прикладах маємо наступні точки розриву.

У прикладі 2.29 у точці х = 1 маємо розрив другого роду. У прикладі 2.30 у точці х = 0 маємо розрив першого роду. У прикладі 2.31 у точці х = 0 маємо усувний розрив.

Приклад 2.33. Який розрив має функція ?

Розв’язання. У точці функція не існує. Лівостороння границя , а правостороння .

Оскільки кожна з односторонніх границь нескінченна, то х = 3 є точкою розриву другого роду.

Приклад 2.34. Дослідити неперервність у точці х = 0 функції f(x) =  .

Розв’язання. У точці х = 0 функція f(x) = не визначена, отже, вона розривна в цій точці. Для з'ясування типу точки розриву знайдемо односторонні границі: , .

Оскільки одна з односторонніх границь нескінченна, то х = 0 є точкою розриву другого роду.

Лекція 6. Похідна і диференціал

1. Задачі, що приводять до поняття похідної

Поняття похідної є одним з основних математичних понять. Похідна широко використовується при розв’язуванні цілої низки задач математики, фізики, економіки, інших наук. Необхідність у використанні похідної виникає тоді, коли ставиться задача, наприклад, визначити швидкість протікання процесів, побудувати функцію, що приблизно описує поведінку заданої, обчислити похибки вимірювань.

Швидкість прямолінійного руху

Нехай матеріальна точка (деяке тіло) М рухається нерівномірно по деякій прямій. Кожному значенню часу t відповідає певна відстань ОМ = S до деякої фіксованої точки О. Ця відстань залежить від часу t, що минув, тобто S = S(t).

Цю рівність називають законом руху точки. Необхідно знайти швидкість руху точки.

Якщо в деякий момент часу t точка займає положення М, то у момент часу t+∆t (∆t – приріст часу) точка займе положення M₁, де ОM₁ =S+∆S (∆S – приріст відстані). Таким чином, переміщення точки М за час ∆t буде ∆S = S(t + ∆t) – S(t).

Відношення виражає середню швидкість руху точки за час ∆t:

Середня швидкість залежить від значення ∆t: чим менше ∆t, тим точніше середня швидкість виражає швидкість руху точки в даний момент часу t.

Межа середньої швидкості руху при прагненні до нуля проміжку часу ∆t називається швидкістю руху точки в даний момент часу (або миттєвою швидкістю). Позначивши цю швидкість через V, отримаємо

або = (2.10)

Дотична до кривої

Дамо спочатку загальне визначення дотичної до кривої.

Візьмемо на неперервній кривій L дві точки М і М₁ (див. рис. 2.5).

Пряму M M₁, що проходить через ці точки, називають січною.

Нехай точка М₁, рухаючись уздовж кривої L, необмежено наближається до точки М. Тоді січна, повертаючись біля точки М, прямує до деякого граничного положення МТ.

Дотичною до даної кривої в даній точці М називається граничне положення МТ січної MM₁, що проходить через точку М, коли друга точка перетину M₁ необмежено наближається по кривій до точки M.

Рис. 2.5	Рис. 2.6

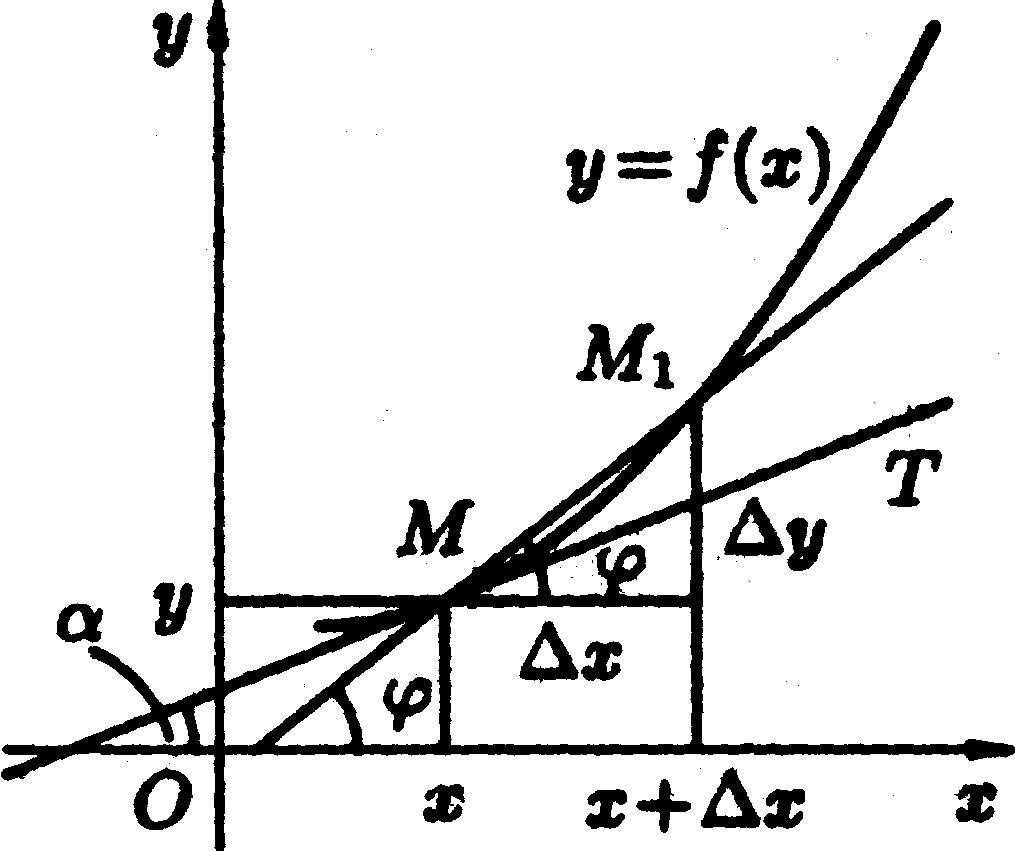
Розглянемо тепер графік неперервної кривої у = f(x), який має в точці М (х;у) невертикальну дотичну. Знайдемо її кутовий коефіцієнт, , де  – кут дотичної з віссю Ох.

Для цього проведемо через точку М і точку M₁ графіка з абсцисою х+∆х січну (див. рис. 2.6). Позначимо через  — кут між січною MM₁ і віссю Ох. На рисунку видно, що кутовий коефіцієнт січної дорівнює

При через неперервність функції приріст ∆y теж прямує до нуля; тому точка M₁ необмежено наближається по кривій до точки М, а січна MM₁, повертаючись біля точки М, переходить в дотичну. Кут, тобто . Звідси отримуємо геометричний зміст похідної

(2.11)

Економічний зміст похідної. Використання поняття похідної в економіці

Розглянемо задачу про продуктивність праці. Нехай функція и = и(t) відображає кількість виробленої продукції u за час t i необхідно знайти продуктивність праці в момент t₀.

За період часу від t₀ до t₀ + t кількість виробленої продукції зміниться від значення u₀ = u(t₀) до значення u₀ + u = u(t₀ + t); тоді середня продуктивність праці за цей період часу z_сер= . Очевидно, що продуктивність праці в момент t₀ можна визначити як граничне значення середньої продуктивності за період часу від t₀ до t₀ + t при t  0 , тобто

Таким чином, продуктивність праці є похідна від обсягу виробленої продукції по часу.

Розглянемо ще одне поняття, яке ілюструє економічний зміст похідної.

Витрати виробництва y будемо розглядати як функцію кількості продукції х, що виробляється. Нехай х — приріст продукції, тоді y — приріст витрат виробництва і – середній приріст витрат виробництва продукції на одиницю продукції. Похідна у' = виражає граничні витрати виробництва і характеризує наближено додаткові затрати на виробництво одиниці додаткової продукції.

Граничні витрати залежать від рівня виробництва (кількість продукції, що випускається) і визначаються не постійними виробничими затратами, а лише змінними (на сировину, паливо та ін.). Аналогічним чином можуть бути визначені гранична виручка, граничний доход, граничний продукт, гранична корисність, гранична продуктивність та інші граничні величини.

Застосування диференціального числення для дослідження економічних об'єктів та процесів на основі аналізу цих граничних величин дістало назву граничного аналізу. Граничні величини характеризують не стан (як сумарна чи середня величини), а процес зміни економічного об'єкта. Таким чином, похідна виступає як швидкість зміни деякого економічного об'єкта (процесу) за часом або відносно іншого об'єкта дослідження. Але необхідно врахувати, що економіка не завжди дозволяє використовувати граничні величини в силу неподільності багатьох об'єктів економічних розрахунків та перервності (дискретності) економічних показників в часі (наприклад, річних, квартальних, місячних та ін.). Водночас у деяких випадках можна відокремитись від дискретності показників і ефективно використовувати граничні величини.