Міністерство освіти і науки
Донецький національний університет економіки і торгівлі
імені Михайла Туган-Барановського
Кафедра вищої і прикладної математики
Фортуна В.В.
Прикладна математика Курс лекцій
для студентів денної форми навчання
напряму підготовки «Товарознавство і торгівельне підприємництво»
Затверджено:
Протокол засідання кафедри
вищої і прикладної математики
№ 18 від 14 січня 2013 р.
Д онецьк 2013
ЗМІСТ
стор.
Лекція 1 |
Моделі рядів динаміки . ...... ...... ...... ...... ...... ...... ...... ...... ...... ...………... |
3 |
Лекція 2 |
Автокореляція даних та залишків ... ... ...... ...... ...... ...... ...... ...... ...... .. |
7 |
|
Автокореляція даних |
|
|
Автокореляція залишків ... ... ...... ...... ...... ...... ...... ...... ...... .. |
|
Лекція 3 |
Мультиколінеарність…………………... .. ...... ...... ……………………… |
10 |
Лекція 4 |
Множинна регресія………………………………………… |
15 |
Лекція 5 |
Рангова кореляція………………………………… |
20 |
|
Випадок двох експертів, …………………… |
|
|
Випадок багатьох експертів……………………………… |
|
Лекція 6 |
Мережеве планування……………………………………… |
24 |
Лекція 1 моделі рядів динаміки
Однією з найважливіших задач дослідження економічних процесів є вивчення зміни економічних показників з часом (товарообігу, обсягу випуску продукції, продуктивності праці і т.д.). Ця задача вирішується за допомогою упорядкування й аналізу рядів динаміки.
Динамічним рядом називається послідовність результатів спостережень за явищем через рівні проміжки часу.
Вивчаючи ряди динаміки, прагнуть виявити основну, головну тенденцію в зміні показників ряду. Аналітичне моделювання рядів динаміки проводиться за допомогою найпростіших економіко-математичних моделей: лінійної, параболічної, гіперболічної, логарифмічної, показникової, степеневої та інших.
Приклад 1.
Проаналізувати показники реалізації борошняних виробів у державній торгівлі Донецької області за ряд років. Знайти рівняння лінійної, параболічної і гіперболічної залежностей. Перевірити адекватність отриманих економіко-математичних моделей, визначити найкращу модель.
Роки |
1991 |
1992 |
1993 |
1994 |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
Реалізація виробів, тис.т |
12,1 |
12,9 |
13,7 |
13,9 |
14,5 |
15,1 |
15,7 |
16,1 |
16,6 |
17,1 |
Розв’язок. Дані таблиці показують, що реалізація продукції неухильно зростала, хоча відбувалося це нерівномірно. Очевидно, існує ряд чинників, під впливом яких змінюється величина реалізації. Деякі з чинників можуть діяти довгостроково, а інші – короткочасно; деякі можуть бути істотними, інші – випадковими.
Для вирівнювання показника реалізації борошняних виробів у державній торгівлі використовуємо такі функції: лінійну, параболічну і гіперболічну. Параметри обраних для моделювання функцій можна знаходити за допомогою методу найменших квадратів. На його основі для кожній із функцій формують спеціальну систему рівнянь Гаусса. Для вказаних функцій приведемо відповідні системи:
Лінійна
-
|
(1) |
Параболічна
-
|
(2) |
Гіперболічна
-
|
(3) |
У
кожній із систем (1)-(3)
– результативний показник;
– чинник часу;
– кількість спостережень;
– параметри моделей.
Відлік часового показника починають із 1. Складемо допоміжну розрахункову таблицю 1 і на її основі сформуємо системи Гаусса.
Таблиця 1 - Допоміжні розрахунки для формування систем Гаусса
х |
у |
x2 |
x3 |
x4 |
уx |
yx2 |
1/x |
1/x2 |
y/x |
1 |
12,1 |
1 |
1 |
1 |
12,1 |
12,1 |
1 |
1 |
12,1 |
2 |
12,9 |
4 |
8 |
16 |
25,8 |
51,6 |
0,5 |
0,25 |
6,45 |
3 |
13,7 |
9 |
27 |
81 |
41,1 |
123,3 |
0,333 |
0,111 |
4,5667 |
4 |
13,9 |
16 |
64 |
256 |
55,6 |
222,4 |
0,25 |
0,0625 |
3,475 |
5 |
14,5 |
25 |
125 |
625 |
72,5 |
362,5 |
0,2 |
0,04 |
2,9 |
6 |
15,1 |
36 |
216 |
1296 |
90,6 |
543,6 |
0,167 |
0,0278 |
2,5167 |
7 |
15,7 |
49 |
343 |
2401 |
109,9 |
769,3 |
0,1428 |
0,0204 |
2,2429 |
8 |
16,1 |
64 |
512 |
4096 |
128,8 |
1030,4 |
0,125 |
0,0156 |
2,0125 |
9 |
16,6 |
81 |
729 |
6561 |
149,4 |
1344,6 |
0,111 |
0,0123 |
1,844 |
10 |
17,1 |
100 |
1000 |
10000 |
171 |
1710 |
0,1 |
0,01 |
1,71 |
55 |
147,7 |
385 |
3025 |
25333 |
856,8 |
6169,8 |
2,9288 |
1,5496 |
39,8178 |
У останньому рядку таблиці 1 вказані суми всіх значень для кожного стовпця.
Складемо системи для трьох функцій і знайдемо відповідні рівняння.
Для визначення параметрів рівняння лінійної функції запишемо систему рівнянь (1) і знайдемо її розв’язок:
Таким
чином,
– лінійна модель.
Для визначення параметрів рівняння параболічної функції запишемо систему рівнянь (2) і знайдемо її розв’язок за допомогою методу Гаусса:
Таким
чином,
– параболічна модель.
Для визначення параметрів рівняння гіперболічної функції запишемо систему рівнянь (3) і знайдемо її розв’язок
Таким
чином,
– гіперболічна модель.
Адекватність економіко-математичної моделі може бути встановлена за допомогою середньої помилки апроксимації (середнього відсотку розбіжності теоретичних і фактичних значень):
,
(4)
де
–
фактичні значення показника,
– теоретичні значення, знайдені за
рівнянням.
Для цього за кожним рівнянням знаходять теоретичні значення , підставляючи в них відповідні значення , і для кожного значення
розраховують
,
потім знаходять середнє значення
.
При
моделюванні економічних показників
частіше усього припускається 5% похибка
(іноді 7%, рідко 10%). Модель рахується
адекватною (тобто придатною), якщо
.
Вибір найкращої моделі можна проводити на основі залишкового середньоквадратичного відхилення (залишкової дисперсії):
,
(5)
де
–
кількість параметрів у рівнянні.
Кращою
буде та функція, для котрої значення
менше.
Таблиця 2 - Розрахунки для лінійної функції
-
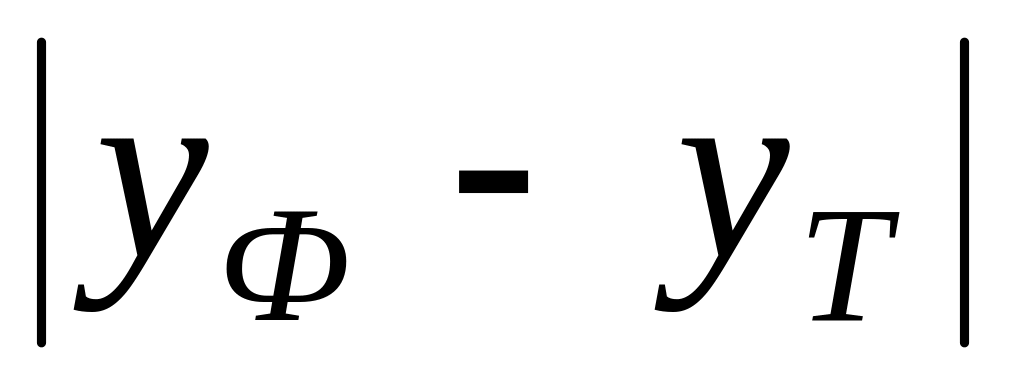
1
12,1
12,3458
0,2458
1,991
0,060418
2
12,9
12,8846
0,0154
0,1195
0,000237
3
13,7
13,4234
0,2766
2,0606
0,076508
4
13,9
13,9622
0,0622
0,4455
0,003869
5
14,5
14,501
0,001
0,0069
0,000006
6
15,1
15,0398
0,0602
0,4003
0,003624
7
15,7
15,5786
0,1214
0,7793
0,014738
8
16,1
16,1174
0,0174
0,1079
0,000303
9
16,6
16,6562
0,0562
0,3374
0,003158
10
17,1
17,195
0,095
0,5525
0,009025
6,8008
0,17188
З
формул (4), (5) маємо:
;
.
Таблиця 3 - Розрахунки для параболічної функції
-
1
12,1
12,2251
0,1251
1,023305
0,01565
2
12,9
12,8445
0,0555
0,432092
0,00308
3
13,7
13,4437
0,2563
1,906469
0,06569
4
13,9
14,0227
0,1227
0,87501
0,015055
5
14,5
14,5815
0,0815
0,558927
0,006642
6
15,1
15,1201
0,0201
0,132936
0,000404
7
15,7
15,6385
0,0615
0,39326
0,003782
8
16,1
16,1367
0,0367
0,227432
0,001347
9
16,6
16,6147
0,0147
0,088476
0,000216
10
17,1
17,0725
0,0275
0,161078
0,000756
5,798984
0,112623
З
формул (4), (5) маємо:
;
.
Таблиця 4 - Розрахунки для гіперболічної функції
-
1
12,1
11,251
0,8489
7,5450
0,7206
2
12,9
13,739
0,83905
6,1070
0,7040
3
13,7
14,568
0,868367
5,9606
0,7541
4
13,9
14,983
1,083025
7,2283
1,1729
5
14,5
15,232
0,73182
4,8045
0,5356
6
15,1
15,398
0,297683
1,9333
0,0886
7
15,7
15,517
0,183843
1,1848
0,0338
8
16,1
15,605
0,4945
3,1720
0,2450
9
16,6
15,674
0,9259
5,9070
0,8573
10
17,1
15,729
1,3706
8,71355
1,8785
52,556
6,9904
З
формул (4), (5) маємо:
.
Оскільки
,
то
ця модель адекватною не являється і
рахувати для неї
не треба.
Складемо зведену таблицю для статистичних оцінювальних характеристик:
Таблиця 5 - Статистичні оцінки для досліджуваних моделей
Вид функції |
|
|
Лінійна |
0,68 |
0,147 |
Парабола |
0,579 |
0,127 |
Гіпербола |
5,25 |
– |
З
порівняння середніх помилок апроксимації
видно, що для гіперболічної функції
вона виходить за 5% рівень, в лінійної
моделі і параболічної ця характеристика
не виходить за 5% рівень і приблизно
однакова. Якщо оцінювати перевагу, то
очевидно, що кращою є параболічна
функція, оскільки у неї залишкове
середньоквадратичне відхилення
найменше.