Поскольку

,

, (10.7)

,

то: прямоугольные декартовые координаты вектора равны скалярным произведениям этого вектора на соответствующие базисные векторы.

Кроме того,

(10.8)

.

Следовательно, прямоугольные декартовые координаты вектора равны его проекциям на координатные оси.

Косинусы углов, образованных вектором с координатными осями (базисными векторами ) называют направляющими косинусами вектора .

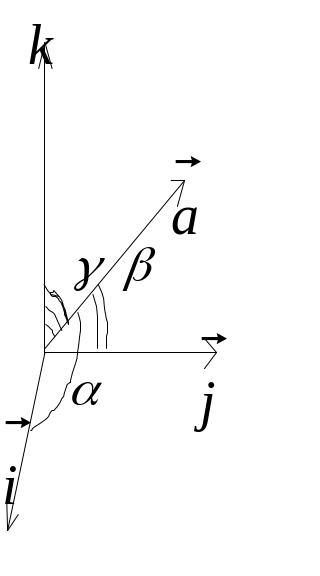
Из соотношений (10.8) следует, что

, (10.9)

и

(10.10)

Таким образом, сумма квадратов направляющих косинусов вектора равна 1.

В частности, если : , то

и, таким образом, вектор имеет координаты

. (10.11)

Для того чтобы найти расстояние между точками и пространства , достаточно применить формулу (10.4) к вектору :

(10.12)

§ 11. Векторное произведение двух векторов

Рассмотрим три некомпланарных вектора

Определение. Упорядоченная тройка векторов образует правую (левую) связку, если кратчайший поворот первого вектора до совмещения со вторым вектором в плоскости этих векторов происходит против движения (по движению) часовой стрелки, если смотреть с конца третьего вектора .

Рис. 11.1. Правая связка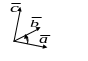

Определение. Векторным произведением вектора на вектор называют вектор , удовлетворяющий условиям:

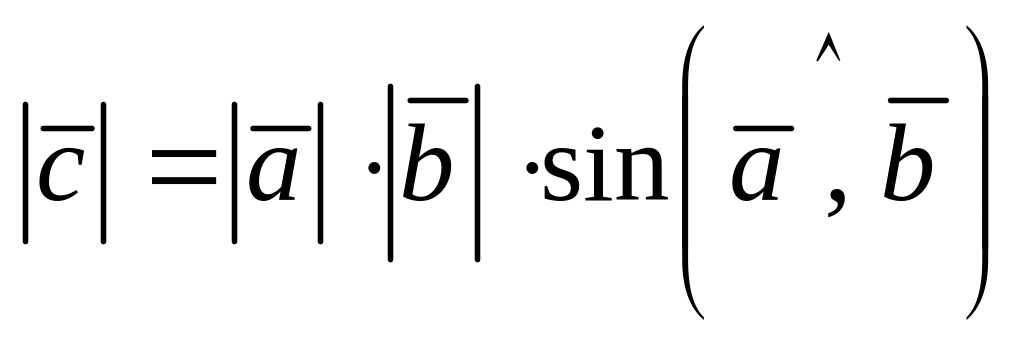1. ; (11.1)

2. ;

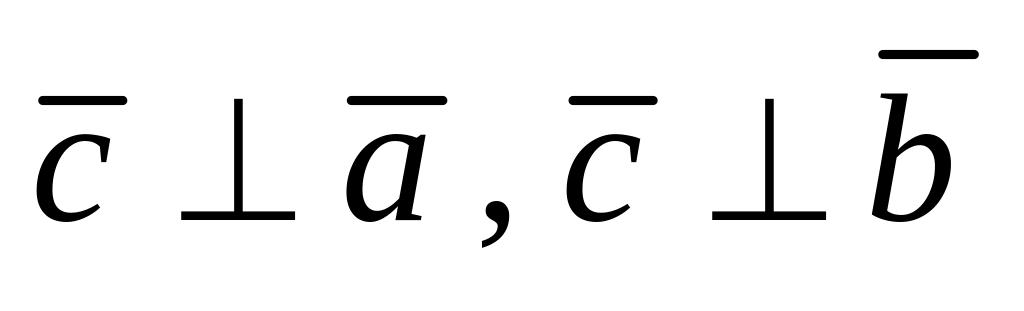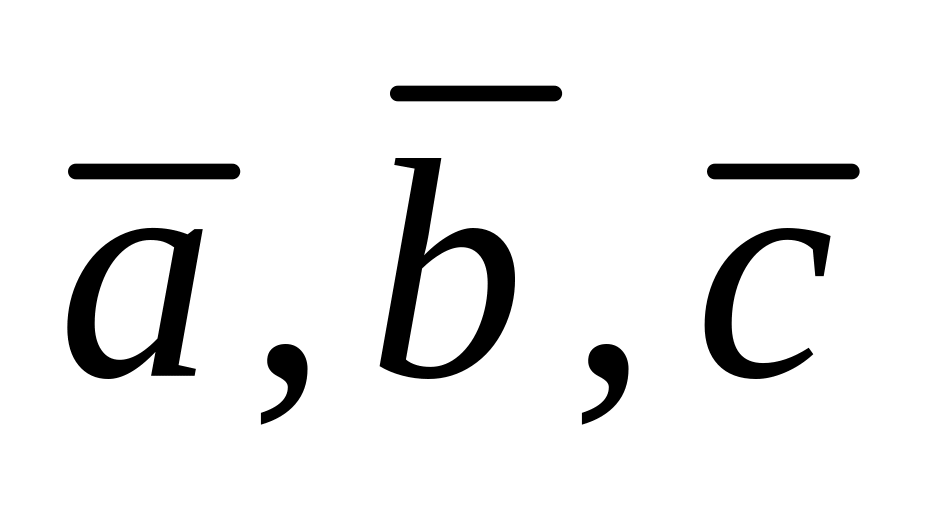3. – правая связка.

Замечания. 1. Условие 1) определения задает длину вектора, а условия 2) и 3) – направление.

2. Из условия 1) определения векторного произведения двух векторов следует, что модуль векторного произведения двух векторов численно равен площади параллелограмма, построенного на векторах-сомножителях.

Рис. 11.2.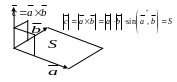

Теорема 11.1. Векторное произведение двух векторов равно нулю тогда и только тогда, когда векторы коллинеарны.

Доказательство: Необходимость. Пусть

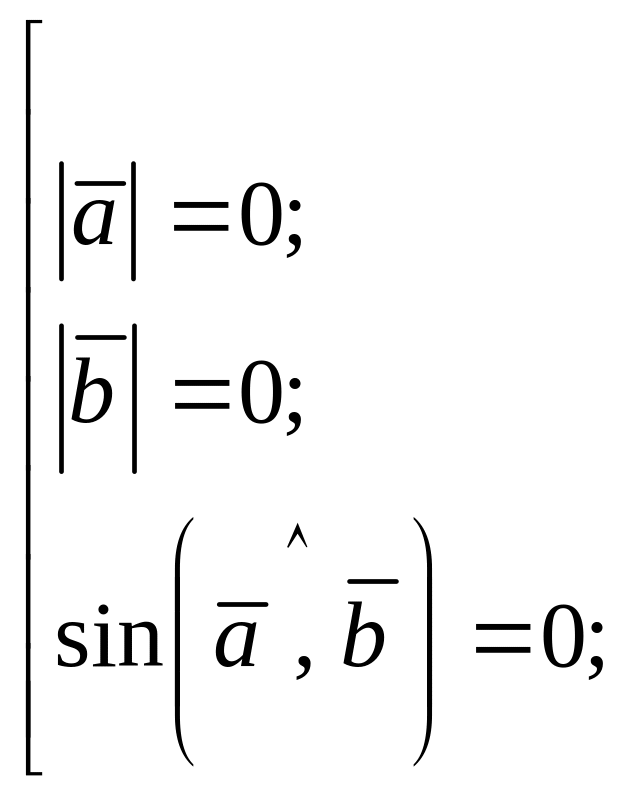
А так как имеет произвольное направление, то

Достаточность. Пусть

ч.т.д.

Следствие. . (11.2)

Свойства векторного умножения двух векторов:

1. ;

2. ;

3. , .

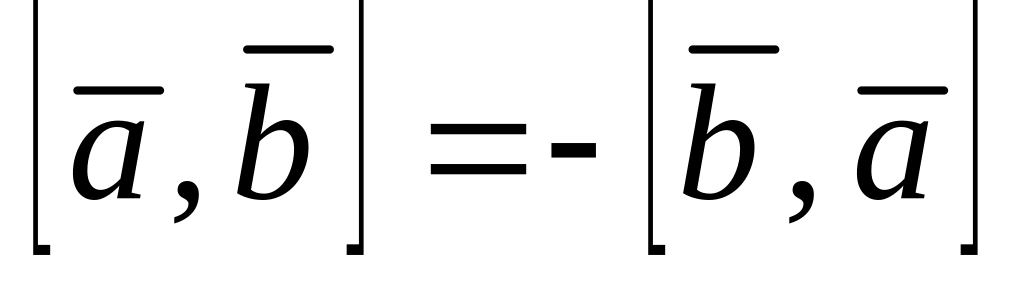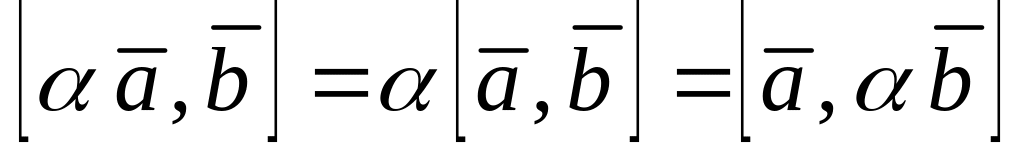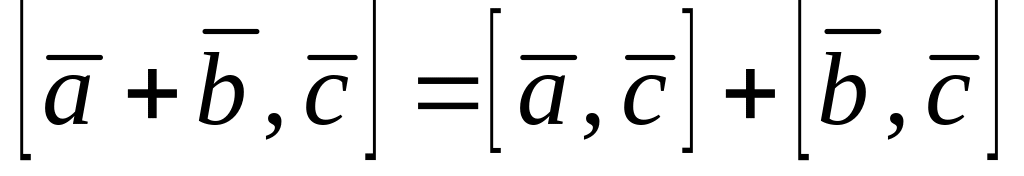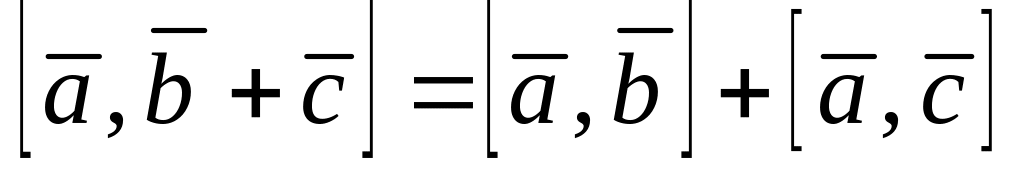Из указанных свойств следует, что векторное произведение одной линейной комбинации векторов на другую линейную комбинацию производится аналогично умножению одного многочлена на другой с учетом свойства антикоммутативности векторного умножения.

Пример. Найти площадь параллелограмма, построенного на векторах и , если

Решение. Используя определение векторного произведения двух векторов, получаем:

Ответ: .

Рассмотрим связь между векторным и скалярным произведениями двух векторов и .

Поскольку имеют место соотношения

и .

Поэтому нетрудно показать, что

.

А так как , , а значит и , то

. (11.3)

Равенство (11.3) называют основным соотношением векторной алгебры.

§ 12. Векторное произведение двух векторов в аффинных координатах

Пусть в в репере векторы и заданы разложениями: и .

Тогда

.

Так как

и

, , , то

. (12.1)

И окончательно получаем:

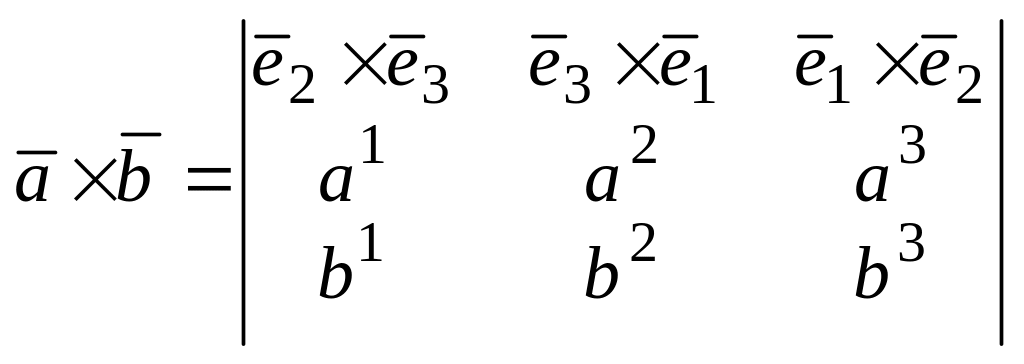(12.2)

Таким образом, векторное произведение двух векторов в аффинных координатах выражается формулой (11.2)