§7. Проекции вектора на ось

Определение. Проекцией точки на ось в направлении проектирующей плоскости (проектирующей прямой ) называют точку пересечения оси с плоскостью (с прямой ), проходящей через точку параллельно плоскости (прямой ).

Определение. Векторной проекцией вектора на ось называют вектор оси , для которого точка есть проекция точки , точка есть проекция точки на эту же ось:

. (7.1)

Определение. Скалярной проекцией вектора на ось называют число , абсолютная величина которого равна модулю векторной проекции вектора на ось , причем , если направление вектора совпадает с направлением оси , и в противном случае.

(7.2)

Нетрудно показать, что векторная и скалярная проекции вектора на ось связаны соотношением

. (7.3)

Теорема 7.1. Проекция суммы двух векторов на какую-либо ось равна сумме проекций векторов-слагаемых на эту же ось.

Замечание. Утверждение теоремы справедливо как для векторных проекций, так и для скалярных:

, (7.4)

. (7.5)

Теорема 7.2. Проекция произведения вектора на число на какую-либо ось равна произведению этого числа на проекцию данного вектора на эту же ось:

, (7.6)

. (7.7)

Следствие. Проекция на какую-либо ось линейной комбинации векторов равна точно такой же линейной комбинации (с теми же самыми коэффициентами) проекций на эту же ось векторов линейной комбинации.

Рассмотрим два произвольных (ненулевых) вектора и и отложим их от некоторой точки пространства.

Т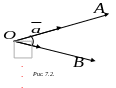 очка и вектор определяют луч , точка и вектор определяют луч . Лучи и в свою очередь определяют два угла. Тот из них, который не больше развернутого, будем называть углом между векторами и и обозначать .

Очевидно, что угол между векторами не зависит от выбора точки .

Определение. Углом между вектором и осью называют угол между вектором и ортом оси .

Теорема 7.3. Скалярная ортогональная проекция вектора на ось равна произведению модуля этого вектора на косинус угла между вектором и осью :

. (7.8)

Следствие. Равные векторы имеют равные проекции на одну и ту же ось

§8. Скалярное произведение двух векторов

Определение. Скалярным произведением двух векторов и называют число, равное произведению длин этих векторов на косинус угла между ними:

= . (8.1)

Теорема 8.1. Скалярное произведение двух векторов и равно нулю векторы и перпендикулярны.

Доказательство.

Необходимость. Пусть , т.е. . Это значит, что: 1) либо 2) либо 3) либо т.е. 1)

2) 3) . А т.к. направление нуль-вектора не определено, то можно считать, что он перпендикулярен любому вектору. Следовательно, в любом из 3-х случаев .

Достаточность. Пусть и

Теорема доказана.

Свойства скалярного произведения:

V₁. коммутативность

V₂. дистрибутивность

V₃. однородность

V₄. . неотрицательность

▲ (8.2)

Доказательство: 1) .

2) .

3) .

4) . ▲

• Определение. Скалярное произведение вектора на себя называют скалярным квадратом вектора.

• Скалярный квадрат вектора равен квадрату его модуля.

Следствие. Модуль вектора равен арифметическому квадратному корню из скалярного квадрата этого вектора

. (8.3)

Из свойств и определения скалярного произведения двух векторов следует, что

(8.4)

• На основании указанных свойств скалярное умножение двух линейных комбинаций векторов производится аналогично умножению одного многочлена на другой.

Например:

.

• Определение. n–мерное векторное пространство, удовлетворяющее аксиомам скалярного умножения V₁-V₄, называют евклидовым векторным пространством и обозначают .

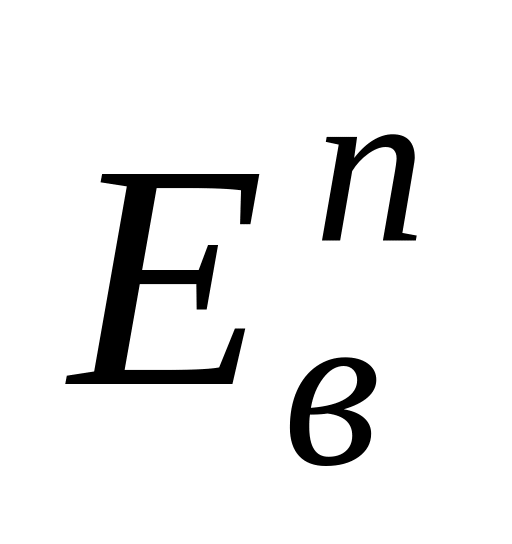• Определение. Аффинное пространство Аⁿ, удовлетворяющее аксиомам V₁-V₄, называют евклидовым точечно-векторным пространством и обозначают .

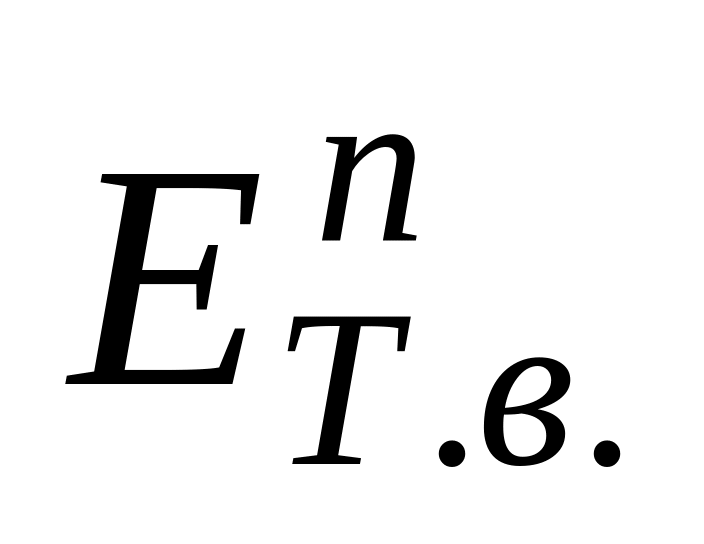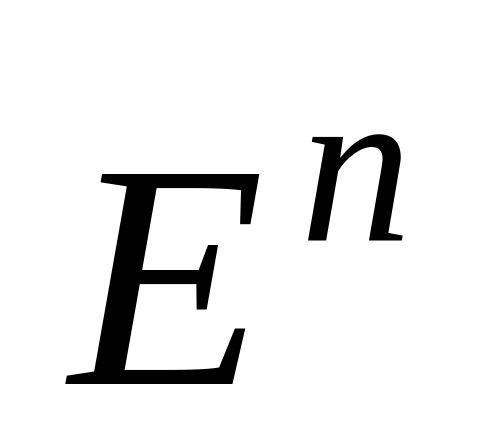• В литературе пространства обозначают через . В таких случаях из контекста определяют, какое именно пространство имеют в виду.

Определение. Геометрию, которая изучает свойства евклидовых пространств, называют евклидовой.