34

Заказ #671.

Обозначения: x^7 – икс в седьмой степени

С_7 – С с нижним индексом 7

00

1.Укажите классическую формулу нахождения вероятности и условия ее применимости.

1а. - применима, если количество благоприятных вариантов m(А) и общее количество вариантов исходов n – конечные натуральные числа, а также если все исходы равновероятны.

2.Дайте определение сочетаний и их числа . Сочетанием из   по   называется набор   элементов, выбранных из данного множества, содержащего   различных элементов. Число сочетаний из   по   равно биномиальному коэффициенту

3.Вычислите .

А³_{5 =} 5!/(5-3)! = 120/2 = 60, А^3_8 = 8!/5! = 6*7*8 = 336, C^5_8 = 8!/(5!*3!) = 7*8 = 56, C^7_9 = 9!/(7!*2!) = 4*9 = 36, P_4 = 4! = 1*2*3*4 = 24, P_6 = 6! = 720.

4.Что больше или

С^5_9 = 9!/(5!*4!) = 6*7*8*9/24 = 2*7*9 = 126

A^4_6 = 6!/2! = 3*4*5*6 = 12*30 = 360

C^5_9 < A^4_6

5.В конверте лежат 8 мужских фотогрфий и 4 женских. Берут сразу 3 фотографии. Найти вероятности того, что :? а)они все М.,б) они все Ж.

a) P(3 мужских фотографий) = C^3_8/С^3_12

б) Р(3 женские фотографии) = С^3_4/C^3_12

01

1.Укажите формулы математического ожидания и дисперсии д.с.в.

1а.

2.Дайте определение равновозможных событий и приведите пример таких событий

Равновозможные события – события, вероятность наступления которых одинакова. Пример: выпадение 1,2,3,4,5,6 на игральном кубике – равновероятные события.

3.Бросают сразу два игральных кубика. Какова вероятность выпадения неодинакового числа очков?

Всего вариантов: 6*6 = 36. Вариантов с одинаковыми цифрами на 2 кубиках = 6. Значит, подходящих вариантов 36-6 = 30. Поэтому вероятность: 30/36 = 5/6.

4.Бросают игральный кубик. Найдите условную вероятность выпадения четной цифры при условии, что выпала цифра, большая 3.

Может выпасть 4,5,6. Должна выпасть 2 или 3. Значит, вероятность искомая равна 2/3.

5.Составьте ряд распределения с.в., распределенной по биномиальному закону с параметрами . Укажите ее математическое ожидание и дисперсию.

P(X=0) = C^0_4*2^4/3^4 = 16/81

P(X=1) = C^1_4*2^3/3^4 = 32/81

P(X=2) = C^2_4*2^2/3^4 = 24/81

P(X=3) = C^3_4*2^1/3^4 = 8/81

P(X=4) = C^4_4*2^0/3^4 = 1/81

MX = 4/3, DX = 8/9

02

1.Укажите определение условной вероятности события по отношению к событию .

1А. Это вероятность события , найденная при условии, что произошло событие .

2.Дайте определение полной группы событий, чему равна вероятность суммы событий такой группы.

Полная группа событий - система случайных событий такая, что в результате произведенного случайного эксперимента непременно произойдет одно из них. Сумма вероятностей всех событий в группе всегда равна 1.

3.В конверте лежат 5 мужских (м) и 3 женских фотографии (ж) одного размера. Берут наугад сразу две фотографии. Найти вероятности того, что это окажутся: а)одна м, другая –ж; б) обе м; в)обе ж.

А) Вероятность: (C^1_5*C^1_3)/C^2_8

Б) Вероятность: С^2_5/C^2_8

В) Вероятность: С^2_3/C^2_8

4.С.в. распределена биномиально с параметрами . Найти вероятности событий и выяснить, зависимы ли эти события.

P(A) = P(X=2) = C^2_4/16 = 3/8

P(B) = P(X>0) = 1-P(X=0) = 1-1/16 = 15/16

Это зависимые события.

5.В ящике лежат 3 новых и 4 игранных тенисных мяча. Для тренировки спортсмен взял наугад 2 мяча, поиграл ими и положил назад в ящик. Для игры он опять наугад взял один мяч. Какова вероятность, что этот мяч новый?

I игра:

А_1 = 2 новых мяча; А_2 = 1 новый, 1 игранный; А_3 = 2 игранных

P(A_1) = C^2_3/C^2_7 = 3/21 = 1/7

P(A_2) = (C^1_3*C^1_4)/C^2_7 = (3*4)/21 = 12/21

P(A_2) = C^2_4/C^2_7 = 6/21

II игра:

B_1 = взял новый мяч

По формуле полной вероятности: P(B_1) = 1/7*1/7 + 12/21*2/7 + 6/21*3/7 = (3+24+18)/147 = 45/147.

03

1.Укажите расширенную формулу сложения:

1г. .

2.Дайте определение случаев, чему равна вероятность одного случая.

Случай, Случа́йное собы́тие — подмножество множества исходов случайного эксперимента. Вероятность одного случая равна частоте наступления события при стремлении количества повторяющихся экспериментов к бесконечности.

3.Из колоды в 36 карт берут одну за другой две карты. Какова вероятность, что вторая карта – Туз?

A_1 = I карта туз

P(A_1) = 4/36 = 1/9

P(вторая карта туз) = 1/9*3/35 + 8/9*4/36 = 1/105 + 8/81 = 0,0095238+0,0987654 = 0,1082892

4.С.в. распределена по равномерному закону на отрезке . Найти вероятности событий .

P(X>0) = 7/8

P(2<X<7) = 5/8

P(X^2<9) = P(-3<X<3) = P(-1<X<3) = 4/8 = 0.5

P(3X<8) = P(X<8/3) = (10/3)/8 = 10/24 = 5/12

5.Бросают игральный кубик. Найдите условную вероятность выпадения нечетной цифры, при условии, что выпала цифра, большая 3.

Условие: выпало 4,5 или 6. Должна выпасть нечётная: 5. Значит, условная вероятность равна 1/3.

04

1.По каким формулам считается математическое ожидание и дисперсия с.в. , распределенной по биномиальному закону с параметрами .

1а. ;

2.Опишите формулу произведения для трех событий.

Формула произведения для трёх событий: .

3.В урне три белых шара, три черных и три красных, все шары кроме цвета ничем более не отличаются. Берут сразу три шара. Какова вероятность того, что все они а) одного цвета; б) разного цвета.

А) P = (C^3_3 + C^3_3 + C^3_3)/C^3_9

Б) P = (C^1_3*C^1_3*C^1_3)/C^3_9

4.Бросают одновременно два игральных кубика. Найдите условную вероятность того, что сумма выпавших очков больше 10 при условии, что произведение выпавших очков не меньше 10.

Условие: произведение выпавших очков больше или равно 10, т.е. возможны варианты (16 штук):

2-5, 2-6, 3-4, 3-5, 3-6, 4-3, 4-4, 4-5, 4-6, 5-2, 5-3, 5-4, 5-5, 5-6, 6-6, 6-5

Подходящие нам варианты (сумма больше 10):

5-6, 6-6, 6-5.

Итого: вероятность: 3/16.

5.С.в. имеет ряд распределения: . Найдите вероятности событий , зависимы ли первые два события?

P(X>6) = 0 (т.к. значения больше 6 случайная величина Х не может принимать).

P(1<X<7) = 0,2+0,1+0,5 (т.к. в указанном интервале случаяная величина может принимать только значения 2, 4 и 6).

P(X<20) = 1

З(X> -2) = 1

05

1.Событие называется зависимым от события если

1б.

2.Опишите формулу Байеса и условия ее применимости.

Формула Байеса:

,

где

 — априорная вероятность гипотезы A (смысл такой терминологии см. ниже);

 — вероятность гипотезы A при наступлении события B (апостериорная вероятность);

 — вероятность наступления события B при истинности гипотезы A;

 — полная вероятность наступления события B.

3. Дано . Найти и выяснить, зависимы ли события .

P(A) = 0,84; P(B) = 0,5/0,8 = 5/8 = 0,625

P(A U B) = 0,84+0,625-0,5 = 0,965

P_AB = 0,5/0,625 = 4/5 = 0,8

P(AB) = 0,5 = P(A)*P(B) = 0,84*0,625 = 0,525  зависимы

4.С.в. имеет ряд распределения: . Найти а и р, если .

P = 1-0,5-0,1-0,1 = 0,3

MX = 1*0,5 + 4*0,1 + 5*0,1 + a*0,3 = 3

1,4 + a*0,3 = 3  a = 1,6/0,3 = 5 + 1/3 = 5,33333333…

5.Некто написал 5 адресатам письма, а затем наудачу написал на каждом конверте один из 5 имеющихся у него адресов. Чему равна вероятность, что хотя бы одно письмо попало по назначению?

А = хотя бы одно попало по адресу. Тогда –А = ни одно не попало по адресу.

P(-А) = C^5_5*(4/5)^5 = 1025/3125

 P(A) = 1-1025/3125 = 2100/3125 = 0,672

06

1.Укажите формулы, по которым можно найти математическое ожидание и дисперсию с.в. , распределенной по закону Пуассона с параметром .

1в. ;

2.С.в. имеет ряд распределения .Составить ряд распределения с.в. , с.в. .

X^2: 1 – 0,1

9 – 0,2

25 – 0,2

49 – 0,3

Max{X,5}: 5 – 0,5

7 – 0,3

Вообще задание не совсем корректное, т.к. сумма вероятностей в ряде распределения должна быть равна 1, а в этой задаче: 0,1+0,2+0,2+0,3 = 0,8.

3.Дано . Найти и выяснить, зависимы ли события .

P(A) = 0,8; P(B) = 0,5/0,8 = 5/8 = 0,625

P(A U B) = 0,8+0,625-0,5 = 0,925

P_AB = 0,5/0,625 = 4/5 = 0,8

P(AB) = 0,5 = P(A)*P(B) = 0,8*0,625 = 0,5  независимы

4.Составить ряд распределения с.в., распределенной по биномиальному закону с параметрами .

P(x=0) = C^0_3 * p^0 * q^3 = 1/8

P(x=1) = C^1_3 * p^1 * q^2 = 3/8

P(x=2) = C^2_3 * p^2 * q^1 = 3/8

P(x=3) = C^3_3 * p^3 * q^0 = 1/8

5.В доме 3 совершенно одинаковых и независимо работающих лифта в каждом из трех подъездов, по одному лифту в каждом подъезде. С вероятностью 1/2 ежедневно какой-то из лифтов ломается (другие два в этот день исправны). Какова вероятность, что завтра починки потребует лифт в подъезде №1.

Привет! Тут я выдохся первый раз, пока решал ваши задачки.

07

1.Укажите формулу Байеса

1б.

2.Опишите формулу, невыполнение которой равносильно зависимости событий .

Формула: P(AB) = P(A)*P(B)

3.В автохозяйстве каждое утро случайным образом все имеющиеся 7 машин выстраиваются в колонну. Найти вероятности того, что две конкретные машина: а) окажутся рядом; б) в начале и конце колонны.

А) Р = 1/7 * 1/6 = 1/42

Б) P = 1/7 * 5/6 * 4/5 * ¾ * 3/2 * 1/2 = 1/42

4.С.в. распределена по закону Пуассона с параметром . Найти вероятности событий и определить, зависимы ли эти события.

P(0<X<2) = P(X=1) = 2*e^(-2)

P(0<X<4) = P(X=1 или X = 2 или X = 3) = 2*e^(-2) + 2*e^(-2) + (4*e^(-2))/3

Зависимы

5.В урне лежат 3 шара белых, 3 шара красных и 3 шара черных. Берут сразу 3 шара. Какова вероятность, того что все 3 взятых шара: а) одинакового цвета; б) разного цвета(т.е. среди взятых нет шаров одного цвета); в)среди взятых есть шар белого цвета?

А) P = (C^3_3 + C^3_3 + C^3_3)/C^3_9

Б) P = (C^1_3*C^1_3*C^1_3)/C^3_9

B) P = C^1_3/C^3_9

08

1. Укажите формулу, определяющую функцию распределения вероятности с.в.

1г. .

2.Опишите формулу полной вероятности и условия ее применения.

Пусть дано вероятностное пространство  , и полная группа попарно несовместных событий  , таких что            . Пусть   — интересующее нас событие. Тогда

.

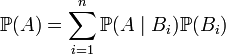3.В аквариуме 3 рыбки простые и 3 золотые. Найти вероятности того, что: а) все простые рыбки окажутся в левой половине аквариума, а золотые в правой; б)все рыбки соберутся в верхей половине аквариума.

А) P = C^3_6*(1/2)^6 = 20/64 = 5/16

Б) P = C^6_6*(1/2)^6 = 1/64

4.Бросают игральный кубик. Найдите условную вероятность выпадения нечетной цифры, при условии, что выпала цифра, большая 4.

Условие: выпало 5 или 6. Должно выпасть нечётная цифра: 5. Значит, вероятность равна ½.

5. С.в. имеет ряд распределения: . Найдите вероятности и математическое ожидание с.в. .

P(X<8) = 0,1+0,1+0,1+0,2+0,1 = 0,6

P(X>2) = 0,1+0,2+0,1+0,2+0,2 = 0,8

P(X<11) = 1

P_(0<x<4)(3<X<7) = P(3<X<4) = P(X=3,5) = 0,1

MX = 1,5*0,1 + 1*0,1 + 3,5*0,1 + 5,5*0,2 + 7,5*0,1 + 9*0,2 + 9,5*0,2 = 0,15+0,1+0,35+1,1+0,75+1,8+1,9 = 0,6+2,9+2,65=6,15

09

1. Укажите расширенную формулу сложения вероятностей:

1в. ;

2.Опишите функцию Лапласа, ее свойства, начертите ее примерный график.

Функция Лапласа:

График:

• Свойства: Функция ошибок нечётна:

• Для любого комплексного   выполняется где черта обозначает комплексное сопряжение числа  .

• Функция ошибок не может быть представлена через элементарные функции

• Функция ошибок на бесконечности равна единице; однако это справедливо только при приближении к бесконечности по вещественной оси.