Геометрическое определение вероятности

Контрольные вопросы

1. Дайте геометрическое определение вероятности. В каких случаях оно используется?

2. Какими свойствами обладает вероятность?

Упражнения

Лекция

40. В круг радиуса вписан правильный треугольник. Найти вероятность того, что точка, брошенная наудачу в круг, попадет в треугольник.

41. Из интервала выбирают наудачу два числа. Найти вероятность того, что их сумма меньше 3.

42. В круг радиуса вписан квадрат. Найти вероятность того, что точка, брошенная в круг, не попадет в квадрат.

43. Из интервала выбирают наудачу два числа. Найти вероятность того, что их разность меньше 1.

Практика

44. На прямолинейном участке газопровода длиной 80 км произошел разрыв. Какова вероятность того, что разрыв удален от обоих концов участка на расстояние большее 30 км.

45. Быстро вращающийся диск разделен на 6 одинаковых секторов, попеременно окрашенных в красный и белый цвета. По диску произведен выстрел, пуля попала в диск. Найти вероятность того, что пуля попала в один из красных секторов.

46. Наугад берутся два числа из отрезка . Найти вероятность того, что их сумма больше 2, а сумма их квадратов меньше 4.

Домашнее задание

47. В точке С, произвольно расположенной на сетевом кабеле АВ длины 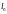, произошел разрыв. Определить вероятность того, что точка С удалена от точки А на расстояние большее 1.

48. На отрезке случайно выбирается точка. Найти вероятность того, что расстояние от неё до правого конца отрезка не превосходит 1,6 единиц.

49. В окружность вписан прямоугольник. Какова вероятность того, что его высота больше длины основания?

50. В окружности радиуса произвольным образом проводится хорда. Какова вероятность того, что длина проведенной хорды меньше радиуса.

51. В круг радиуса R наудачу бросается точка. Какова вероятность того, что точка окажется от центра круга на расстоянии, большем, чем .

52. Внутри квадрата с вершинами 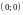, , , наудачу выбирается точка . Найти вероятность того, что длина отрезка меньше 1.

Вероятность сложных событий. Теоремы сложения и умножения вероятностей. Условная вероятность

Контрольные вопросы

1. Какие события называются несовместными?

2. Сформулируйте теорему сложения вероятностей для несовместных событий.

3. Сформулируйте теорему сложения вероятностей для совместных событий.

4. Какое событие называется противоположным событию а?

5. Как вычислить вероятность события , если известна вероятность события А?

6. Дайте определение независимых событий.

7. Сформулируйте теорему умножения вероятностей для независимых событий.

8. Дайте определение зависимых событий.

9. Дайте определение условной вероятности.

Упражнения

Задачи этого раздела необходимо решать с помощью теорем сложения и умножения вероятностей

Лекция

53. Производится стрельба по цели, состоящей из трех непересекающихся зон (концентрических окружностей). Вероятность попадания в I зону составляет , во II – , в III – . Определить вероятность поражения цели.

54. Из урны, содержащей 6 белых, 4 черных и 2 желтых шара, извлекают 3 шара. Найти вероятность того, что все шары одного цвета.

55. Какова вероятность того, что выбранное наудачу трехзначное число делится наудачу на 2 или на 3?

56. В урне 2 белых и 7 черных шаров. Из нее последовательно вынимают наугад два шара. Какова вероятность того, что второй шар окажется белым, при условии, что первым достали черный шар.

57. В коробке 4 белых, 3 синих и 2 черных шара. Наудачу последовательно вынимают 3 шара. Какова вероятность того, что первый шар будет белым, второй – синим и третий – черным?

58. Производится наудачу выбор флага из 4 имеющихся: красного, голубого, белого и трехцветного (красно-бело-голубого). Исследовать на независимость следующие события: – выбранный флаг имеет красный цвет; – выбранный флаг имеет голубой цвет; – выбранный флаг имеет белый цвет.

59. Цифры 1, 2, 3, 4, 5 располагаются в ряд в случайном порядке. Какова вероятность того, что первой окажется четная цифра, а последней – нечетная.

60. В ящике 6 белых и 8 черных шаров. Из ящика последовательно вынули два шара (не возвращая первый шар в урну). Найти вероятность того, что оба шара белые.

61. В урне находятся 10 белых, 15 черных, 20 синих и 25 красных шаров. Вынули один шар. Найти вероятность того, что вынутый шар:

    1. белый или черный;

    2. синий или красный;

    3. белый, синий или черный.

62. Найдите вероятность того, что наугад выбранное трехзначное число делится хотя бы на одно из чисел 4 и 10.

63. На десяти карточках написаны натуральные числа от 1 до 10. Наудачу выбирают последовательно три карточки. Найти:

    1. вероятность того, что второе число нечетное, при условии, что первое число четное;

    2. все три числа нечетные.

Практика