Ф едеральное агентство по образованию фгоу спо «Астраханский государственный политехнический колледж»

«УТВЕРЖДАЮ» Зам. директора по УМР _______________Сорока В.С.

Практикум по дисциплине «Теория вероятностей и математическая статистика»

«Основы теории вероятностей»

для студентов специальностей

230103 «Автоматизированные системы обработки информации и управления»

230105 «Программное обеспечение вычислительной техники и автоматизированных систем»

Астрахань

2010

СЛУЧАЙНЕЕ СОБЫТИЯ. ОПЕРАЦИИ НАД СОБЫТИЯМИ

Контрольные вопросы

1. Какие события называются случайными (приведите пример)?

2. Что называют элементарным событием (приведите пример)?

3. Сформулируйте определение пространства элементарных событий (приведите пример).

4. Какие события называются благоприятствующими событию А (приведите пример)?

5. Какое событие называется достоверным (приведите пример)?

6. Какое событие называется невозможным (приведите пример)?

7. Какие события называются совместными (приведите пример)?

8. Какие события называются несовместными (приведите пример)?

9. Что называют полной группой событий (приведите пример)?

10. Какие события называются равновозможными?

11. Что называют суммой событий (приведите пример)?

12. Что называют разностью событий (приведите пример)?

13. Что называют произведением событий (приведите пример)?

14. Какое событие называется противоположным событию А?

Упражнения

Лекция

1. Укажите пространства элементарных событий для следующих испытаний:

   1. производится выстрел по мишени, представляющей собой 10 концентрических кругов, занумерованных числами от 1 до 10;

   2. проводится турнирный футбольный матч между двумя командами.

2. Сколько элементарных событий содержит каждое из следующих случайных событий, перечислите все элементарные события:

   1. сумма двух наудачу выбранных однозначных положительных чисел равна 12;

   2. число очков, выпавшее на верхней грани игрального кубика, нечетное;

   3. наудачу вырванный листок из нового календаря високосного года соответствует 30 числу.

3. Укажите, какие из следующих событий являются: 1) случайными; 2) достоверными; 3) невозможными.

   1. выигрыш по одному билету лотереи;

   2. извлечение из урны цветного шара, если в ней находятся 3 синих и 5 красных шаров;

   3. получение абитуриентом 25 баллов на вступительных экзаменах в институте при сдаче 4 экзаменов, если применяется пятибалльная система оценок;

   4. выпадение не более шести очков на верхней грани игрального кубика.

4. Какие из следующих пар событий являются несовместными:

   1. наудачу выбранное натурально число от 1 до 100 включительно: делится на 10; делиться на 11;

   2. нарушение в работе: первого; второго мотора летящего самолета;

   3. попадание; промах при одном выстреле;

   4. выигрыш; проигрыш в шахматной партии;

   5. наудачу выбранное натуральное число от 1 до 25 включительно является: четным; кратным трем.

Практика

5. Из урны, содержащей шары белого, черного и синего цвета, наудачу извлекают один шар. События и соответственно означают появление белого и черного шаров. Что означает событие ?

6. Событие А означает появление шести очков на верхней грани игрального кубика. Что означает событие ?

7. Какие из следующих пар событий противоположны:

   1. экзамен сдан студентом на «отлично»; экзамен сдан студентом на «неудовлетворительно»;

   2. хотя бы одна пуля при двух выстрелах попадает в цель; ни одна из двух пуль при двух выстрелах не попадает в цель;

   3. вынутая наугад кость из полного набора домино –«дубль»; вынутая кость не «дубль».

8. Выбирается один человек из студенческой группы. Какие из следующих событий несовместны, а какие совместны:

   1. А – выбран юноша; В – выбрана девушка;

   2. А – выбран юноша; В – выбран староста группы;

   3. А – выбрана девушка; В – выбран мастер спорта по футболу.

10. Из корзины, содержащей красные, желтые и белые розы, выбирается один цветок. Пусть события А – выбрана красная роза, В –выбрана желтая роза, С – выбрана белая роза. Что означают события:

    1. ;

    2. ;

    3. ;

    4. ;

    5. ;

    6. .

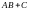11. Из полного набора шахмат выбирается одна фигура ил пешка. Какие из следующих событий являются следствиями других:

    1. А – выбран король; В – выбрана фигура;

    2. А – выбрана черная фигура; В – выбран черный король.

Домашняя самостоятельная работа

12. Имеется 100 жетонов, занумерованных целыми числами от 1 до 100. Событие А – извлечение жетона, номер которого кратен двум, а событие В – извлечение жетона, номер которого кратен пяти. Что означают события:

    1. ;

    2. .

13. Событие А состоит в том, что хотя бы одна из имеющихся 15 электрических лампочек нестандартная. Что означает событие ?

14. Бросается игральная кость. Какие из следующих событий несовместны, а какие совместны:

    1. А – выпало четное число очков; В – выпало нечетное число очков;

    2. А – выпало нечетное число очков; В – выпавшее число очков кратно 3;

    3. А – выпало простое число очков; В – выпало четное число очков.

15. Три студента независимо друг от друга решают одну и ту же задачу. Пусть событие – первый студент решил задачу, – второй студент решил задачу, – третий студент решил задачу. Выразить через события следующие события:

    1. А – все студенты решили задачу;

    2. В – задачу решил только первый студент;

    3. С – задачу решил хотя бы один студент;

    4. D – задачу решил только один студент.

16. Пусть А, В и С – три произвольных события. Выразить через А, В, С и их отрицания следующие события:

    1. произошло только событие С;

    2. произошли все три события;

    3. произошло по крайней мере одно из этих событий;

    4. произошло по крайней мере два события;

    5. произошло только два события;

    6. произошло не более двух событий.