5.1 Операції над нечіткими множинами

Порожня нечітка множина визначається як така, для якої , .

Рівність двох нечітких множин і визначається в такий спосіб. Дві нечітких множини і рівні тоді і тільки тоді, коли рівні їхні функції належності для усіх . Це твердження можна записати в більш компактному вигляді:

Включення нечіткої множини в множину визначається в такий спосіб: ,

Наприклад, нечітка множина довгожителів є підмножиною старих людей.

Нечітка множина називається номінальною тоді і тільки тоді, коли , у протилежному випадку – субнормальною. Непорожні субнормальні множини можна нормалізувати, тобто перетворити їх на номінальну нечітку множину, розділивши на .

Наприклад, нечітка множина старих людей – номінальна множина, тому що точна верхня грань її функції належності дорівнює одиниці:

Розглянемо основні операції на нечітких множинах. Частина цих операцій позначається точно так само як і у випадку класичних, чітких множин. Крім цього операціям на нечітких множинах приписується лінгвістичне тлумачення.

Об'єднання нечітких множин .

Об'єднанням нечітких множин і називається множина функція належності якої дорівнює . Цій операції відповідає висловлення . Це висловлення розкриває лінгвістичний сенс даної операції стосовно нечітких множин. Наприклад, об'єднанням множин «Близько 50» і «Близько 57» буде множина «Близько 50 або 57». Графік функції належності цієї множини приведений на рис. 4.5.

Рисунок 4.5 – Функція належності нечіткої множини «Біля 50 або біля 57»

Перетинання нечітких множин.

Перетинанням нечітких множин і називається множина функція належності якої дорівнює . Цій операції відповідає висловлення «A і B », що розкриває її лінгвістичний сенс. Наприклад, для множин «Старий» і «Немолодий» перетинанням буде множина «Не старий і не молодий». Графік функції цієї множини показаний на рис. 4.6.

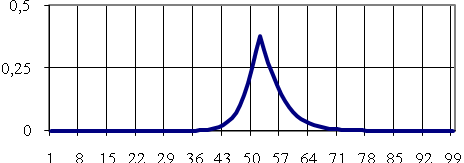
Рисунок 4.6 – Функція належності нечіткої множини «Не старий і не молодий»

Відзначимо, що оскільки функція належності даної множини набуває значення менше одиниці, то вона є субнормальною. Для даної множини . Розділивши на це число, перетворимо дану множину у номінальну. На рис 4.7. приведений графік функції належності нормалізованої множини.

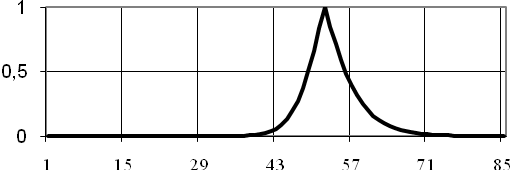
Рисунок 4.7 – Нормалізована множина

Доповнення.

Доповненням нечіткої множини до множини називається множина функція належності якої дорівнює . Лінгвістичний сенс цієї операції визначається висловленням « ». Наприклад, для множини «Старий» доповненням є множина «Нестарий». Графік функції належності цієї множини приведений на рис. 4.8.

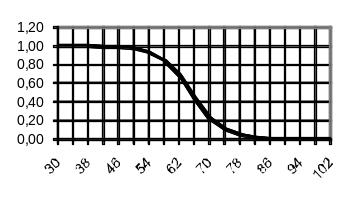
Рисунок 4.8 – Нормалізована множина

Концентрація.

Для нечіткої множини концентрацією є множина функція належності якої визначається зі співвідношення .

Лінгвістичний сенс цієї операції полягає в наступному. Наприклад, для лінгвістичної змінної «старий», концентрація відповідає висловленню «дуже старий». На рис. 4.9 приведені графіки функцій належності нечіткої множини «старий» та її концентрація «дуже старий».

Рисунок 4.9 – Функції належності нечітких множин «старий» та «дуже старий»

Розмивання.

Розмиванням нечіткої множини називається множина функція належності якої визначається зі співвідношення .

Лінгвістичний сенс цієї операції – «не дуже». Наприклад, для лінгвістичної змінної «старий» розмивання – це «не дуже старий». На рис. 4.10 приведені графіки функцій належності для нечітких множин «старий» та її розмивання «не дуже старий».

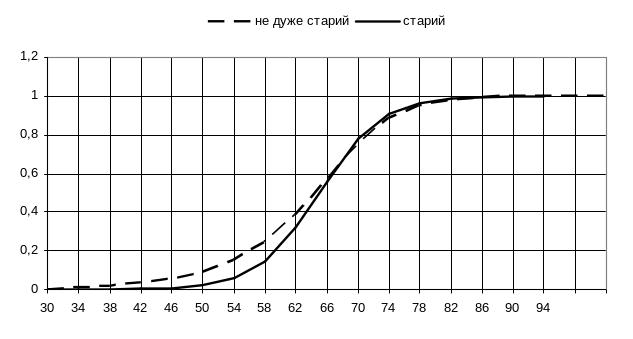
Рисунок 4.10 – Функції належності нечітких множин «старий» та «не дуже старий»

Останні дві операції можуть бути використані тільки до нечітких множин.

На нечітких множинах визначають також операції алгебраїчних добутку та суми. При цьому алгебраїчним добутком нечітких множин та називають множину функція належності якої визначається за формулою

,

а алгебраїчна сума – це множина з функцією належності

.

Операція алгебраїчного добутку дає змогу визначити поняття ступеню нечіткої множини , функція належності якої дорівнює .

Нехай нечіткі підмножини базових множин , відповідно, тоді декартовим (прямим) добутком підмножин будемо називати підмножину множини з функцією належності

.

Декартів або прямий добуток нечітких множин використовується для визначення відношень на нечітких множинах.