5. Нечіткі множини

теорія нечіткий множина логічний вивід

У 1965 р. американський математик Л. Заде опублікував статтю за назвою «Fuzzy sets», що перекладається як «Нечіткі множини». У статті дане нове визначення поняття множини, призначеної для опису і дослідження складних, «погано визначених», «нечітких» систем. У цих системах поряд зі строгими, об'єктивними, кількісними даними і результатами присутні неоднозначні суб'єктивні, якісні дані.

Нечіткість – це така властивість об'єктів або явищ, коли не виконується відношення еквівалентності: об'єкт одночасно може певною мірою належати даній множин, або не належати їй. Невизначеність такого типу описується за допомогою функції належності; значення цієї функції виражає ступінь упевненості, з якою ми відносимо даний об'єкт до зазначеної множини. Сама множина є не обумовленою однозначно і називається нечіткою множиною.

Новий математичний апарат, що ґрунтується на нечітких множинах, використовується для опису властивостей нечітких систем. Викладемо основні поняття теорії нечітких множин.

Нечітка множина складається з невизначеного числа елементів : ознаки, за якими елементи включаються в нечітку множину, не дозволяють однозначно відокремити всі елементи, що їй належать, від елементів, що їй не належать. З нечіткими множинами тісно зв'язане поняття лінгвістичної змінної, уперше введене Л. Заде.

Лінгвістична змінна – це змінна, яка визначається сукупністю вербальних (тобто словесних) характеристик якоїсь властивості. Сформулюємо більш строге визначення цього поняття.

Лінгвістична змінна, згідно Заде, визначається наступним чином:

,

де

– назва лінгвістичної змінної,

– терм-множина її лінгвістичних значень – назв нечітких змінних,

– носій: універсальна множина, яка містить усі можливі результати спостережень або вимірювань, що стосуються досліджуваного об’єкту чи процесу та є областю визначення всіх нечітких змінних,

– синтаксичне правило, яке породжує терми множини Т та включає операції над ними;

– семантичне правило, з використанням якого для кожної нечіткої змінної формується нечітка множина, що є підмножиною носія .

Стосовно нечітких множин, кількісною мірою, що визначає належність елемента множині А є функція належності . Вважається, що для кожного елемента можна задати число , , що виражає ступінь належності цього елемента до нечіткої множини . Якщо , то елемент «чітко» не належить множині А, якщо – «чітко» їй належать. Якщо набуває значення або 0, або 1, то множина , як прийнято говорити, є «чіткою» (класичною) множиною. Характерною ознакою нечіткості множини є наявність хоча б одного елемента з функцією належності, відмінною від 0 або 1. Наведемо визначення нечіткої множини.

Нечітка підмножина множини – це сукупність пар виду (тобто ), де – значення лінгвістичної змінної, – функція, що набуває значення з проміжку [0, 1], .

Функція інтерпретується як ступінь належності елемента множині . Множину – називають ще базовою шкалою лінгвістичної змінної. Функція належності може бути задана аналітично або таблично. Розглянемо найпростіші приклади використання нечітких множин та способи визначення функції належності.

Розглянемо лінгвістичну змінну Вік. Носієм, або базовою шкалою цієї змінної є множина дійсних чисел від 0 до 110 років. Ця змінна може мати, наприклад, такі лінгвістичні значення або терми: дитячий, юнацький, молодий, середній, похилого віку, старий. Ці значення утворюють терм-множину

={ дитячий, юнацький, молодий, старий }.

У якості процедури , що породжує нові терми множини оберемо процедуру з використанням сполучень «і», «або» та модифікаторів «дуже», «не», «трохи» та інших. Наприклад: «дуже старий», «не старий і не молодий». Тоді – це процедура, за якою визначають нечіткі множини, наприклад, – «дуже молодий», – «молодий» тощо.

Визначимо нечітку множину для лінгвістичної або нечіткої змінної «дитячий»: нехай їй відповідає вік що не перевищує, наприклад 10–15 років. Побудуємо відповідну функцію належності. Найпростіше визначити її наступним чином:

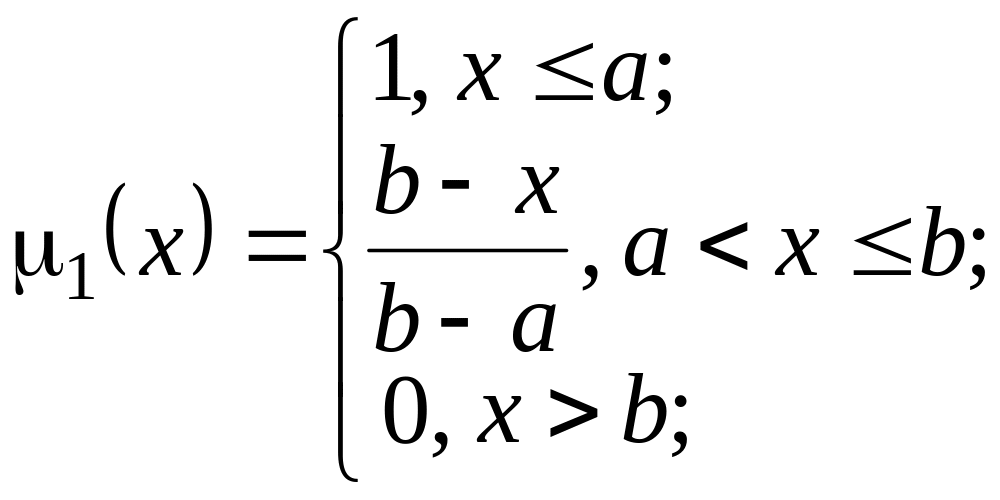
У нашому випадку , а тоді

,

а графік цієї функції буде мати вид такий як показано на рис. 4.1.

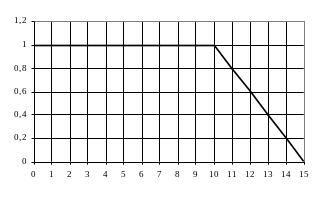
Рисунок 4.1 – Функція належності нечіткої множини «дитячий»

Аналогічним чином побудуємо функцію належності для терму «юнацький». Це нечітка змінна, що має наступне семантичне значення: якщо вік близько 18 років, то це юнацький вік. У цьому випадку функцію належності визначимо за формулою

.

Визначимо коефіцієнти , , , тоді

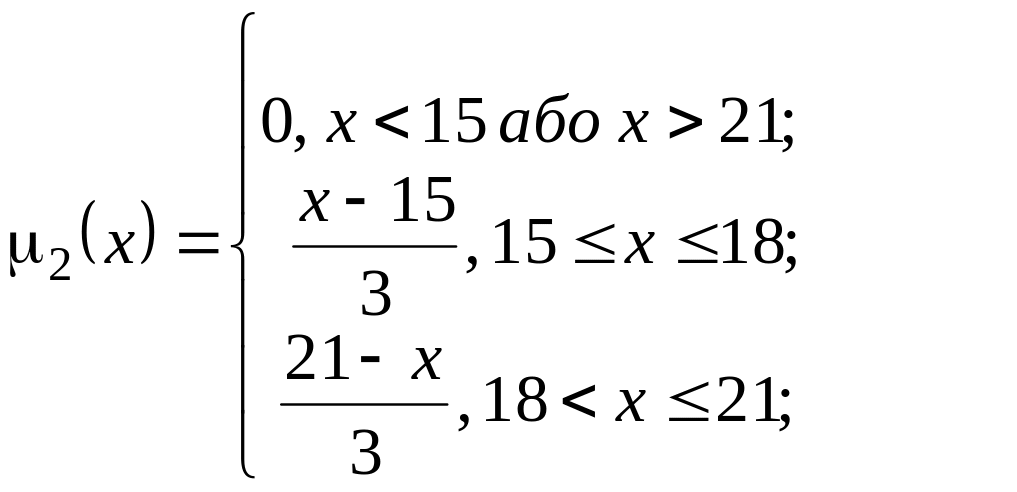
Графік цієї функції наведено на рис. 4.2.

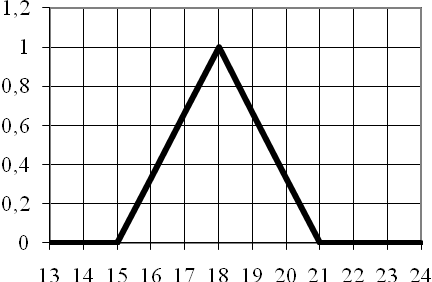
Рисунок 4.2 – Функція належності множини „юнацький”

Подібним чином будуються функції належності і для інших термів лінгвістичної змінної „Вік”.

Розглянемо табличний спосіб завдання функції належності. Розглянемо нечітку множину для терму «трохи». Для цього необхідно з базової шкали, множини натуральних чисел , виділити деяку нечітку підмножину чисел , що відповідають нашому суб'єктивному уявленню про це поняття. Задамо функцію належності множини у вигляді таблиці.

Х	1	2	3	4	5	6	7	8	9	10
	0,0	0,1	0,6	0,8	1,0	1,0	0,9	0,7	0,2	0

Значення функції належності можна інтерпретувати в такий спосіб: число 2 на 10% належить множині , або на 10% відсотків відповідає інтуїтивному поняттю «трохи».

Розглянемо аналітичне визначення функції належності за допомогою неперервної функції. Припустимо, що з множини дійсних чисел необхідно виділити нечітку підмножину , що відповідає інтуїтивному поняттю «близько 50». Очевидно, що у цьому випадку функція належності повинна прямувати до одиниці при , і до нуля – при . Тому для задання скористаємося формулою аналогічною для щільності ймовірності нормального розподілу

.

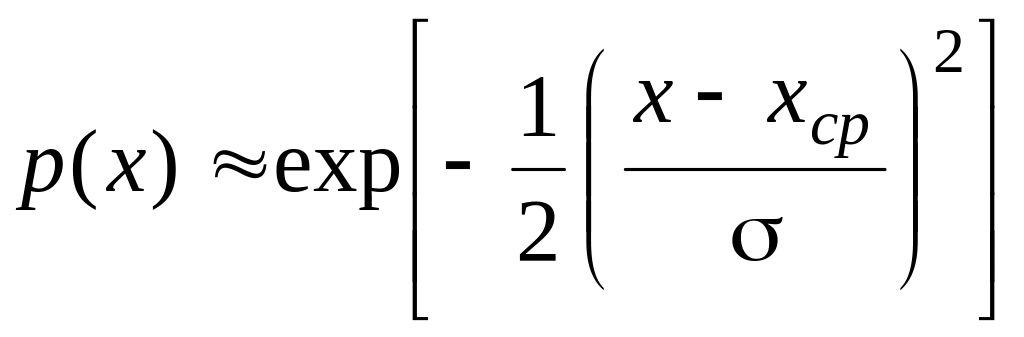Тут – середнє значення випадкової величини, а – дисперсія. Будемо вважати, що поняттю «близько 50» приблизно відповідають числа з діапазону (45,55). Тоді, щоб побудувати функцію належності оберемо = 50, а = 4,5. У результаті отримаємо формулу

.

Н а рис. 4.3 наведений графік .

Рисунок 4.3 – Функція належності множини близько 50

Для функції належності нечіткої множини терму «старий» (позначимо цю множину С) лінгвістичної змінної «Вік» скористаємося наступною функцією:

Тут змінна – це параметр, що враховує суб'єктивність оцінки віку («розмитості» нечіткої множини): чим більший цей параметр тим більше «розмитою» буде множина (рис. 4.4).

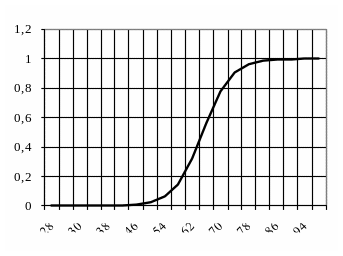
Рисунок 4.4 – Функція належності нечіткої множини «старий»

Найбільш складним у теорії нечітких множин є визначення функції належності. Ще й досі не існує достатньо строгої та формалізованої процедури, використовуючи яку можна було б побудувати функцію належності довільної нечіткої множини. Поки що можна виділити два підходи, стосовно визначення функції належності, та окреслити їх границі.

Перший – прямий підхід застосовується у тому випадку, коли характеристики об’єкту або явища, для яких необхідно побудувати нечітку множину можуть бути виміряні в абсолютній чи відносній шкалі. Прикладом такого підходу є нечіткі множини та їх функції належності, що розглядалися вище. У цьому випадку експерт сам задає значення функції належності для елементів нечіткої множини.

Другий – непрямий, застосовується у випадку, коли характеристики об’єкту або явища, для яких необхідно побудувати нечітку множину можуть бути виміряні в порядковій шкалі чи в шкалі найменувань. У цьому випадку для визначення функції належності залучається група експертів. Кожен експерт шляхом попарних порівнянь визначає значення функції належності для елементів нечіткої множини. Остаточно функція належності встановлюється як узгоджене рішення експертів, шляхом спеціальної обробки їх висновків.