· Сферична система координат

Сферичну систему координат зображено на рис. 17 разом з декартовими осями. Ця система складається з тих самих елементів, що і циліндрична (тобто з осі OZ і перпендикулярної до неї площини). Проте сферичними координатами точки в просторі та її радіус-вектора r є числа (r,q,j). Перше із цих чисел є модулем r, друге – кутом між r і віссю OZ, третє – кутом між і променем полярної системи координат на площині. Щоб встановити однозначну відповідність між точками простору та їх сферичними координатами, встановлюють певні обмеження на значення полярного кута j та азимутального кута q, а саме: вважають, що . Отже, інтервали значень полярного та азимутального кутів різні!

Рис. 17

Координатні поверхні сферичної системи:

– сімейство сфер різних радіусів з центром у точці О;

– сімейство напівконусів з віссю OZ і вершиною в точці О;

– сімейство на півплощин, краєм яких є вісь OZ.

Як випливає з рис. 17 і виразів (5.8), від сферичних координат до декартових треба переходити за формулами:

(5.9)

а від декартових до сферичних – за допомогою формул:

(5.10)

Якобіан переходу

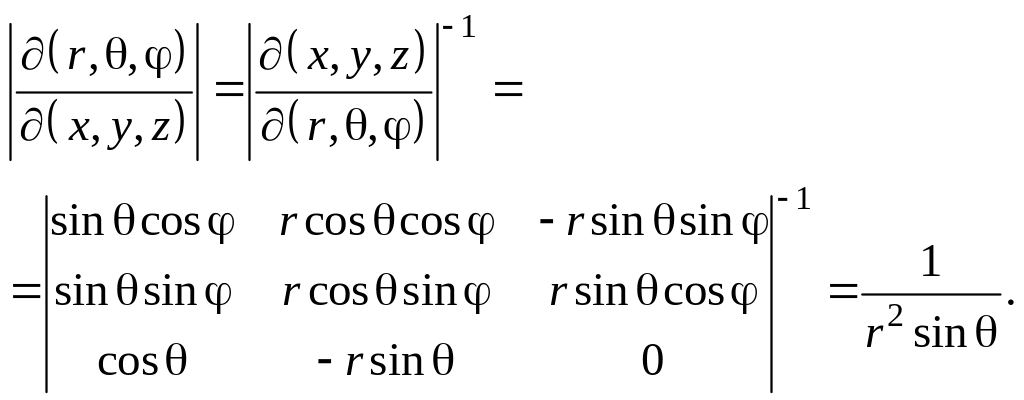
Якобіан не існує для точок осі OZ, на якій порушується взаємно однозначна відповідність точок та їх координат.

5.20. Зауваження. Незважаючи на те, що кути полярної, цилін­дричної та сферичної систем називають координатами, величини q і не є коефіцієнтами розкладів по ортах, на зразок (5.3), (5.4).

§ 39. Локальні базиси криволінійних систем координат

Розглянувши у двох попередніх параграфах декартові системи координат разом з відповідними базисами на площині та у тривимірному просторі, бачимо, що базисні вектори декартових систем напрямлені паралельно до координатних ліній. З огляду на дієвість математичного апарату лінійної алгебри при розв'язанні задач аналітичної геометрії, математичного аналізу та теоретичної фізики, буває доцільно розглядати також базиси, пов'язані з іншими системами координат, такими як полярна, циліндрична, сферична та деякі інші. Однак тоді треба враховувати, що координатні лінії не є прямими, а отже, напрямки базисних ортів можна вважати заданими лише в малому околі кожної точки простору. Базисні орти слід вважати функціями координат просторової точки.

Будемо, як і раніше, пов'язувати з кожною точкою певної області тривимірного простору радіус-вектор r і характеризувати положення точки координатами цього вектора у криволінійній системі координат. Вважатимемо, що в області тривимірного простору існує ненульовий якобіан переходу від криволінійних координат до прямокутних декартових, завдяки чому можна знайти функції та і виразити радіус-вектор будь-якої точки як

(5.11)

(Тут і надалі, якщо не обумовлено щось інше, будемо вважати, що координатні індекси набувають значень 1, 2, 3).

5.21. Означення. Векторами локального контраваріантного базису криволінійної системи координат в області називають величини

(5.12)

5.22. Наслідок. Величини та є координатами векторів контраваріантного локального базису в прямокутній декартовій системі.

5.23. Зауваження. Як напрямок, так і довжина векторів локального базису змінюються при переході від однієї точки простору до іншої (у цьому і полягає їх "локальність"). Особливо це треба мати на увазі при диференціюванні та інтегруванні функцій від цих векторів.

5.24. Зауваження. За обумовлених вище вихідних припущень означення 5.21 є змістовним, оскільки воно забезпечує лінійну незалежність векторів

& Дійсно, зважаючи на наслідок 5.22, мішаний добуток векторів (5.12) можна виразити у вигляді якобіана

Згідно з вихідним припущенням якобіан

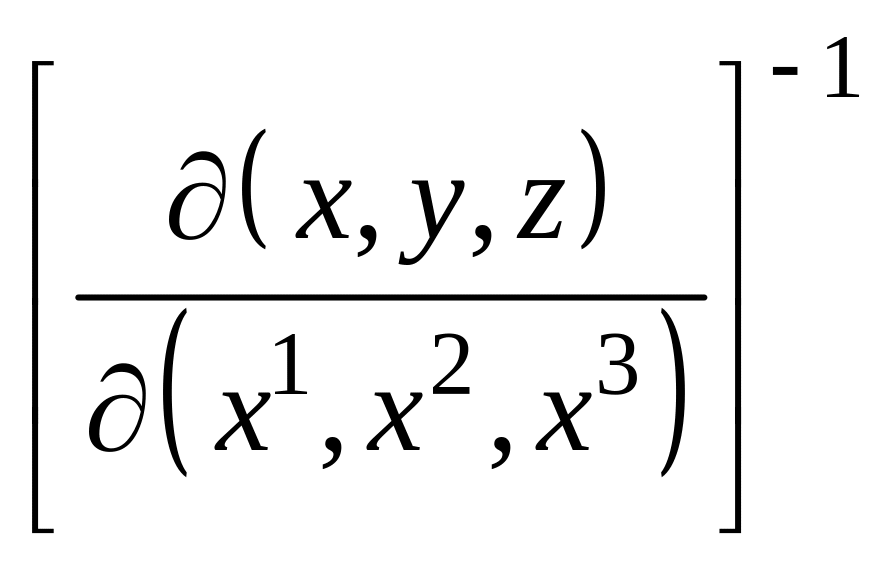
існує, а тому Оскільки мішаний добуток векторів (5.10) не дорівнює нулю, ці вектори некомпланарні, а значить, лінійно незалежні.%

5.25. Зауваження. Вище було враховано, що базисні орти декартової системи є сталими. Оскільки можна позначити та для прямокутної системи координат з (5.10) одержуємо як і має бути.

5.26. Властивість. У кожній точці області базисні вектори дотичні до координатних ліній.

& Безпосередньо випливає з означення 5.21.%

5.27. Означення. Локальним коваріантним базисом називають базис, взаємний до локального контраваріантного базису (див. означення 3.50).

5.28. Наслідок. Величини та є координатами векторів локального коваріантного базису в прямокутній декартовій системі, тобто

(5.13)

& Скалярний добуток двох векторів дорівнює сумі попарних добутків відповідних координат векторів співмножників, тому з (5.12) і (5.13) випливає, що

Отже, тобто вектори (5.13) утворюють базис взаємний до контраваріантного базису і, за означенням, вони є векторами коваріантного базису.%

5.29. Властивість. У кожній точці області базисні вектори перпендикулярні до координатних ліній.

&Безпосередньо випливає з означень 5.27, 3.50 і властивості 5.26.%

Проілюструємо подані вище означення та властивості простим прикладом.

5.30. Приклад. Побудуємо локальні базиси полярної системи координат. Почнемо з контраваріантного базису

Легко впевнитися, що

Вектори коваріантного базису знаходимо з означення коваріантного базису, згідно з яким

Звідси випливає

На рис. 18 показано локальні базиси полярної системи координат у двох різних точках площини. В обох точках А і В базисні вектори і мають одиничну довжину і напрямлені паралельно радіус-векторам цих точок. На відміну від цього, базисні вектори і дотичні до координатних ліній (кіл), що проходять крізь точки А і В. Довжина вектора дорівнює довжині відрізка ОА (для точки А) або ОВ (для точки В). Отже, для А та для В. Оскільки то для А та для В.

Корисно мати на увазі ще деякі властивості та означення, що стосуються локальних базисів і криволінійних координат.

Рис. 18

5.31. Властивість. У кожній точці області справедливі такі співвідношення між векторами коваріантного, контраваріантного та декартового базисів:

(5.14)

& Безпосередньо випливає з (5.12) та (5.13). Наприклад, згідно з (5.12)

Інші співвідношення доводяться аналогічно.%

5.32. Властивість. У кожній точці області справедливі такі співвідношення між векторами двох різних (штрихованого та не­штрихованого) локальних базисів:

(5.15)

& Ці співвідношення читачеві доцільно перевірити самотужки, використавши формули (5.12) і (5.14) для першого з них і формули (5.13) та (5.14) – для другого.%

5.33. Означення. Координатами вектора а з точкою прикладання в області називають коефіцієнти його розкладу за векторами локального базису в цій точці, тобто де – контраваріантні, а – коваріантні координати.

5.34. Властивість. У кожній точці області справедливі такі співвідношення між контраваріантними (коваріантними) і прямо­кутними координатами вектора:

(5.16)

( та x, y, z – криволінійні та декартові координати області ).

& Доведемо першу з двох рівностей. Для цього розкладемо а в коваріантному та декартовому базисах:

Із цих розкладів випливає, що

Зваживши на означення взаємних базисів і формули (5.14) переписуємо останню рівність у вигляді

який і доводить правильність першого зі співвідношень (5.16), оскільки Друге співвідношення доводиться аналогічно.%

5.35. Властивість. У кожній точці області справедливі такі співвідношення між прямокутними та коваріантними (контра варі­антними) координатами вектора

(5.17)

& Ці співвідношення доводяться за допомогою формул (5.16), хід доведення дуже подібний до того, який був використаний для властивості 5.31, тому його переписувати не будемо.%

5.36. Властивість. У кожній точці області справедливі такі співвідношення між координатами вектора у двох різних (штрихованому та нештрихованому) локальних базисах:

(5.18)

& Ці співвідношення доводяться за допомогою формул (5.16) і (5.17)

Друге співвідношення доводиться аналогічно.%