Экономико-математические модели и методы проектного менеджмента

Лабораторная работа № 6. Часть 1

Лабораторная работа № 6. Часть 1 Тема. Простая линейная регрессия

1.1Теоретические сведения

Метод наименьших квадратов (мнк)

 

 

     МНК является классическим методом, с которого надо начинать обзор о методах прогнозирования. Приведено  краткое описание данного метода и показывается, как с помощью его строить прогнозы.

            Пусть в качестве исходных данных имеем таблицу

 

X			…
Y			…

содержащую статистические данные, или данные экспериментов. Если в качестве X выступает время, то имеем динамический ряд (тогда   размещены в возрастающем порядке). Необходимо получить аналитическую зависимость

  ,                                                         (*)

которая наилучшим образом описывает начальные данные. Словосочетание «наилучшим образом», будем понимать в смысле минимума суммы квадратов отклонений значений  , данных в таблице от  , рассчитанных по (*): 

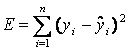
(**) Определение зависимости (*) необходимо, в т.ч., и для нахождения  , что уже представляет собой задачу прогнозирования.

            Нанесём точки из таблицы на координатную плоскость и сделаем предположение, что зависимость (*) есть линейной  , а отклонения от прямой вызваны случайными факторами.

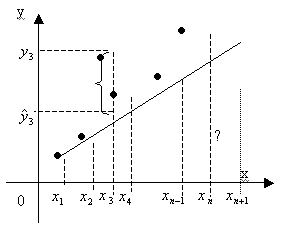
Определим уравнение прямой (найдем значения коэффициентов a и b), так, чтобы получить решение задачи  , т.е. необходимо найти минимум функции

.

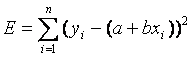Функция . Продифференцируем  по a и по b. Получим:    

 

,

.

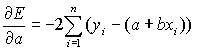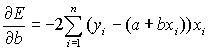Для того, чтобы найти минимум функции E(a,b), приравняем нулю производные и упростим систему:

 

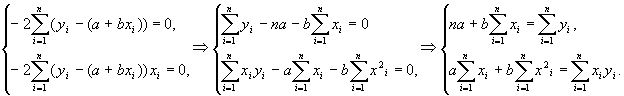
Последнюю систему можно представить в матричном виде:

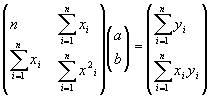
Решая её получим:

          .

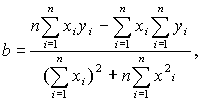
Вычислив a и b, получим функцию , которая в классе линейных функций наилучшим образом описывает табличную зависимость в смысле минимума суммы квадратов отклонений. Теперь можно рассчитать и прогноз

.

Проверка качества описания моделью выборочных данных с помощью коэффициента детерминации

Коэффициент детерминации

где — полная сумма квадратов (total sum of squares),

— сумма квадратов, описанная регрессией (regression sum of squares),

— сумма квадратов ошибок (error sum of squares),

.

Чем ближе коэффициент детерминации к 1, тем лучше модель описывает выборочные данные. Чаще всего (но не всегда!) граничным значением считают величину 0,9. Если коэффициент детерминации близок к нулю, то в выборке отсутствует видимая связь между y и x.

1.2Выполнение работы

1) Найти коэффициенты линейной аппроксимирующей функции y=F(x) для функции y=f(x), которая задана таблицей

xi	yi
1,2	1,1
2,3	2,2
3,8	3,3
4,3	4,4
5,4	5,05
6,3	4,55
7,5	3,75
8,1	2,95
9,6	1,85

• решением системы линейных алгебраических уравнений (СЛАУ);

• найти регрессионную сумму квадратов

• найти остаточную сумму квадратов

• найти коэффициент детерминированности

Аппроксимирующая линейная функция имеет вид y=Bx+A. Для нахождения неизвестных коэффициентов A и B необходимо решить следующую систему уравнений:

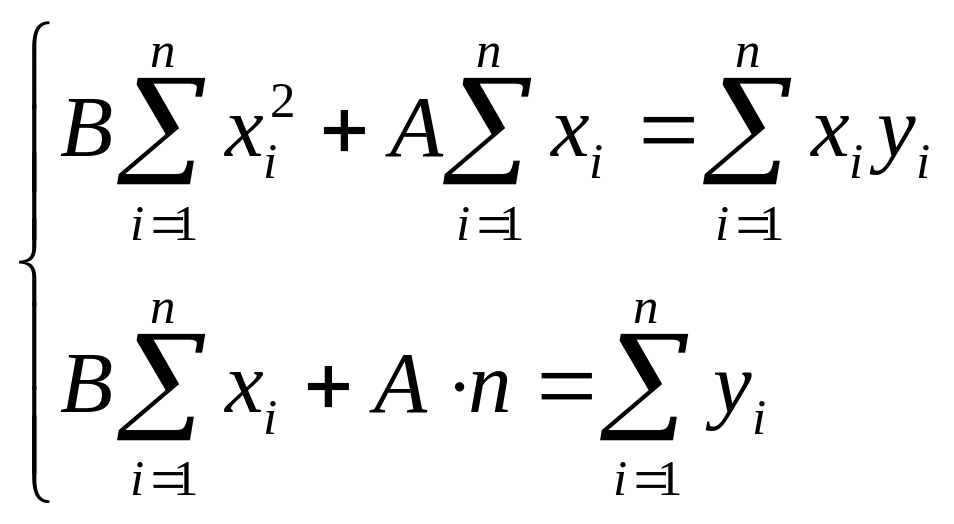
Составим таблицу для вычисления коэффициентов СЛАУ:

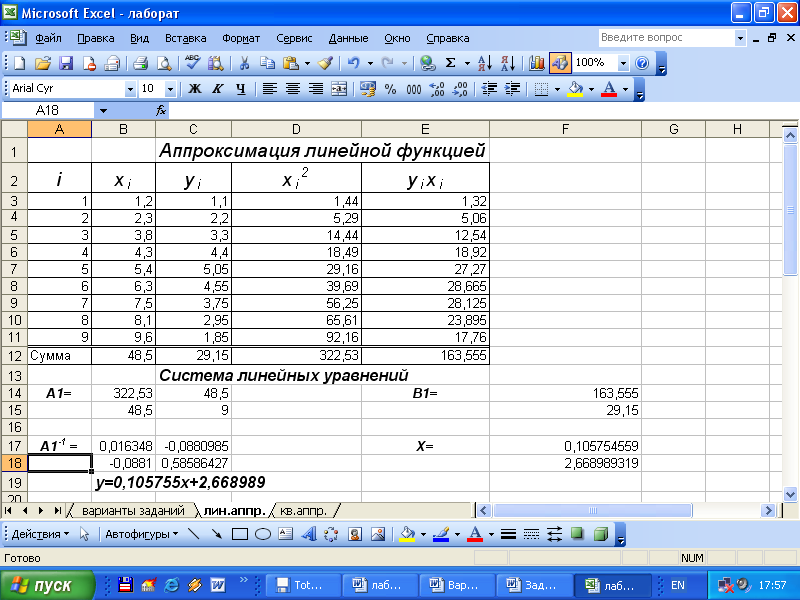
Получим матрицу коэффициентов системы уравнений A1 и столбец правых частей уравнений B1. Полученную систему уравнений

решим методом обратной матрицы. Решение системы – вектор X={x₁,x₂}, где x₁=B, x₂=A

Следовательно, искомая формула имеет вид y=0,105755x+2,668989