18

Міністерство транспорту та зв’язку України Львівський коледж Державного університету інформаційно-комунікаційних технологій

Навчальна дисципліна: Основи схемотехніки

Лабораторія: схемотехніки

Розглянуто Затверджую

на засіданні циклової комісії Заступник директора з НВР

фундаментальних дисциплін ________ Плешівський Я.М.

протокол № 1 від 02. 09.10р.

Голова циклової комісії

_____________ О.І.Лабаз

Інструкція до практичної роботи № 6 Побудова комбінаційного цифрового пристрою в заданому базисі

Склав викладач:

Заліська Н.І.

Львів-2010р.

1. Мета роботи: вивчити принцип функціонування основних логічних елементів, навчитися складати логічні функції комбінаційних цифрових пристроїв (КЦП) та їх мінімізувати, набути практичних навичок з побудови КЦП.

2. Завдання:

   0. 2.1 Скласти таблицю істинності КЦП відповідно до заданого варіанту (табл. 1 додатку).

   1. 2.2 За таблицею істинності записати аналітичний вираз вихідної функції з використанням диз’юнктивної нормальної довершеної форми (ДНДФ) або кон’юнктивної нормальної довершеної форми (КНДФ) відповідно до завдання.

   2. 2.3 Мінімізувати отриманий аналітичний вираз функції з використанням операцій склеювання і поглинання.

   3. 2.4 Скласти карту Карно за таблицею істинності.

   4. За картою Карно записати мінімізовану логічну функцію з використанням ДНДФ або КНДФ відповідно до завдання. Порівняти дану функцію з функцією, що була отримана в п.2.3.

   5. 2.5 Аналітичний вираз, що отриманий в п.2.4, привести до заданого базису з використанням правил алгебри логіки.

   6. 2.6 За отриманим виразом скласти схему КЦП.

   7. 2.7 За довідником вибрати інтегральні схеми для побудови схеми.

   8. 2.7 На основі вибраних інтегральних схем скласти схему електричну принципову КЦП.

3. Теоретичні відомості

Поняття про логічну функцію. Форми представлення логічних функцій

Логічні функції – це функції, що описують роботу цифрових комбінаційних логічних схем, вхідні та вихідні сигнали яких можуть приймати тільки два значення: 0 (логічний 0) та 1 (логічна 1), тобто відповідають двійковій системі числення.

На рис.1 представлена електрична схема, яка складається з двох нормально розімкнутих ключів, електричної лампочки та джерела напруги (батарейки).

Рис.1– Приклади електричних схем з двома ключами.

Кожен з ключів може мати два положення, лампочка має два стани. Для позначення положення ключів та стану лампочки використаємо два символи – 0 і 1. Крім того положення ключа позначимо символом „х”, стан лампочки - символом „f”. Тоді:

Х=0 – ключ розімкнутий; f = 0 – лампочка не горить;

Х=1 – ключ замкнутий; f =1 – лампочка горить.

Логічна функція може бути представлена у двох формах : табличній – у виді таблиці істинності, та аналітичній – за допомогою формули.

В табл.1 приведені логічні функції, які описують роботу схем рис.1 з урахуванням прийнятих вище позначень.

Таблиця 1

№ набору	х2 х1	fа	fб
0	0 0	0	0
1	0 1	0	1
2	1 0	0	1
3	1 1	1	1

Комбінації значень аргументів (х₁, х₂,..., х_n) називають наборами аргументів. Кількість наборів визначається за виразом N=2ⁿ, де n – кількість аргументів. Кількість можливих логічних функцій для n аргументів визначається за виразом M=2^N.

Функція f_а в табл.1 представляє собою логічне множення аргументів (1), а функція f_б – логічне додавання (2):

; (1)

. (2)

Вирази (1) і (2) представляють логічні функції, що задані таблицею істинності (табл.1), в аналітичній формі.

Логічні функції одного аргументу

Комбінації значень аргументів (х₁, х₂,..., х_n) називають наборами аргументів. Кількість наборів визначається за виразом N=2ⁿ, де n – кількість аргументів. Кількість можливих логічних функцій для n аргументів визначається за виразом M = 2^N. Тоді для одного аргументу можна утворити N = 2¹ = 2 набори та скласти M = 2² = 4 логічні функції.

Таблиця істинності для функцій одного аргументу представлена у виді табл.2.

Таблиця 2

Аргумент х	Функції
	f0	f1	f2	f3
0	0	0	1	1
1	0	1	0	1

Функції одного аргументу (табл.2) представляються наступними виразами і називаються:

f₀(х) = 0 - константа 0;

f₁(х) = х - повторення х;

f₂(х) = х - інверсія, логічне заперечення, логічна операція НЕ;

f₃(х) = 1 - константа 1.

Таким чином, з усіх функцій одного аргументу практичний інтерес представляє лише логічна операція НЕ.

Логічні функції двох аргументів

В табл.3 приведені всі можливі функції двох аргументів. Для двох аргументів можна утворити 2² = 4 наборів і відповідно 2⁴ = 16 логічних функцій.

Таблиця 3

№ набору	Аргументи	Функції
	х2 х1	f0	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15
0	0 0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
1	0 1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
2	1 0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
3	1 1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

Функції двох аргументів (табл.3) представляються наступними виразами і називаються:

- кон’юнкція, логічне множення, логічна операція І;

- повторення х₂;

- повторення х₁;

- додавання за модулем 2 (за правилами додавання у двійковій системі числення), функція нерівнозначності, виключаюче АБО;

- диз’юнкція, логічне додавання, логічна операція АБО;

- функція Вебба, заперечення диз’юнкції, логічна операція АБО-НЕ;

- функція рівнозначності (значення функції рівне 1, коли аргументи мають одинакові значення);

- заперечення х₁;

- заперечення х₂;

- функція Шеффера, заперечення кон’юнкції, логічна операція І-НЕ.

Решта функцій представляє менший практичний інтерес.

Логічні вирази розглянутих функцій містять не більше однієї логічної операції, і їх називають елементарними.

Основні правила, тотожності та закони алгебри логіки

В алгебрі логіки, як і взагалі в математиці, прийнятий певний порядок виконання операцій: спочатку виконується операція інверсії (НЕ), потім кон’юнкції (І) і в останню чергу операція диз’юнкції (АБО). Якщо необхідно змінити цей порядок дій, то використовуються дужки. Тоді спочатку виконуються дії в дужках, а потім – поза дужками.

Операції логічного додавання і логічного множення підлягають тим же законам, що і звичайне додавання та множення, а саме:

сполучний закон ;

;

переставний закон ;

;

розподільчий закон ;

.

Можна також привести ряд тотожностей, в справедливості яких легко переконатися, підставивши у ліву та праву частини можливі значення х (0 та 1):

; ;

; ;

; ;

; .

При перетворенні логічних виразів використовуються також так звані правила де Моргана, які дають можливість замінити логічне додавання логічним множенням (диз’юнкцію кон’юнкцією) і навпаки – логічне множення логічним додаванням (кон’юнкцію диз’юнкцією). Для двох аргументів ці правила можна записати так:

; .

Можна сформулювати наступне правило застосування формул де Моргана до складних логічних виразів : інверсія будь-якого складного виразу, в якому аргументи (або їх інверсії) зв’язані операціями кон’юнкції (множення) і диз’юнкції (додавання), може бути представлена тим же виразом без інверсії із зміною всіх знаків кон’юнкції на знаки диз’юнкції, знаків диз’юнкції на знаки кон’юнкції і інверсією всіх аргументів. Наприклад:

.

Представлення логічних функцій в ДНДФ та КНДФ

Існують певні правила, за якими можна за таблицею істинності записати логічну функцію в аналітичній формі. Розглянемо логічну функцію трьох аргументів, задану таблицею істинності (табл.4).

Таблиця 4.

№ набору	Аргументи	Функція
	х3 х2 х1	f(х3,х2,х1)
0	000	1
1	001	0
2	010	1
3	011	0
4	100	1
5	101	0
6	110	1
7	111	1

Використовуються дві форми аналітичного запису логічних функцій: диз’юнктивна нормальна досконала форма (ДНДФ) та кон’юнктивна нормальна досконала форма (КНДФ). Ці форми запису логічних функцій називають канонічними.

ДНДФ логічної функції представляє собою суму конституент 1 для тих наборів аргументів, для яких функція рівна 1. Кожна конституента 1 в свою чергу представляє добуток всіх аргументів (в нашому випадку їх три), але аргументи рівні 0 для даного набору беруться з інверсією. Для заданої функції одиничними наборами є набори 0-ий, 2-ий, 4-ий, 6-ий і 7-ий. Тоді ДНДФ заданої функції буде мати вид:

. (3)

КНДФ логічної функції представляє собою добуток конституент 0 для тих наборів аргументів, для яких функція рівна 0. Кожна конституента 0 в свою чергу представляє суму всіх аргументів (в нашому випадку їх три), але аргументи рівні 1 для даного набору беруться з інверсією. Нульовими наборами для цієї ж функції будуть набори 1-ий, 3-ій, і 5-ий. Відповідно КНДФ заданої функції буде мати вид:

. (4)

Визначення логічного елементу. Умовні графічні позначення логічних елементів

Логічним елементом називають цифровий пристрій, який реалізує елементарну логічну операцію: НЕ, І, АБО, І-НЕ, АБО-НЕ і т.д. Умовні графічні позначення логічних елементів приведені на рис.2.

Значок в лівому куточку умовного позначення вказує на виконувану елементом логічну функцію, значок „° ” на виході логічного елемента означає інверсію сигналу на виході відносно того, який визначається вказаною логічною функцією. Входи логічного елемента можуть бути прямими, як показано на рис.2. Активним рівнем для таких входів є рівень логічної 1. Значком „° ” на вході позначається так званий інверсний вхід, активним рівнем для якого є рівень логічного 0.

Крім простих логічних елементів іноді використовуються складніші. Приклади умовного графічного позначення таких елементів показані на рис.3

Використання логічних елементів для побудови логічних схем

Логічні елементи використовуються для побудови різноманітних цифрових пристроїв. Робота таких пристроїв може бути описана за допомогою логічних функцій. Аналітичний запис логічної функції показує, які логічні операції і в якому порядку треба виконати над аргументами для одержання значення функції. Логічні функції можуть бути реалізовані за допомогою відповідних логічних елементів. Таким чином, логічна функція показує які логічні елементи необхідні для побудови схеми і в якому порядку їх треба з’єднати між собою. Нехай задана логічна функція :

. (5)

НЕ І

АБО

З аналізу виразу (5) видно, що для побудови схеми необхідний один елемент НЕ, один двовходовий елемент І та один двовходовий елемент АБО. Набір елементів, на яких побудована схема, називають базисом. Схема, що побудована за виразом (5), показана на рис.4.

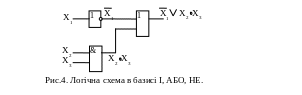
Таблиця істинності комбінаційного цифрового пристрою (КЦП)

Таблиця істинності КЦП представляє собою таблицю, яка містить всі можливі комбінації вхідних сигналів КЦП і відповідні їм значення вихідного (чи вихідних, якщо виходів декілька) сигналу. Складається ця таблиця на основі словесного опису роботи схеми КЦП.

Нехай схема КЦП повинна мати три входи і один вихід. На виході повинен бути сигнал, який відповідає логічній 1, якщо хоча б два вхідні сигнал мають рівень, який відповідає логічній 1.

Кількість наборів вхідних сигналів при трьох входах становить 2³=8. Таблиця істинності матиме вид табл.5

Таблиця 5

№ набору	Х3 Х2 Х1	f
0	0 0 0	0
1	0 0 1	0
2	0 1 0	0
3	0 1 1	1
4	1 0 0	0
5	1 0 1	1
6	1 1 0	1
7	1 1 1	1

На основі таблиці істинності записується вихідна логічна функція КЦП, тобто аналітичний вираз, який описує вихідний сигнал КЦП. Аналітичний вираз може бути представлений у двох формах: ДНДФ (диз’юнктивній нормальній довершеній формі) або КНДФ (кон’юнктивній нормальній довершеній формі).

ДНДФ логічної функції, яка описує вихідний сигнал даної схеми КЦП має вигляд:

(6)

КНДФ логічної функції, яка описує вихідний сигнал даної схеми КЦП має вигляд:

(7)

Мінімізація логічних функцій

Мінімізація вихідної логічної функції. Термін „мінімізація” означає спрощення. Існують різні методи мінімізації логічних функцій. При мінімізації треба пам’ятати закони, правила і тотожності алгебри логіки. Скоротити логічний вираз можна використовуючи дві логічні операції: операцію склеювання і операцію поглинання. Для виконання операції склеювання виявляють у виразі функції пари членів і , які відрізняються лише тим, що один із аргументів в одному із членів представлений без інверсії, а в другому – з інверсією. Дальше проводиться склеювання таких пар членів, яке полягає в тому, що з цих пар виносяться за дужки спільні множники, а сума, яка залишається в дужках перетворюється на 1:

. (8)

Дальше проводиться операція поглинання, яка основана на рівності:

(9)

Ці дві операції повторюються послідовно до тих пір, поки їх виконання виявляється можливим. Розглянемо приклад мінімізації функції, заданої в ДДНФ:

(10)

1 2 3 4 5

Попарним порівнянням членів виразу (10) (кожного з членів з усіма наступними) виявляємо пари, що склеюються: 1-ий і 2-ий; 3-ій і 4-ий; 2-ий і 5-ий (можливі й інші варіанти). В результаті склеювання одержимо:

(11)

Як видно з порівняння виразів (10) і (11), одержаний в результаті перетворення вираз значно простіший, ніж початковий. Отже, і схема побудована за виразом (11) буде значно простіша, ніж побудована за виразом (10).

Мінімізація, що виконана з використанням вказаних вище процедур, вимагає певного досвіду і не може бути зведена до чітко визначених кроків. Її доцільно використовувати лише для достатньо простих логічних виразів.

Мінімізація логічних функцій за допомогою карт Карно

Для мінімізації більш складних виразів можна використати метод карт Карно, який дає чітко сформульовані правила виконання окремих операцій. Карта Карно представляє собою видозмінену таблицю істинності - кожна клітинка карти відповідає одному наборові аргументів. Нехай робота КЦП описується таблицею істинності (табл.6). Цій таблиці відповідає вираз (10).

Табл.7 і табл..8 представляють собою карти Карно для функції трьох аргументів: в табл.2 показано відповідність клітинок карти окремим наборам, а заповнення табл.4 відповідає табл.2.

При мінімізації за допомогою карти Карно об’єднуються сусідні клітинки, які містять 1. Їх можна об’єднувати по 2, по 4, по 8. В результаті об’єднання одержуємо добуток аргументів, спільних для всієї області, причому аргументи рівні нулю беруться з інверсією. Добутки, одержані для окремих областей об’єднання, додаються (виконується операція диз’юнкції).

Таблиця 6 Таблиця 7

х2х1
х3	00	01	11	10
0	000	001	011	010
1	100	101	110	111
Таблиця 8
х 2х1
х3	00	01	11	10
0
1	0		0	0

№ набору	Х3 Х2 Х1	f
0	0 0 0	1
1	0 0 1	1
2	0 1 0	1
3	0 1 1	1
4	1 0 0	0
5	1 0 1	1
6	1 1 0	0
7	1 1 1	0

У нашому випадку для області, яка об’єднує чотири одиниці, спільним буде аргумент Х₃, який треба взяти з інверсією, а для області, яка об’єднує дві одиниці, спільними будуть - Х₁ і Х₂, причому Х₂ треба взяти з інверсією. Таким чином одержимо вираз:

, (12)

Вираз (12) представляє собою мінімальну диз’юнктивну форму логічної функції (МДФ).

В карті Карно можна об’єднувати також сусідні клітинки, які містять нулі, за тими ж правилами, що і клітинки з одиницями (табл..9).

В результаті об’єднання одержуємо суму аргументів, спільних для всієї області, причому аргументи рівні одиниці беруться з інверсією. Суми, одержані для окремих областей об’єднання, перемножуються (виконується операція кон’юнкції) .

Таблиця 9
х 2х1
х3	00	01	11	10
0
1

За табл.9 для першої області (суцільна лінія) спільними будуть аргументи Х₁ і Х₃, причому Х₃ треба взяти з інверсією, а для другої області (пунктирна лінія) - Х₂ і Х₃, причому обидва аргументи треба взяти з інверсією. Таким чином, одержимо вираз:

(13)

Вираз (13) представляє собою мінімальну кон’юнктивну форму логічної функції (МКФ).

Вирази, що одержані в результаті мінімізації методом карт Карно, будуть тим простішими, чим більшими будуть області об’єднання і чим цих областей буде менше.

Мінімізація не повністю заданих функцій

За умовами роботи КЦП може виявитися, що певні комбінації вхідних сигналів є забороненими для даного пристрою і ніколи не можуть виникнути на його входах. Це означає, що логічна функція, яка описує роботу КЦП, не залежить від відповідних комбінацій (наборів) значень аргументів. В цьому випадку функція виявляється заданою не на всіх наборах аргументів, і її називають не повністю заданою.

При синтезі КЦП, який реалізує не повністю задану функцію, можна довільно задати значення функції на наборах, які відповідають забороненим комбінаціям значень сигналів. Ці значення слід задавати так, щоб при мінімізації одержати найпростіший логічний вираз. Таким чином, на заборонених наборах треба задати такі значення функції, при яких в карті Карно клітинки з одиничними (нульовими) значеннями охоплюються мінімальним числом областей з максимальною кількістю клітинок в кожній області. В таблиці істинності довільне (байдуже) значення функції прийнято позначати символом „*”.

Розглянемо приклад такої функції, заданої табл.10, якій відповідає карта Карно у виді табл.11.

Замінюючи зірочки значеннями лог.1 у стрічці для х3=0 і значенням лог.0 для х3=1, отримаємо вираз

. (14)

Таблиця 10 Таблиця 11

х 2х1
х3	00	01	11	10
0
1	0		0	*

№ набору	Х3 Х2 Х1	f
0	0 0 0	*
1	0 0 1	1
2	0 1 0	1
3	0 1 1	*
4	1 0 0	0
5	1 0 1	1
6	1 1 0	*
7	1 1 1	0

Синтез КЦП. Побудова КЦП в базисі І, АБО, НЕ

Під терміном „синтез” комбінаційного цифрового пристрою (КЦП) в даному випадку розуміють його побудову. Схему КЦП легко побудувати, якщо відомий аналітичний вираз логічної функції, яка описує її роботу. Якщо досвід синтезу у розробника невеликий, то можна рекомендувати йому наступну послідовність дій.

Етап 1. Укладання таблиці істинності, яка задає логічну функцію, що описує роботу схеми в табличному виді. При складанні таблиці істинності потрібно проаналізувати значення функції (сигналу на виході КЦП) для кожної комбінації значень аргументів (значень вхідних сигналів).

Етап 2. Запис за таблицю істинності логічної функції в аналітичному виді (в ДДНФ або ДКНФ). Функція, одержана на цьому етапі, може виявитися занадто громіздкою, що приведе до складної логічної схеми КЦП.

Етап 3. Мінімізація вихідної логічної функції одним з розглянутих методів.

Етап 4. Звичайно одержані в результаті мінімізації логічні вирази включають операції І, АБО, НЕ. Отже, на їх основі можна побудувати схему КЦП на логічних елементах І, АБО, НЕ, тобто в базисі І, АБО, НЕ.

Якщо вибраний або заданий інший базис, наприклад, базис І-НЕ чи АБО-НЕ, то одержані в результаті мінімізації логічні вирази треба записати через логічні функції, які відповідають цьому базисові за допомогою правил де Моргана.

Розпишемо логічні функції для виразу (14):

Цей вираз включає логічні операції І, АБО, НЕ. Для побудови відповідної схеми необхідно: два елементи НЕ (для одержання інверсії аргументів х₂ та х₁), один елемент на два входи та один елемент АБО на два входи. Схема, що побудована на основі приведеного виразу показана на рис.5.

Побудова КЦП в базисі І- НЕ

Розглянемо побудову схеми на прикладі виразу (10). Для цього за правилами де Моргана логічну функцію, що виражену через операції І, АБО, НЕ, виразимо лише через одну логічну операцію І-НЕ. Таким чином, виразові (14) буде відповідати вираз (15):

(15)

У виразі (15) фігурує логічна операція НЕ, яка може бути реалізована за допомогою елементу І-НЕ (рис.6) :

1∙X = X

Х

1

&

Рис.6.Реалізація операції НЕ за допомогою елементу І-НЕ

На рис.7 представлена схема КЦП, яка відповідає виразові (15):

Одна стандартна мікросхема містить чотири двовходові елементи. Тому для побудови схем за рис.7 необхідна одна мікросхема, в той час, як для побудови тієї ж схеми за рис.5 треба три мікросхеми, частина елементів яких буде незадіяною.

Побудова КЦП в базисі АБО- НЕ

Розглянемо побудову схеми також на прикладі виразу (14). Для цього за правилами де Моргана логічну функцію, що виражена через операції І, АБО, НЕ, виразимо лише через одну логічну операцію АБО-НЕ. Таким чином, виразові (14) буде відповідати вираз (16):

(16)

У виразі (16) фігурує логічна операція НЕ, яка може бути реалізована за допомогою елементу АБО-НЕ (рис.8).

Х

0vX = X

1

0

Рис.8.Реалізація операції НЕ за допомогою елементу АБО-НЕ

На рис.9 представлена схема КЦП, яка відповідає виразові (16).

Одна стандартна мікросхема містить чотири двовходові елементи. Тому для побудови схем за рис.9 необхідні дві мікросхеми.