§ 5. Потенциал поля точечного заряда и системы зарядов

Для поля точечного заряда точка нулевого потенциала выбирается на бесконечно большом расстоянии r от него. Поскольку интеграл не зависит от формы траектории, будем перемещать единичный пробный заряд вдоль радиуса-вектора:

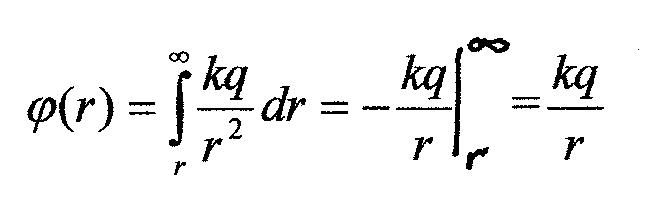
П отенциал системы точечных зарядов.

Пусть заряды-источники находятся на расстояниях от точки наблюдения С. Поскольку в каждой точке поля , то , поэтому потенциал в точке С равен сумме потенциалов, создаваемых в этой точке зарядами :

Это утверждение называют «принципом суперпозиции для потенциала». Поскольку любое заряженное тело конечного размера можно рассматривать как распределение точечных зарядов, оно позволяет рассчитать потенциал создаваемого телом поля (несколько примеров будет рассмотрено чуть позже).

Для графического представления полей, помимо линий напряженности, используют также эквипотенциальные поверхности – геометрическое место точек одинакового потенциала.

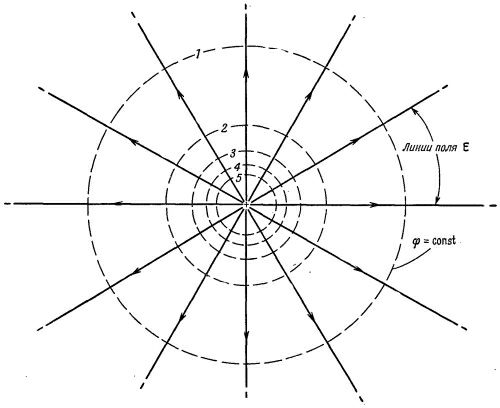
Свойства эквипотенциальных поверхностей:

• Они перпендикулярны линиям напряженности;

• Вектор всегда указывает в сторону убывания потенциала;

• Разность потенциалов для любых двух соседних эквипотенциальных поверхностей должна быть одинакова. Тогда по расположению эквипотенциалей можно судить о величине поля: чем ближе эквипотенциали друг к другу, тем больше напряженность поля.

Демонстрация: эквипотенциальные поверхности

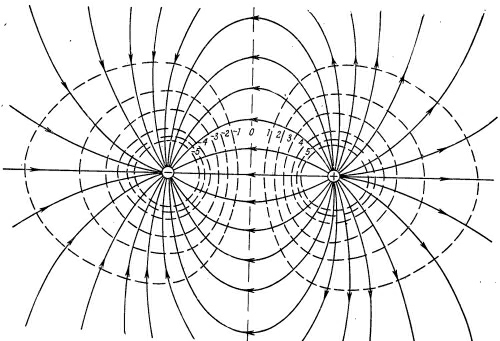
(На этом рисунке эквипотенциали – сплошные линии, пунктир – линии напряженности.)

Примеры расчета потенциала

1. Потенциал на оси заряженного кольца.

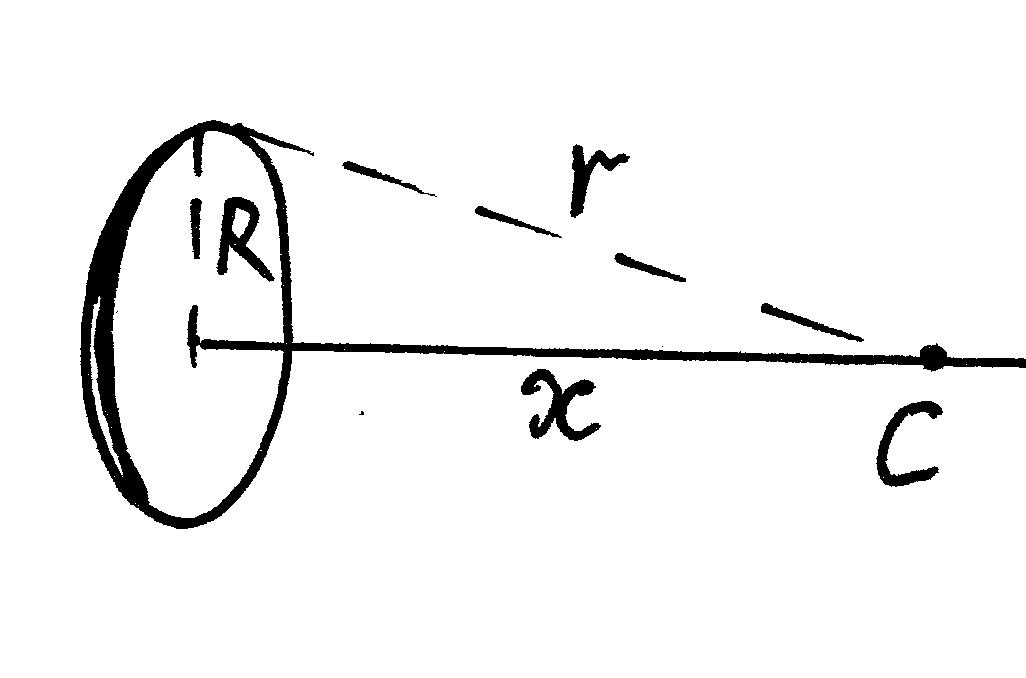Пусть заряд кольца q, радиус R. Найдем потенциал в точке С на оси кольца на расстоянии х от центра.

Разобъем мысленно заряд кольца на бесконечно малые элементы dq. Каждый из них находится на одном и том же расстоянии от точки С и создает в ней потенциал

Суммируя по всем элементам заряда, находим потенциал на оси кольца: .

Этот результат не зависит от того, равномерно или нет распределен заряд по кольцу. Если мы возьмем не замкнутое кольцо, а некий его фрагмент, результат будет тот же! (q – заряд фрагмента).

2. Потенциал заряженной сферы.

Пусть заряд q равномерно распределен по сфере радиуса R.

Мы уже знаем, что внутри сферы , а снаружи ее поле неотличимо от поля точечного заряда q, расположенного в центре.

Выбираем точку нулевого потенциала на бесконечно большом расстоянии от сферы.

Раз снаружи (на расстояниях > от центра) напряженность такая же, как у поля точечного заряда, то и потенциалы этих полей одинаковы:

при .

На поверхности самой сферы .

Внутри сферы , но это не значит, что и !

Е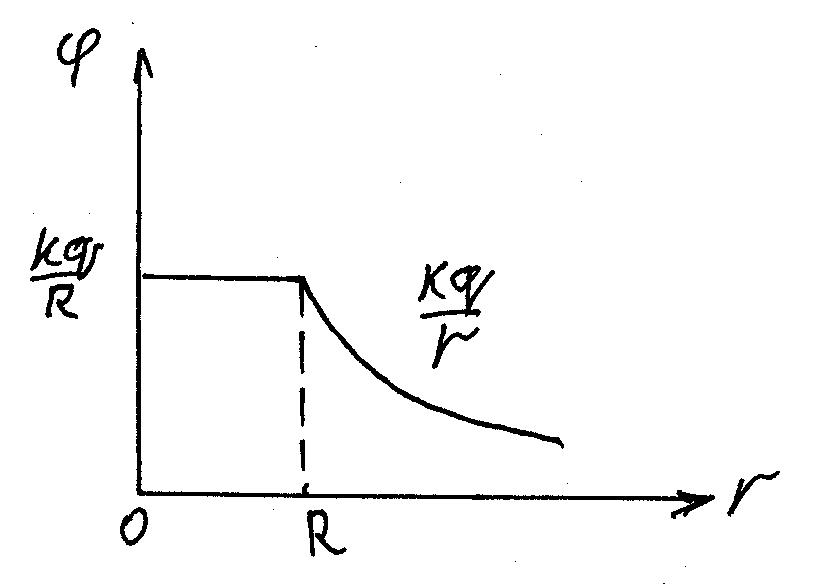 сли в некоторой области пространства электрическое поле отсутствует ( ), потенциал во всех точках этой области один и тот же. Значение потенциала такое же, как на границе области. (См. задачу 1.70) Значение определяется не только полем в данной области, но и во всем пространстве – от данной области до точки нулевого потенциала (бесконечно удаленной).

Внутри сферы потенциал такой же, как на ее поверхности: .

Обратите внимание: потенциал - функция непрерывная. В отличие от напряженности, на заряженной поверхности он имеет не скачок, а излом.