§ 2. Электрическое поле. Напряженность. Принцип суперпозиции полей

Взаимодействие зарядов осуществляется через особую материальную среду – электрическое поле. Заряд изменяет определенным образом свойства окружающего пространства: порождает электрическое поле.

Чтобы установить, имеется ли в данной области пространства электрическое поле, надо поместить туда неподвижный «пробный» заряд (по договорённости, положительный). Сила, действующая на пробный заряд, указывает на существование электрического поля.

Поскольку «пробный» заряд, в свою очередь, воздействует на заряды-источники поля и может вызвать их перераспределение, он должен быть достаточно малым.

Определение. Напряженность в данной точке поля равна отношению силы, действующей на неподвижный положительный пробный заряд q, помещенный в данную точку, к величине этого заряда:

Это отношение не зависит от величины пробного заряда и характеризует электрическое поле в данной точке.

В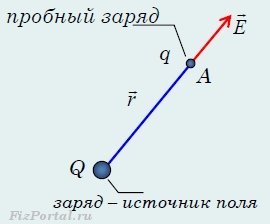 первые идею о том, что пространство вокруг заряженных тел обладает особыми свойствами, высказывал в середине 18 века российский академик Рихман. Через сто лет, примерно с 1830 года, эту идею развивал Фарадей. Сам же термин «поле» ввёл Максвелл в 1865 году.

Фарадей же придумал изображать поле графически с помощью «силовых линий». Сейчас принято называть их «линиями напряженности».

Л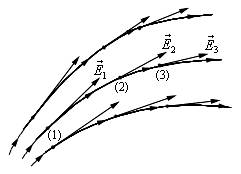 иния напряженности – это линия, касательная к которой в каждой точке совпадает с направлением вектора в этой точке.

Картина линий напряженности позволяет определить направление в каждой точке. Но правильно построенная картина линий напряженности позволяет также сравнивать величину напряженности в разных точках: чем гуще идут линии, тем больше напряженность.

Напряженность поля точечного заряда

Из закона Кулоны следует, что напряженность поля неподвижного точечного заряда q равна

, или . (1)

Картина линий напряженности поля точечного заряда выглядит так:

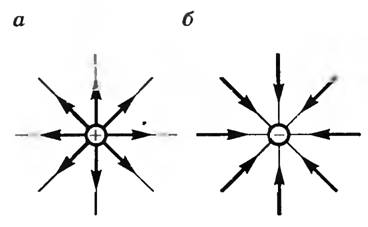
Из принципа суперпозиции сил (установленного на опыте) вытекает принцип суперпозиции полей:

Н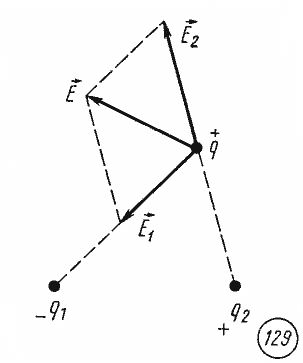 апряженность поля, созданного системой точечных неподвижных зарядов, равна в каждой точке векторной сумме напряженностей полей, создаваемых каждым из зарядов в отдельности:

На рисунке показано, как определить в некоторой точке напряженность поля, создаваемого двумя точечными зарядами:

В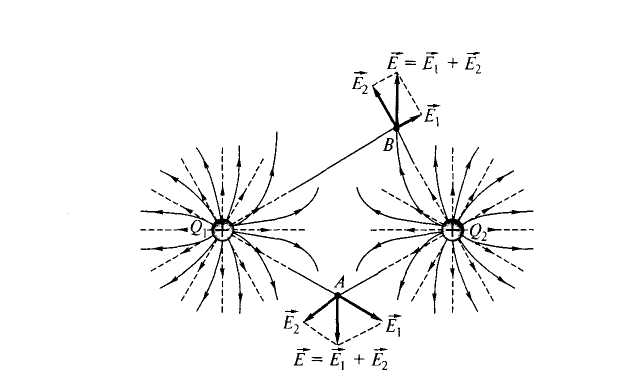 ыполнив такое построение последовательно в нескольких точках, можно домыслить общую картину линий напряженности поля, созданного двумя зарядами. Для двух положительных зарядов получим:

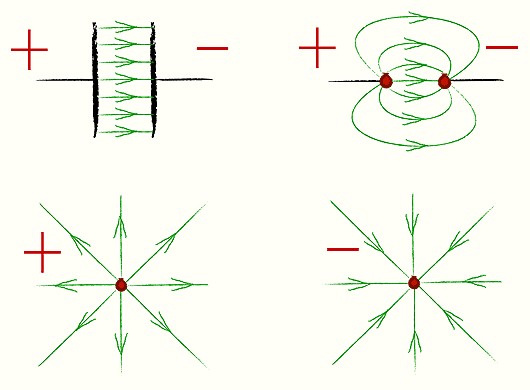
Для разноименных зарядов:

Можно сформулировать общие свойства линий напряженности:

• они начинаются на положительных и заканчиваются на отрицательных зарядах;

• не пересекаются и не касаются друг друга;

• чем гуще линии, тем больше напряженность поля.

Демонстрация. Электрические «султаны» (полоски тонкой бумаги, прикрепленные к металлическим шарикам), заряжаемые от электрофорной машины, позволяют увидеть воочию картину линий напряженности.

С помощью формулы (1) напряженности поля точечного заряда и принципа суперпозиции можно рассчитать напряженность в любой точке поля, созданного любой конфигурацией зарядов.