Задача 4.

Для заданого перерізу (рис.4, табл.4 ) необхідно визначити положення головних центральних осей інерції площі перерізу і визначити величини головних моментів інерції відносно цих осей.

Порядок розрахунку:

1. Накреслити розрахункову схему в масштабі.

2. Провести довільну систему прямокутних координат, нанести центри ваги кожної фігури, визначити положення центру ваги складеного переріза, через який провести центральні осі інерції всього переріза ( і ).

3. Обчислити, використовуючи формули паралельного переносу осей, значення осьових (екваторіальних) і відцентрового моментів інерції , і площі всього перерізу відносно центральних осей.

4. Визначити положення головних центральних осей U і V.

5. Обчислити величину головних моментів інерції відносно головних центральних осей.

6. Перевірити правильність розрахунку.

Таблиця 4

Номер рядка	Схема	Швелер	Кутник рівнобокий	Двотавр
1	I	24	70х70х7	16
2	II	22	80х80х8	18
3	III	30	90х90х8	22
4	IV	20	125х125х12	27
5	V	33	100х100х10	30
6	VI	16	90х90х7	18
7	VII	14	110х110х8	24
8	VIII	36	140х140х12	14
9	IX	18	90х90х7	16
10	X	30	125х125х10	12
	в	а	б	а

Рисунок 4

Рисунок 4

Приклад рішення задачі:

1. Накреслимо в масштабі задану схему складеного перерізу (рис.IV) з позначенням усіх розмірів і осей. Геометричні характеристики складових перерізу такі:

	h, см	в, см	, см	А,
∟ 12,5	12,5	12,5	3,4	22	327	327	520	135
[	22	8,2	2,21	26,7	2110	151	-	-

2. За довільну систему прямокутних координат вибираємо осі Х, У (ця система може бути вибрана і інакше, наприклад ), центри ваги кожної фігури показані на рис.IV.

Визначимо статичні моменти складного перерізу відносно довільних осей Х, У.

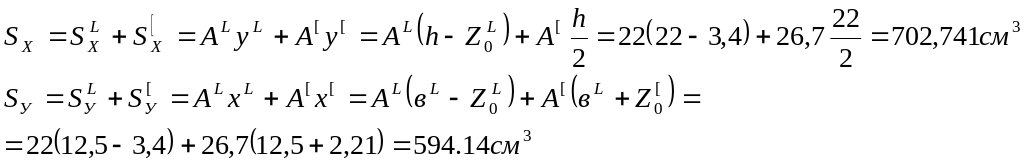
Обчислимо положення центру ваги складного перерізу:

По цим координатам знаходимо в системі довільних осей точку С (центр ваги) і проводимо центральні осі складного перерізу .

3. Обчислюємо значення осьових моментів інерції і відносно центральних осей з урахуванням необхідності паралельного переносу осей.

Значення обчислюються виходячи із розмірів на рис.IV.

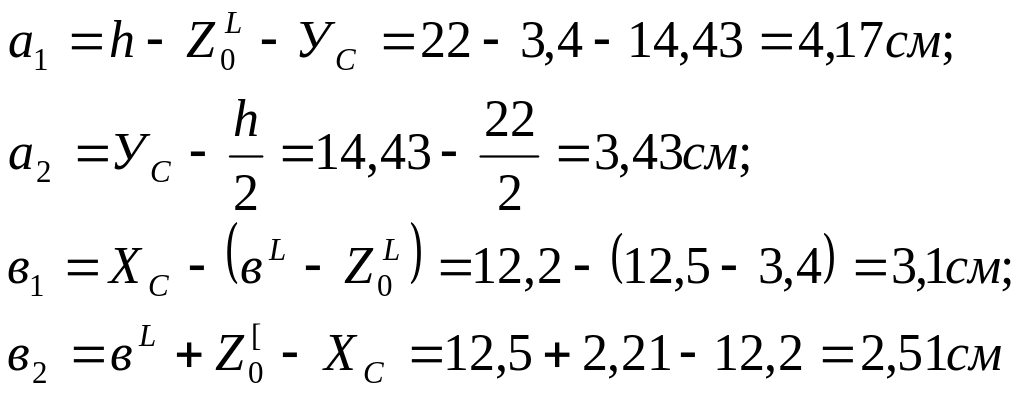
Зауваження: Слід враховувати, що при повороті перерізів на :

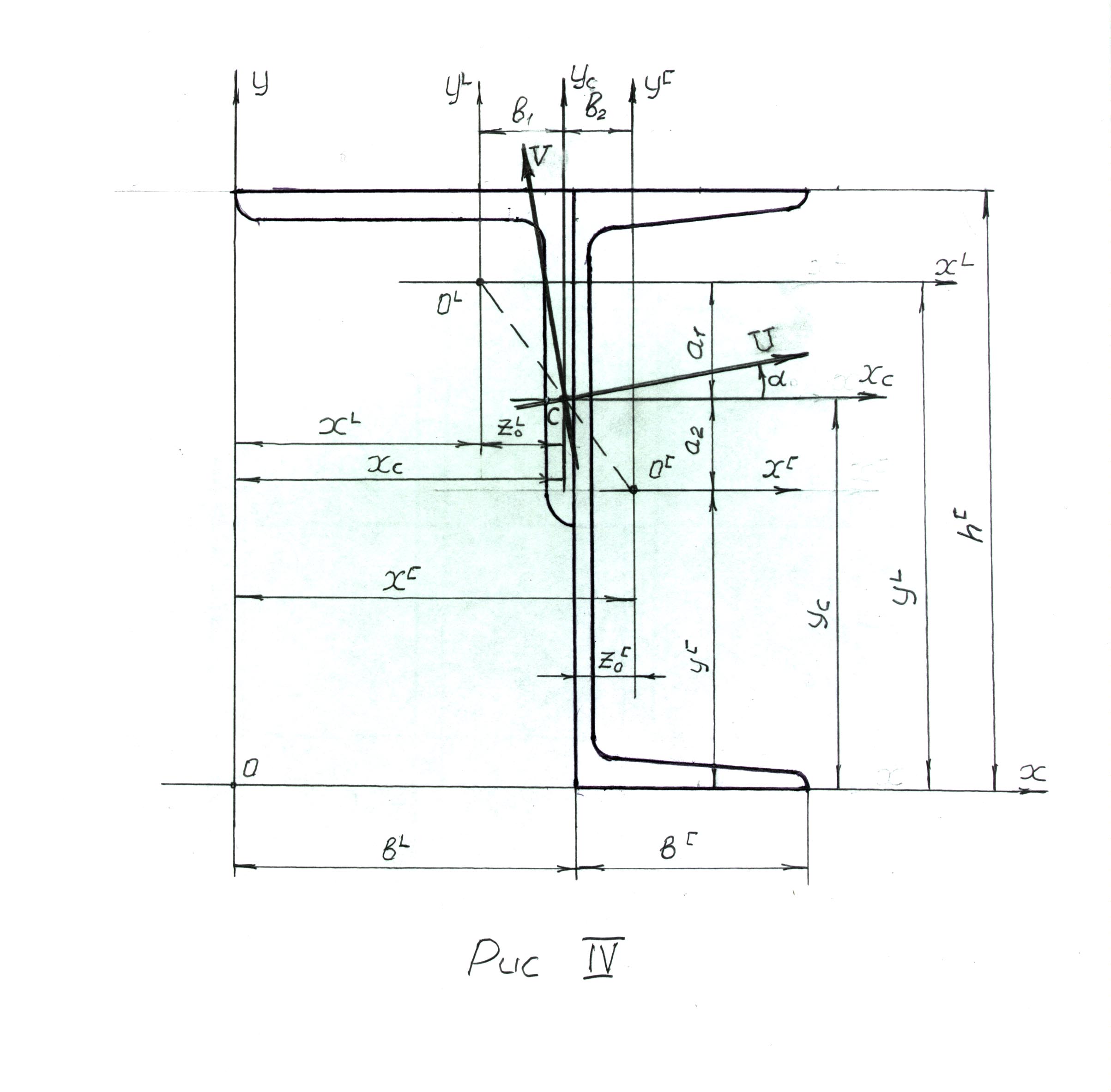Рисунок IV

Обчислюємо значення відцентрового моменту інерції відносно осі з урахуванням необхідності паралельного переносу осей.

Тут:

А. , тому що осі є головними для швелера і відцентровий момент відносно їх дорівнює нулю.

В.

Примітки:

а) Поворот осей проти ходу годинникової стрілки відповідає додатному куту, за годинниковою стрілкою – від’ємному куту.

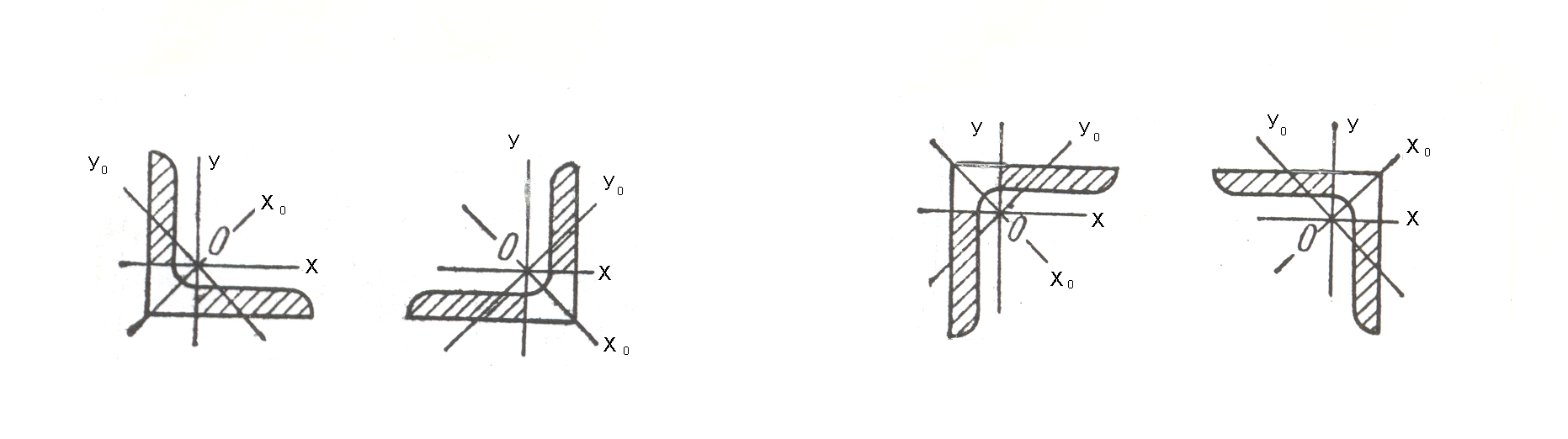
б) При повороті на кут і кутника, відцентровий момент його змінює знак:

;

4. Визначаємо положення головних центральних осей U,V

5. Обчислюємо головні моменти інерції відносно головних центральних осей U і V

6. Перевіримо правильність розрахунків