Задача 2.

Ступінчатий брус (рис.2, табл. 2) знаходиться під дією поздовжньої сили F i власної ваги.

Необхідно: побудувати епюру поздовжньої N сили і нормальних напружень; визначити переміщення перерізу І-І і змінення довжини усього бруса.

Порядок розрахунку:

1. Накреслити в масштабі розрахункову схему.

2. Побудувати епюри поздовжніх N сил і нормальних напружень.

3. Визначити переміщення перерізу І-І

4. Визначити змінення довжини усього бруса

Таблиця 2

Номер рядка	Схема	кН					Матеріал	кН./	МПа
1	I	1,1	2,8	3,2	1,8	12	Ст.3	78,2	2,02
2	II	1,2	2,6	3,0	3,2	14	Мідь	89	1,2
3	III	1,3	2,0	2,6	2,6	10	Латунь	85	0,95
4	IV	1,4	1,0	2,8	2,4	16	Бронза	88,2	1,1
5	V	1,5	2,4	2,4	1,2	12	Алюміній	27	0,69
6	VI	1,6	1,8	2,0	2,4	10	Ст2	78	1,9
7	VII	1,7	1,6	1,8	1,6	18	Сталь легована	78,5	2,1
8	VIII	1,8	1,4	1,2	2,2	20	Бронза Алюмінієва	76	1,05
9	IX	1,9	2,2	1,4	2,0	24	Дуралюмін	28	0,71
10	X	2,0	1,2	1,6	3,0	22	Сталь вуглецева	78	1,9
	в	а	а	в	в	а	б	б	б

Приклад рішення задачі:

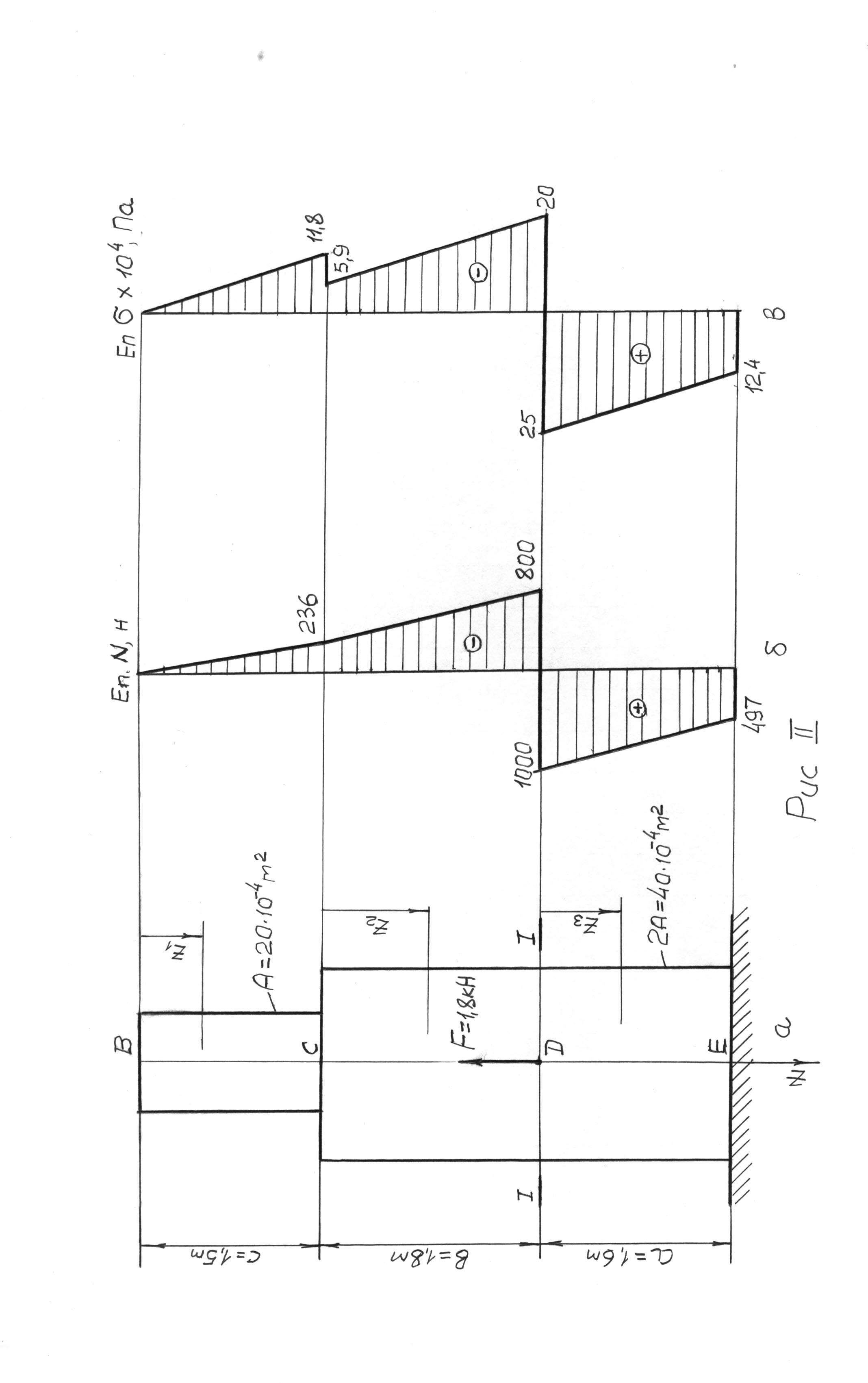
1. Накреслимо в масштабі розрахункову схему бруса (рис.II,а) з позначенням діючих сил і розмірів. Матеріал бруса: сталь легована з питомою вагою

2. Будуємо епюри поздовжніх N сил і нормальних напружень.

Розіб’ємо брус на окремі ділянки. Таких ділянок три : ВС, СD і DЕ. Мислено розрізаємо брус в перерізах Z1, Z2, Z3. Враховуючи вагу вище переріза Zі по методу перерізів напишемо рівняння для поздовжніх N(Zi) сил і нормальних напружень на кожній ділянці.

Перша ділянка (ВС)

В ці рівняння Z1 входить в першій степені, тому на епюрах їх графіком буде пряма похила лінія. Знак „мінус” відповідає деформації стискання.

Друга ділянка (СD);

Слід зауважити, що вага першої ділянки діє на останні ділянки, як зосереджена сила.

Тоді:

Це також лінії похилі до бази епюр.

Третя ділянка (DЕ):

Вага другої ділянки також діє на третю ділянку як зосереджена сила.

Тоді:

Це також лінії похилі до бази епюр.

Епюри поздовжніх N сил і нормальних напружень будуємо по ділянкам бруса, відкладаючи знайдені значення сил і напружень в масштабі по перпендикуляру до бази епюр. За базу приймається лінія, яка паралельна осі бруса (вісь Z, рис.IIа). При цьому ліворуч відкладемо додатні значення і (деформація розтягання), праворуч – від’ємні значення і (деформація стискання). Епюри і наведені на рис.II, б, .

3. Визначаємо переміщення перерізу І-І (рис.IIа)

Деформацію ділянки DE бруса спричинюють сили G1,G2 і F, як зосереджені, а також власна вага бруса ділянки DE. Абсолютна деформація від власної ваги обчислюється по формулі

Тоді, згідно закону Гука маємо:

тут

тобто ділянка DE подовжується.

4. Визначаємо змінення довжини усього бруса.

тобто брус стискається.