Отчет о самоподготовке по ИиКГ

Студента МТУСИ

Группы БРТ 1101

Разоренова Димитрия Проверил: Евстратов П.И.

Кривые линии

Кривая – это множество точек пространства, координаты которых являются функциями одной переменной. Термин «кривая» в разных разделах математики определяется по разному. В начертательной геометрии кривую рассматривают как:

• траекторию, описанную движущейся точкой,

• проекцию другой кривой,

• линию пересечения двух поверхностей.

К ривые бывают пространственные и плоские. Кривая называется плоской, если все ее точки принадлежат некоторой плоскости, в противном случае она называется пространственной.

На ортогональном чертеже кривые линии задают проекциями. При этом, в отличие от задания прямой, необходимо задать по крайне мере проекции одной точки, принадлежащей кривой.

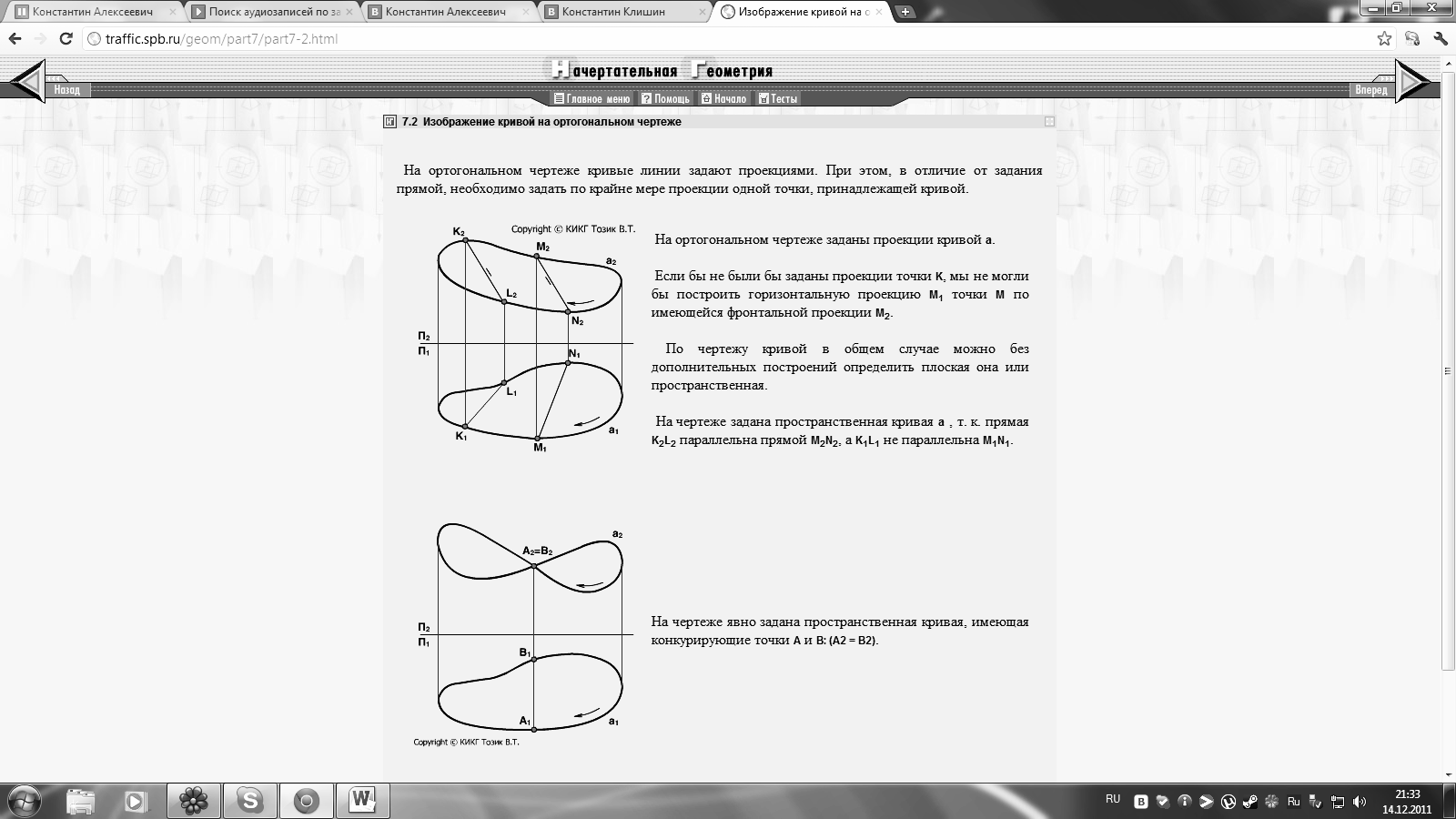  На ортогональном чертеже заданы проекции кривой а.  Если бы не были бы заданы проекции точки K, мы не могли бы построить горизонтальную проекцию M1 точки M по имеющейся фронтальной проекции M2.  По чертежу кривой в общем случае можно без дополнительных построений определить плоская она или пространственная.  На чертеже задана пространственная кривая а , т. к. прямаяK2L2 параллельна прямой M2N2, a K1L1 не параллельна M1N1.

На чертеже явно задана пространственная кривая, имеющая конкурирующие точки А и В: (А2 = В2).

Форма технических объектов нередко содержит плавные переходы. На чертежах переходы изображаются сопряжением окружностей и прямых линий.

Сопряжение – плавный переход с окружности на прямую. Для построения сопряжений необходимо понять логику построения. Основой сопряжений евляются положение о геометрических местах точек. В таблице Геометрические основы сопряжений мы можем наблюдать геомметрические места точек равноудалённых от

1. Концов отрезка,

2. Прямой,

3. Окружности

4. Сторон угла,

5. Точки.

И так мы видим, что ГМТ равноудалённых от концов отрезка, является прямая, Равноудалённых от прямой – две прямые; от окружности – две окружности; От сторон угл – его биссектриса и от точки – окружность.

Построение сопряжений.

1.Сопряжение параллельных прямых. Для построения сопряжений параллельных прямых нужно построить отрезок перпендикулярный обеим прямым так чтобы он был заключён между этими прямыми и через его центр провести окружность радиусом равным половине длинны этого отрезка.

2.Скругление не параллельных прямых. Для этого построения требуется построить две прямые на таком расстояние каков будет радиус скругления и через точку пересечения этих прямых провести полуокружность.

3.Сопряжение окружности и прямой. Для скругления окружности радиусом R окружностью радиусом R2 нужно провести вспомогательную окружность радиусом R+R2 и вспомогательную прямую на расстоянии R2 от данной прямой. Точка пересечения вспомогательной окружности и вспомогательной прямой и есть центр сопрягающей окружности.

4 .Сопряжение двух окружностей. Для построения сопряжения двух окружностей радиусами R и R2 окружностью радиусом R3 нужно провести две вспомогательные окружности из центров данных окружностей радиусами R+R3 и R+R2 соответственно и на точке их пересечения построить сопрягаемую окружность.

Примеры приведены в таблице.

Лекальные кривые.

Лекальными называют плоские кривые, вычерченные с помощью лекал по предварительно построенным точкам. К лекальным кривым относят: эллипс параболу, циклоиду, синусоиду эвольвенту и др.

Д ля построения лекальной кривой сначала на чертеже наносят ряд принадлежащих ей точек, а затем прикладывают лекало.

Э ллипс представляет собой замкнутую плоскую кривую второго порядка. Она характеризуется тем, что сумма расстояний от любой ее точки до двух точек фокусов есть величина постоянная, равная большей оси эллипса. Построить эллипс можно несколькими способами. Например, можно построить эллипс по его большой АВ и малой CD осям. На осях эллипса как на диаметрах строят две окружности, которые можно разделить радиусами на несколько частей. Через точки деления большой окружности проводят прямые, параллельные малой оси эллипса, а через точки деления малой окружности — прямые, параллельные большой оси эллипса. Точки пересечения этих прямых и являются точками эллипса.

Параболой называют незамкнутую кривую второго порядка, все точки которой равно удалены от одной точки — фокуса и от данной прямой — директрисы. Рассмотрим пример построения параболы по ее вершине О и какой-либо точке В. С этой целью строят прямоугольник ОABC и делят его стороны на равные части, из точек деления проводят лучи. В пересечении одноименных лучей получают точки параболы.

Ц иклоидой называют кривую линию, представляющую собой траекторию точки А при перекатывании окружности . Для построения циклоиды от исходного положения точки А откладывают отрезок АА1, отмечают промежуточное положение точки А. Так, в пересечении прямой, проходящей через точку 1, с окружностью, описанной из центра О₁, получают первую точку циклоиды. Соединяя плавной прямой построенные точки, получают циклоиду.

С инусоидой называют плоскую кривую, изображающую изменение синуса в зависимости от изменения его угла. Для построения синусоиды нужно разделить окружность на равные части и на такое же количество равных частей разделить отрезок прямой АВ = 2лR. Из одноименных точек деления провести взаимно перпендикулярные линии, в пересечении которых получают точки, принадлежащие синусоиде.

Э вольвентой называют плоскую кривую, являющуюся траекторией любой точки прямой линии, перекатываемой по окружности без скольжения. Построение эвольвенты выполняют в следующем порядке (рис. 41): окружность делят на равные части; проводят касательные к окружности, направленные в одну сторону и проходящие через каждую точку деления; на касательной, проведенной через последнюю точку деления окружности, откладывают отрезок, равный длине окружности 2лR, который делят на столько же равных частей. На первой касательной откладывают одно деление2лR/n , на второй — два и т. д.

Полученные точки соединяют плавной кривой и получают эвольвенту окружности.

Список литературы:

• Основы инженерной графики В.А. Гервер, А.А. Рывлина, А.М. Тенякшев.

• http://traffic.spb.ru/geom/menu.html

• http://lib.qrz.ru/node/9269

Развёртка поверхности многогранника – это плоская фигура, полученная при совмещении с плоскостью всех его граней.

Определение площади поверхности оказывается полезным при различных покрытиях, выполняемых как с декоративными целями, так и с целью придания поверхности определённых свойств, например повышенной электропроводности, а также при различных химических методах обработки поверхностей.

Построение развертки призматической поверхности можно производить несколькими способами – нормального сечения, треугольников.

При способе нормального сечения построение развертки призматической поверхности целесообразно выполнять в следующем порядке (рис. 6.16):

Пересечь призматическую поверхность вспомогательной плоскостью, перпендикулярной к её ребрам ( Р перпендикулярно 1-2; нормальное сечение);

Развернуть построенную ломаную линию (A₀ B ₀ C ₀ D₀) пересечения вспомогательной плоскости с призматической поверхностью, определив длину её отрезков (A₀B₀ , B₀C₀ , C₀D₀ );

На перпендикулярах к развернутой линии пересечения (A₀D₀) отложить длину отрезков ребер призматической поверхности (A₀2₀ , B₀3₀ , B₀4₀ , C₀5₀ ,C₀6₀ , D₀7₀ ,D₀8₀) и соединить их концы отрезками прямых.

Пример построения развертки боковой поверхности наклонной призмы на чертеже приведен на рисунке 6.17 и 6.18.Для построения вспомогательной плоскости P, перпендикулярной ребрам призмы, выбрана дополнительная плоскость проекций T, параллельная ребрам призмы и перпендикулярная плоскости H. Вспомогательная плоскость Р задана следом Р₁ на плоскости проекций Т перпендикулярно ребрам призмы. Проекции на плоскости Т точек пересечения ребер призмы с плоскостью Р отмечены 1, 2, 3 .На плоскость T боковые ребра призмы проецируются в натуральную величину. Натуральная величина отрезков линии пересечения 1-2-3 плоскостью Р, перпендикулярной ребрам, определена на плоскости S ( пл. S перпендикулярна 7).

По способу треугольников развертка призматической поверхности заключается в следующем: четырехугольники (грани) разбивают диагоналями на треугольники; определяют длины сторон треугольников; выполняют чертеж развертки последовательным построением треугольников, на которые разбиты грани.

Развёртывание боковой поверхности пирамиды

1. Определить длины рёбер и сторон основания пирамиды.

2. П остроить в плоскости чертежа последовательно грани пирамиды (треугольники).

Необходимо найти длину каждого ребра, затем построить треугольник A₀S₀B₀ по трем сторонам: основание А₀В₀ равно горизонтальной проекции А'В', а боковые стороны равны натуральным величинам ребер SA и SB (отрезкам S"A" и S"B").

На стороне S₀B₀ построен второй треугольник, причем сторона В₀С₀ равна горизонтальной проекции В'С, а сторона S₀C₀ равна длине ребра SC (отрезку S"C").

Так же построен и третий треугольник. В результате получена развернутая боковая поверхность пирамиды. (То, что касается сечения пирамиды плоскостью, к алгоритму построения развёртки не имеет отношения).

• Список литературы:

• В.А.Гервер, А.А.Рывлина, А.М.Тенякшев. Основы инженерной графики. Учебное пособие с алгоритмическим представлением графического материала.

• А.А. Чекмарёв. Инженерная графика. Учебник для немашиностроительных специальностей вузов.

• В.О. Гордон, М.А.Семёнцев-Огиевский . Курс начертательной геометрии.

• http://www.nachert.ru

ГОСТ 2.001-93

МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ

ЕДИНАЯ СИСТЕМА КОНСТРУКТОРСКОЙ ДОКУМЕНТАЦИИ

ОСНОВНЫЕ ПОЛОЖЕНИЯ

ОБЩИЕ ПОЛОЖЕНИЯ

1 Разработан Российской Федерацией

ВНЕСЕН Техническим секретарем Межгосударственного совета по стандартизации, метрологии и сертификации

2 ПРИНЯТ Межгосударственным Советом по стандартизации, метрологии и сертификации 17 февраля 1993 г. протокол № 3-93

За принятие стандарта проголосовали:

Наименование государства	Наименование национального органа по стандартизации
Республика Азербайджан	Азгосстандарт
Республика Армения	Армгосстандарт
Республика Беларусь	Белстандарт
Республика Грузия	Грузгосстандарт
Республика Казахстан	Казглавстандарт
Республика Киргизстан	Киргизстандарт
Республика Литва	Литовский Госстандарт
Российская Федерация	Госстандарт России
Республика Таджикистан	Таджикгосстандарт
Республика Туркменистан	Туркменгосстандарт
Республика Узбекистан	Узгосстандарт
Республика Украина	Госстандарт Украины

3 Постановлением Комитета Российской Федерации по стандартизации, метрологии и сертификации от 3 марта 1994 г. № 50 межгосударственный стандарт ГОСТ 2.001-93 введен в действие непосредственно в качестве государственного стандарта Российской Федерации с 1 января 1995 г.

4 ВЗАМЕН ГОСТ 2.001-70

5 ПЕРЕИЗДАНИЕ. Июль 2002 г.

Межгосударственный стандарт Единая система конструкторской документации общие положения

Unified system for design documentation. General principles

Дата введения 1995-01-01

1 Область применения

Настоящий стандарт устанавливает назначение, область распространения, классификацию и правила обозначения межгосударственных стандартов, входящих в комплекс стандартов Единой системы конструкторской документации (ЕСКД), а также порядок их внедрения.

2 Нормативные ссылки

ГОСТ 1.0-92 Правила проведения работ по межгосударственной стандартизации. Общие положения

ГОСТ 2.503-90 ЕСКД. Правила внесения изменений

3 Определение и назначение

3.1 ЕСКД - комплекс стандартов, устанавливающих взаимосвязанные нормы и правила по разработке, оформлению и обращению конструкторской документации*, разрабатываемой и применяемой на всех стадиях жизненного цикла изделия (при проектировании, изготовлении, эксплуатации, ремонте и др.).

* Конструкторская документация является товаром и на нее распространяются все нормативно-правовые акты, как на товарную продукцию.

3.2 Основное назначение стандартов ЕСКД состоит в установлении единых оптимальных правил выполнения, оформления и обращения конструкторской документации, которые обеспечивают:

1) применение современных методов и средств при проектировании изделий;

2) возможность взаимообмена конструкторской документацией без ее переоформления;

3) оптимальную комплектность конструкторской документации;

4) механизацию и автоматизацию обработки конструкторских документов и содержащейся в них информации;

5) высокое качество изделий;

6) наличие в конструкторской документации требований, обеспечивающих безопасность использования изделий для жизни и здоровья потребителей, окружающей среды, а также предотвращение причинения вреда имуществу;

7) возможность расширения унификации и стандартизации при проектировании изделий;

8) возможность проведения сертификации изделий;

9) сокращение сроков и снижение трудоемкости подготовки производства;

10) правильную эксплуатацию изделий;

11) оперативную подготовку документации для быстрой переналадки действующего производства;

12) упрощение форм конструкторских документов и графических изображений;

13) возможность создания единой информационной базы автоматизированных систем (САПР, АСУП и др.);

14) гармонизацию с соответствующими международными стандартами.