ГРАФИЧЕСКАЯ РАБОТА

«СОПРЯЖЕНИЯ, ЛЕКАЛЬНЫЕ КРИВЫЕ»

1 НАЗНАЧЕНИЕ РАБОТЫ

Получение навыков построения лекальных кривых и сопряжений прямых и кривых линий дугами окружностей.

2 СОДЕРЖАНИЕ

2.1 По заданным размерам (варианты индивидуальных заданий даны в приложении) построить детали

2.2 Нанести все необходимые размеры.

3 ОФОРМЛЕНИЕ

Работу выполняют на листе чертежной бумаги формата А3.

В графах основной надписи необходимо указать:

• в графе 1 – наименование работы – «Кулачок»

• в графе 2 – обозначение документа – МКПУ 021103 002

• 03 - номер варианта задания

• В графе 3 – обозначение материала, из которого изготовляется деталь Сталь 45 ГОСТ 1050-78.

Остальное оформление основной надписи соответствует оформлению предыдущих работ.

Толщину линии видимого контура рекомендуется принимать равной от 0,6 до1,0 мм, а остальные линии в два-три раза тоньше.

Все надписи на чертеже и размерные числа выполнить шрифтом 5. Задание выполнить в масштабе 1:1. На чертеже необходимо сохранить все линии вспомогательных построений, изобразить и обозначить точки сопряжений.

4 Теоретические сведения

Под геометрическими построениями понимают элементарные по-

строения на плоскости, в основе которых лежат определенные геометри-

ческие законы.

К геометрическим построениям относят: проведение взаимопер-

пендикулярных и параллельных линий, деление отрезков и углов, вы-

черчивание сопряжений, построение уклона и конусности, построение

алгебраических кривых и многие другие.

Плавный переход одной линии в другую, выполненный при по-

мощи промежуточной линии, называют сопряжением. В инженерной

графике в качестве промежуточной линии чаще всего используют дугу

окружности. Точка, в которой одна линия переходит в другую, называ-

ется точкой сопряжения.

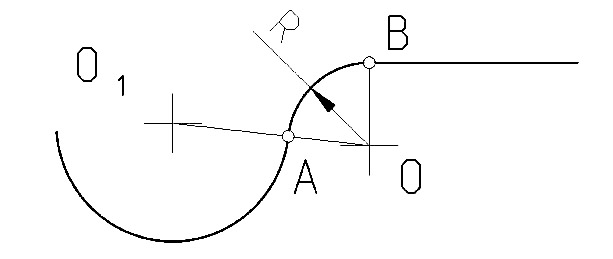
В теории сопряжений применяются следующие термины (рис. 1):

точка О – центр сопряжения; R – радиус сопряжения; точки А и В – точ-

ки сопряжения; дуга АВ – дуга сопряжения.

В основе решения задач на построение сопряжений лежат опреде-

ленные правила:

1. Прямая, касательная к окружности, составляет прямой угол с радиусом, проведенным в точку касания.

2. Геометрическим местом центров окружностей, касательных к данной прямой, является

прямая, параллельная к заданной Рис.1

прямой и отстоящая от нее на величину радиуса окружности.

3. Точка касания двух окружностей (точка сопряжения) находится

на линии, соединяющей их центры.

5 Последовательность выполнения работы

Построение сопряжений включает следующие этапы работы:

1. Строят множество точек (прямую или окружность), находящихся

на расстоянии радиуса сопряжения от первой из сопрягаемых линий.

2. Строят множество точек, находящихся на расстоянии радиуса

сопряжения от второй из сопрягаемых линий.

3. Определяют на пересечении множеств точек центр дуги сопряжения.

4. Определяют точки сопряжения на первой и второй сопрягаемых линиях.

5. Проводят дуги сопряжения в зоне между точками сопряжения.

6 Методические указания

6.1 Построение сопряжений

Плавные переходы широко используют в очертаниях различных технических изделий.

Простейшие сопряжения - плавные переходы прямой линии в дугу окружности или одной дуги в другую. Общая для этих линий точка называется точкой сопряжения.

Непременное условие плавного перехода – общая касательная в точке сопряжения, т.е.переход обеспечивает гладкость первого порядка.

Алгоритм решения задач на построение сопряжений основан на следующих правилах.

Правило 1. Прямая, касательная к окружности, составляет прямой угол с радиусом, проведенным в точку касания.

Правило 2. Геометрическим местом центров окружностей, касательных к данной прямой, является прямая, параллельная заданной прямой и отстоящая от нее на величину радиуса окружности.

Правило 3. Точка касания двух окружностей (точка сопряжения) находится на линии, соединяющей их центры.

6.2 Построение прямой, касательной к окружности

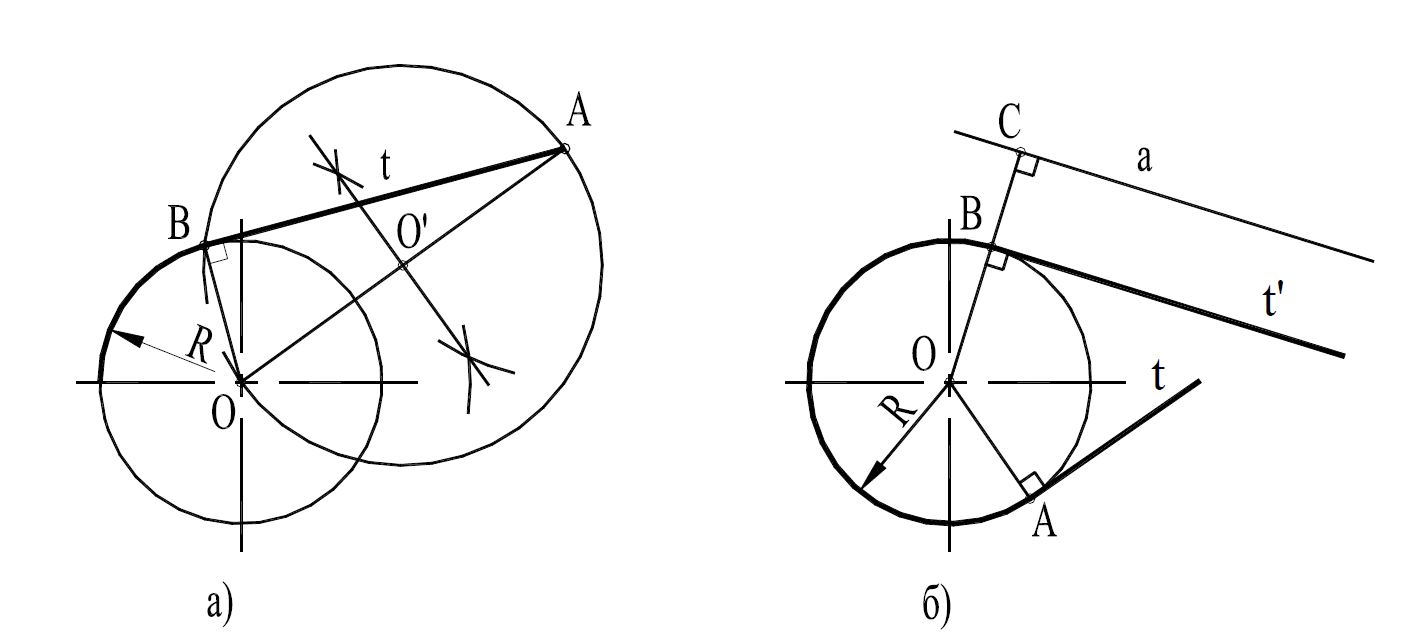Рис.2

Для построения прямой t, проходящей через точку А и касательной к окружности, необходимо соединить центр этой окружности О с точкой А и построить окружность с центром O' на прямой АО и диаметром равным АО (рис.2а). Отмечаем точку В пересечения построенной и заданной окружностей. Соединяем точку В с точками О и А, получаем треугольник АВО. В этом треугольнике угол В прямой, как опирающийся на диаметр окружности. Следовательно катет АВ будет касаться окружности в точке В (правило1).

Для построения прямой t, касающейся окружности в заданной точке А достаточно в соответствии с правилом 1 провести искомую прямую перпендикулярно радиусу ОА (рис.2б).

Для проведения касательной t' к окружности, параллельной заданной прямой а, достаточно найти точку сопряжения В на пересечении заданной окружности с перпендикуляром к прямой, а из центра О: OB ⊥ а, t' ǀǀа, t' ⊥ OB.

6.3 Сопряжение

Примеры построения сопряжений

П р и м е р 1. Сопряжение пересекающихся прямых с помощью

дуги заданного радиуса (рис. 3).

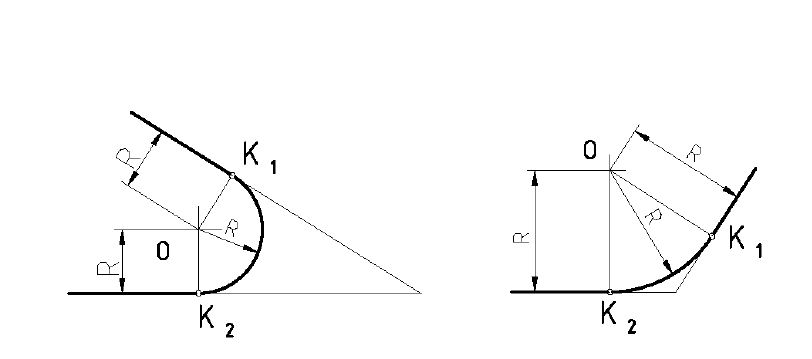
Рис. 3

Для построения сопряжения надо провести прямые, параллельные

сторонам угла на расстоянии R. Из точки О взаимного пересечения этих

прямых (центра сопряжения), опустив перпендикуляры на стороны угла,

получим точки К1 и К 2. Центр сопряжения и точки сопряжения опреде-

ляют радиус сопряжения R. Радиусом R провести дугу.

П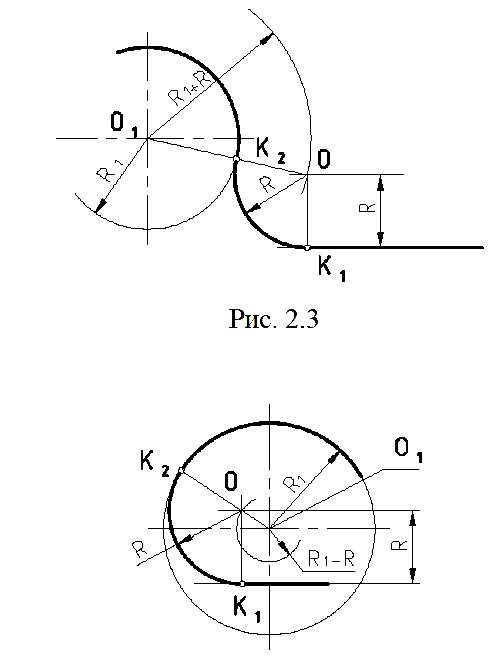 р и м е р 2. Внешнее сопряжение дуги окружности и пря-

мой с помощью дуги сопряжения заданного радиуса R (рис. 4).

На расстоянии R провести прямую, параллельно заданной

прямой, а из центра О1 – дугу окружности радиусом R + R1. Точка О является центром дуги сопряжения.

Точку К1 получим на перпендикуляре, проведенном из точки О на заданную прямую, а Рис.4

точку К2 – на прямой О–О1.

П р и м е р 3. Внутреннее сопряжение окружности и прямой линии дугой заданного радиуса R (рис. 5).

Для построения сопряжения на расстоянии R проводим прямую, параллельную данной, а из центра О1 радиусом R1 – R проводим окружность. Точка О – центр дуги сопряжения. Точку К1 получим на перпендикуляре, проведенном из точки О на заданную прямую, а точку К2 получим на прямой О–О1.

Рис.5

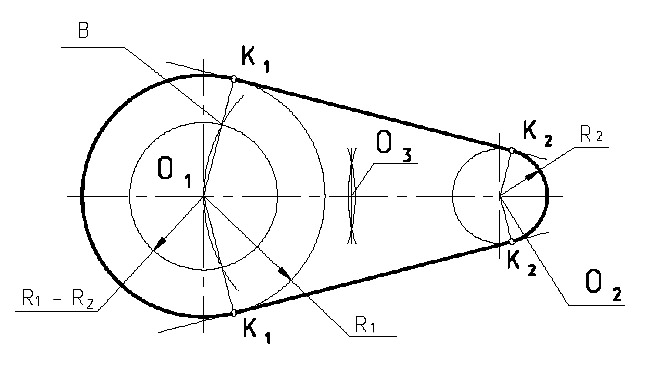
П р и м е р 4. Сопряжение дуг двух окружностей радиусов R1 и R2 прямой линией К1К2 (рис. 6).

Из точки О1 проводим окружность радиусом R1 – R2. Отрезок О1 – О2 делим пополам и из точки О3 проводим дугу радиусом О1 – О3. Эти окружности пересекаются в точке В. Точка В определяет направление перпендикуляра к

касательной К1 – К2 к двум Рис. 6

заданным окружностям.

П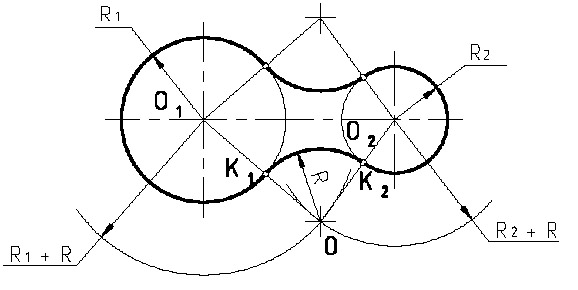 р и м е р 5. Сопряжение дуг двух окружностей радиусов R1 и R2 дугой заданного радиуса R (внешнее сопряжение) (рис. 7).

Из центров О1 и О2 следует провести дуги радиусов R1 + R и R2 + R соответственно. Точка пересечения О этих дуг определяет центр сопряже-

ния. Соединить точки О1 Рис.7

и О2 с точкой О. Точки К1 и К2

являются точками сопряжения.

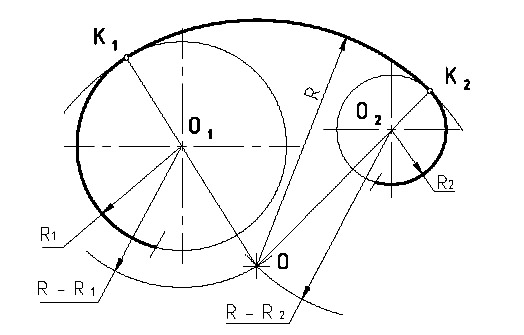
П р и м е р 6. Сопряжение дуг двух окружностей радиусов R1 и R2 дугой заданного радиуса R (внутреннее сопряжение) (рис.8).

И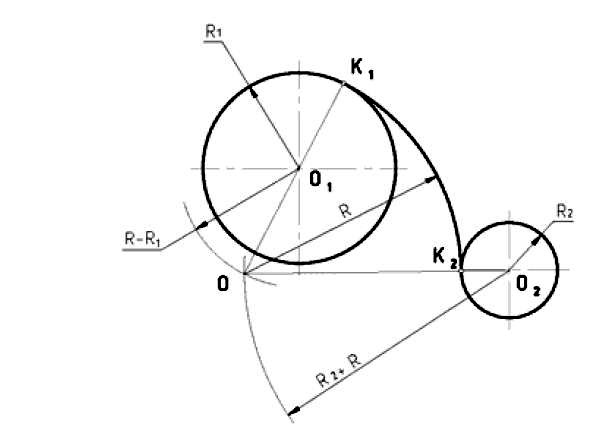 з центров О1 и О2 проводим дуги радиусов R – R1 и R – R2. Получаем точку О, которая является центром дуги сопряжения. Соединяем точки О1 и О2 с точкой О до пересечения с заданными окружностями. Точки К1 и К2 и есть точки сопряжения. Рис.8

П р и м е р 7. Сопряжение дуг двух окружностей радиусов R1 и R2 дугой заданного радиуса R (смешанное сопряжение)(рис.9).

Из центров О1 и О2 нужно провести дуги радиусов R – R1 и R + R2. Точка пересечения дуг О – центр дуги сопряжения. Соединим точку О1 с точкой О и продолжим отрезок до пересечения с окружностью радиуса R1 в точке К1.

Соединив точку О2 с точкой О,определим вторую точку сопря- жения – К2. Рис. 9