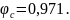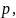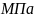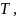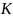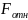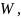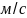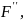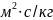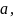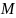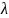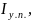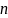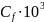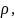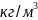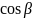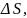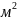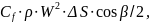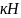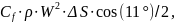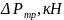- •Содержание
- •9 Выводы. Сравнение результатов проектирования с параметрами
- •Введение
- •1 Задание на проектирование. Исходные данные
- •2 Выбор прототипа проектируемого двигателя. Описание состава и работы схемы пгс жрд на установившемся режиме
- •3 Условная оптимизация соотношения компонентов по максимальному пустотному удельному импульсу
- •3.1 Расчёт стехиометрического соотношения компонентов
- •3.2 Подготовка данных, расчёт и построение графиков в зависимости от и при различных допущениях о равновесности процесса
- •4 Проектирование проточной части сопла
- •4.2 Сопло с профилированной сверхзвуковой частью
- •4.2.1 Профилирование сверхзвуковой части сопла
- •4.2.2 Расчет коэффициента профилированного сопла
- •5 Расчёт основных параметров и размеров камеры двигателя с учётом потерь
- •6 Расчет и построение характеристик камеры
- •6.1 Дроссельные характеристики
- •6.2 Высотные характеристики
- •6.2.1 Высотные характеристики в функции от давления окружающей среды
- •6.2.2 Высотные характеристики в функции высоты полета (глубины хода)
- •7 Расчёт и построение графика распределения равновесных массовых концентраций основных составляющих рабочего тела по длине сопла
- •8 Научно-исследовательская часть проекта. Математическое моделирование предельного влияния скорости химических реакций в рабочем теле
- •8.1 Подготовка данных, расчёт и построение распределения параметров рабочего тела по длине профилированного сопла при различных допущениях о скоростях химических реакций в потоке
- •8.1.1 Равновесное течение
- •8.1.2 Частично замороженное течение
- •8.1.3 Замороженное течение
- •8.2 Анализ особенностей распределения параметров по длине проточной части камеры при разных моделях течения и объяснения причин их появления с учётом изменения состава рабочего тела
- •8.3 Оценка возможных потерь на неравновесность течения в сопле двигателя
- •9 Выводы. Сравнение результатов проектирования с параметрами двигателя - прототипа. Анализ причин рассогласования
- •Литература
4 Проектирование проточной части сопла
Тяга двигателя в
пустоте:
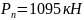
Давление в камере:
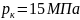
Пустотный удельный
импульс:
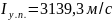
Расход топлива:
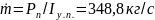
Площадь критического сечения через удельную площадь потока:
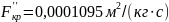
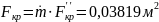
Диаметр критического
сечения:
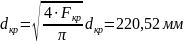
Площадь выходного сечения камеры с насадком через относительную площадь:
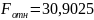
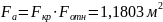
Диаметр
выходного сечения:
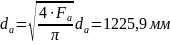
Площадь выходного сечения камеры без насадка через относительную площадь:
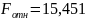
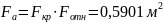
Диаметр
выходного сечения:
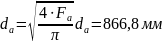
Принимаем отношение
площади камеры сгорания к площади
критического сечения равное 5 (т.к. для
изобарической камеры сгорания
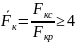 ).
).
Тогда площадь
камеры сгорания равна:
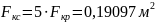
Диаметр камеры
сгорания:
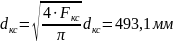
Размеры камеры сгорания определим по формулам [5, стр. 364-366, и 6,стр. 254-255]
Время пребывания компонентов в камере сгорания (выбираем по прототипу)[1]:
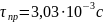
Объем камеры сгорания:
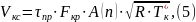
где при
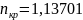 :
:
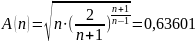
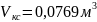
Условная длина камеры сгорания:
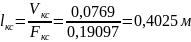
Длина входной части камеры сгорания:
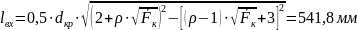
где принимаем
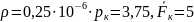 - относительная площадь камеры сгорания;
- относительная площадь камеры сгорания;
Координаты точек сопряжения дуг окружностей:
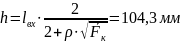
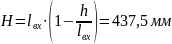
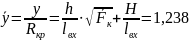
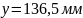
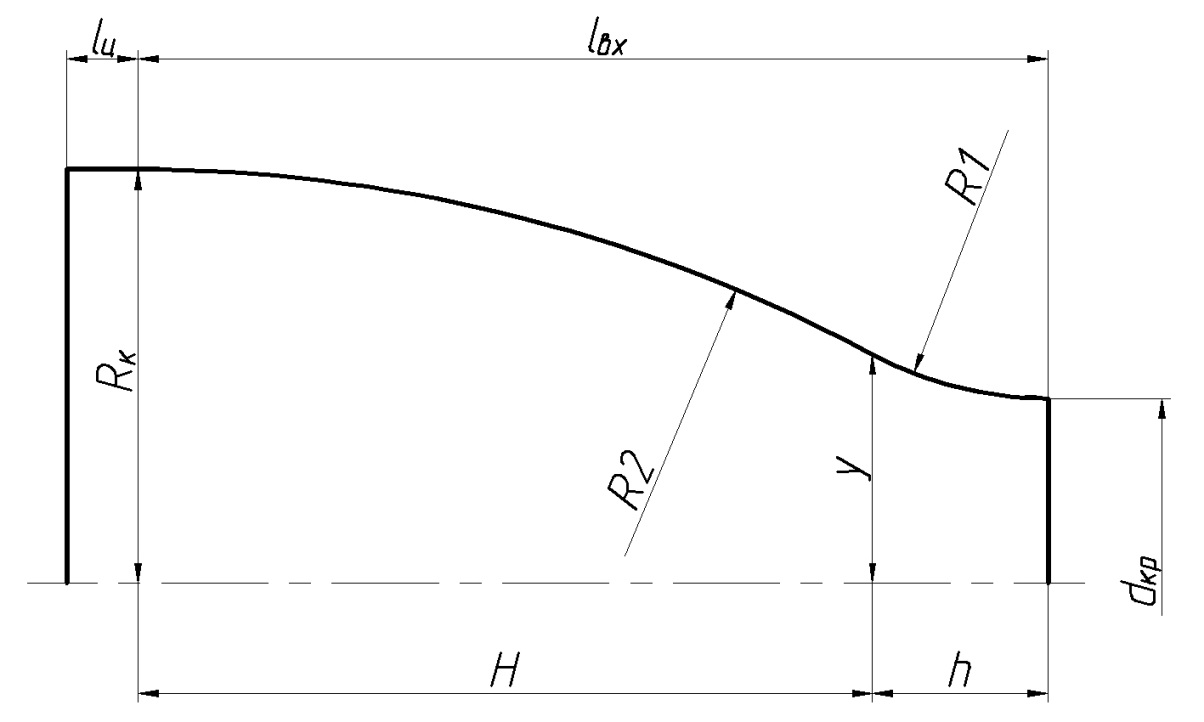
Рис.1. Построение контура камеры сгорания
Объем входной части сопла:
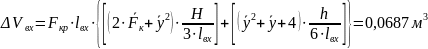
Длина цилиндрической части камеры сгорания:
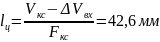
Принимаем следующие размеры камеры сгорания:
Первый сопряженный
радиус
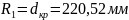
Второй сопряженный
радиус
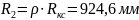
4.1 Сопло с
конической сверхзвуковой частью с
оптимальным углом раскрытия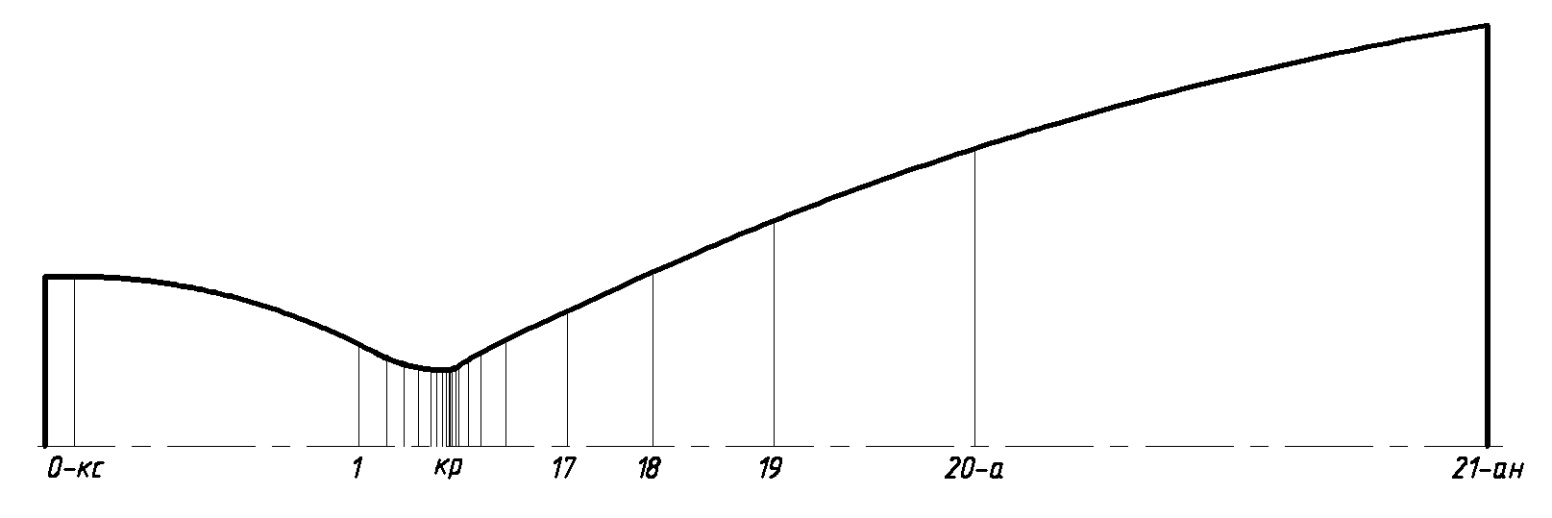
Рис.2. Схема разбиения сопла на участки
Распределение параметров потока по длине проточной части представлено в таблице 4.
Номер сечения |
|
|
|
|
|
|
|
|
|
|
0 - кс |
14,8773 |
3215,12 |
5 |
- |
- |
1113,2 |
0 |
0 |
- |
- |
1 |
14 |
3194,95 |
1,82294 |
387,15 |
0,0001996 |
1109,07 |
0,34908 |
0,3594 |
- |
1,1372 |
2 |
13 |
3170,52 |
1,35411 |
556,29 |
0,0001482 |
1104,07 |
0,503854 |
0,5164 |
- |
1,13731 |
3 |
12 |
3144,33 |
1,16625 |
692,99 |
0,0001277 |
1098,71 |
0,630738 |
0,6433 |
- |
1,13723 |
4 |
11 |
3116,07 |
1,07069 |
814,89 |
0,0001172 |
1092,93 |
0,745603 |
0,7565 |
- |
1,13716 |
5 |
10 |
3085,36 |
1,02122 |
929,07 |
0,0001118 |
1086,65 |
0,854989 |
0,8625 |
- |
1,1371 |
6 |
9,5 |
3068,93 |
1,00812 |
984,60 |
0,0001104 |
1083,29 |
0,908901 |
0,914 |
- |
1,13702 |
7 |
9 |
3051,7 |
1,00132 |
1039,55 |
0,0001096 |
1079,77 |
0,96275 |
0,965 |
- |
1,13705 |
8 - кр |
8,656 |
3039,32 |
1 |
1077,24 |
0,0001095 |
1077,24 |
1 |
1 |
206,491 |
1,13701 |
9 |
8 |
3014,42 |
1,0047 |
1149,15 |
0,00011 |
1072,16 |
1,07182 |
1,0668 |
206,92 |
1,13701 |
10 |
7,5 |
2994,14 |
1,01472 |
1204,28 |
0,0001111 |
1067,96 |
1,12765 |
1,1179 |
207,772 |
1,13698 |
11 |
7 |
2972,59 |
1,03034 |
1260,22 |
0,0001128 |
1063,57 |
1,1849 |
1,1699 |
209,033 |
1,13697 |
12 |
6 |
2924,81 |
1,08103 |
1375,53 |
0,0001183 |
1053,86 |
1,30524 |
1,2769 |
212,683 |
1,13698 |
13 |
5,265 |
2884,69 |
1,13883 |
1464,70 |
0,0001247 |
1045,72 |
1,40067 |
1,3597 |
216,303 |
1,13702 |
Таблица 4. Распределение параметров потока по длине проточной части сопла. Равновесное приближение
Продолжение таблицы 4
Номер сечения |
|
|
|
|
|
|
|
|
|
|
14 |
4 |
2801,34 |
1,30088 |
1632,50 |
0,0001424 |
1028,88 |
1,58668 |
1,5154 |
224,566 |
1,13719 |
15 |
3 |
2715,3 |
1,53047 |
1786,29 |
0,0001675 |
1011,62 |
1,76578 |
1,6582 |
233,414 |
1,13752 |
16 |
2 |
2595,59 |
1,97464 |
1975,10 |
0,0002162 |
987,854 |
1,99938 |
1,8335 |
245,498 |
1,13826 |
17 |
1 |
2392,87 |
3,18156 |
2243,72 |
0,0003483 |
948,482 |
2,36559 |
2,0828 |
264,318 |
1,1404 |
18 |
0,5 |
2189,12 |
5,27377 |
2463,47 |
0,0005773 |
910,153 |
2,70666 |
2,2868 |
280,646 |
1,14385 |
19 |
0,25 |
1980,74 |
8,85472 |
2646,93 |
0,0009693 |
872,223 |
3,03469 |
2,4571 |
294,628 |
1,14897 |
20 - а |
0,1194 |
1754,55 |
15,4513 |
2810,60 |
0,0016915 |
828,072 |
3,39414 |
2,6091 |
307,201 |
1,15622 |
21 - ан |
0,048 |
1493,73 |
30,9025 |
2975,85 |
0,003383 |
767,902 |
3,87529 |
2,7625 |
320,014 |
1,16511 |
Распределение параметров потока по длине проточной части сопла рассчитано при помощи программного комплекса «Астра» [4]. Подробные результаты приведены в Приложении Б.
Теоретическое
значение коэффициента сопла
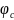 определяют по
формуле[7]:
определяют по
формуле[7]:
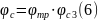
где
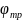 - коэффициент,
учитывающий потери в сопле на трение;
- коэффициент,
учитывающий потери в сопле на трение;
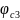 - коэффициент,
характеризующий потери из-за наличия
радиальной составляющей скорости на
выходе из сопла.
- коэффициент,
характеризующий потери из-за наличия
радиальной составляющей скорости на
выходе из сопла.
Разбиваем сопло на несколько участков по длине и для каждого определяем осевую составляющую силы трения по формуле[7]:
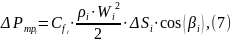
где
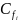 - коэффициент
трения на i-том
участке;
- коэффициент
трения на i-том
участке;
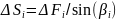 - боковая поверхность
участка;
- боковая поверхность
участка;
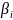 - угол наклона
контура к оси сопла;
- угол наклона
контура к оси сопла;
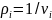 -
плотность продуктов сгорания;
-
плотность продуктов сгорания;
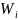 -
скорость продуктов сгорания;
-
скорость продуктов сгорания;
На данном участке все параметры и свойства рабочего тела принимаются постоянными, равными среднему арифметическому значению в расчетных сечениях, ограничивающих расчетный участок.
Коэффициент
трения
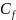 можно
определить по формуле [7]:
можно
определить по формуле [7]:
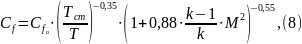
где
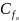 -
коэффициент трения для несжимаемой
жидкости (для технически гладких
поверхностей = 0,003)[7, стр. 21];
-
коэффициент трения для несжимаемой
жидкости (для технически гладких
поверхностей = 0,003)[7, стр. 21];
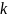 - показатель
адиабаты (усредним по соплу;
- показатель
адиабаты (усредним по соплу;
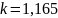 );
);
- число Маха;
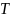 - температура
рабочего тела вне пограничного слоя;
- температура
рабочего тела вне пограничного слоя;
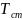 - температура
стенки (при
- температура
стенки (при
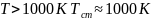 ,
,
при
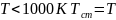 )[6];
)[6];
Суммарная сила
трения:
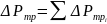
Коэффициент трения определим по формуле:
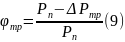
где
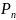 - пустотная тяга двигателя;
- пустотная тяга двигателя;
Результаты расчета представлены в таблицах 5,6.
Таблица 5. К расчету потерь на трение на дозвуковом участке сопла
Номер участка, i |
|
|
|
|
|
|
1 |
4,5 |
13,289 |
260,48 |
0,97323 |
0,527972 |
1,0424 |
2 |
4,466 |
12,522 |
471,72 |
0,89306 |
0,039797 |
0,2212 |
3 |
4,43 |
11,700 |
624,64 |
0,9409 |
0,021186 |
0,2015 |
4 |
4,39 |
10,870 |
753,94 |
0,97248 |
0,015664 |
0,2066 |
5 |
4,348 |
10,031 |
871,98 |
0,98955 |
0,013103 |
0,215 |
6 |
4,314 |
9,411 |
956,84 |
0,99654 |
0,006021 |
0,1115 |
7 |
4,289 |
8,984 |
1012,08 |
0,999 |
0,005822 |
0,1148 |
8 |
4,268 |
8,625 |
1058,39 |
0,99992 |
0,003936 |
0,0811 |
Таким
образом получаем на дозвуковом участке
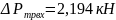
Таблица
6.
К
расчету потерь на трение на сверхзвуковом
участке сопла
(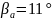 )
)
Номер участка, i |
|
|
|
|
|
9 |
4,242 |
8,18602 |
1113,2 |
0,000941 |
0,02 |
10 |
4,209 |
7,6874 |
1176,72 |
0,002006 |
0,044 |
11 |
4,18 |
7,24848 |
1232,25 |
0,003127 |
0,071 |
12 |
4,13 |
6,55893 |
1317,88 |
0,010146 |
0,234 |
13 |
4,068 |
5,79059 |
1420,12 |
0,01157 |
0,27 |
14 |
3,982 |
4,81823 |
1548,6 |
0,032437 |
0,732 |
15 |
3,863 |
3,76105 |
1709,39 |
0,045956 |
0,958 |
16 |
3,723 |
2,75393 |
1880,69 |
0,088908 |
1,582 |
17 |
3,508 |
1,65505 |
2109,41 |
0,241585 |
3,063 |
18 |
3,248 |
0,90756 |
2353,59 |
0,41879 |
3,356 |
19 |
2,997 |
0,5015 |
2555,2 |
0,716786 |
3,453 |
20 |
2,744 |
0,27323 |
2728,76 |
1,320415 |
3,617 |
21 |
2,455 |
0,13494 |
2893,22 |
3,092813 |
4,21 |
Зададимся рядом углов раскрытия конического сопла и рассчитаем соответствующие им значения . Результаты расчета представлены в таблице 8.
Коэффициент, учитывающий потери на рассеивание, вычисляется по формуле:
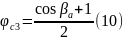
Найдем максимум
из произведений
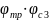 и по нему
определим оптимальный угол для конического
сопла.
и по нему
определим оптимальный угол для конического
сопла.
Пример расчета
для угла
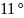 :
:
По данным таблицы 6 определим . Необходимые коэффициенты рассчитаем по формулам (6), (9), (10).
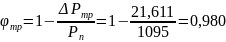
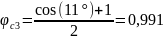
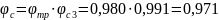
Таблица
8.
Оптимизация угла наклона
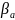 образующей
конического сопла
образующей
конического сопла
|
6° |
7° |
8° |
9° |
10° |
11° |
12° |
13° |
14° |
15° |
|
0,997 |
0,996 |
0,995 |
0,994 |
0,992 |
0,991 |
0,989 |
0,987 |
0,985 |
0,983 |
|
39,967 |
34,212 |
29,89 |
26,522 |
23,823 |
21,611 |
19,763 |
18,195 |
16,848 |
15,677 |
|
0,9635 |
0,9688 |
0,9727 |
0,9758 |
0,9782 |
0,9803 |
0,982 |
0,9834 |
0,9846 |
0,9857 |
|
0,96086 |
0,96515 |
0,96797 |
0,96977 |
0,97081 |
0,97126 |
0,97122 |
0,97078 |
0,96999 |
0,96889 |
По приведенной
методике расчета оптимальный угол
полураскрытия конического сопла
получается равным
,
что соответствует коэффициенту сопла