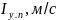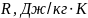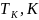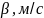3 Условная оптимизация соотношения компонентов по максимальному пустотному удельному импульсу
3.1 Расчёт стехиометрического соотношения компонентов
Окислитель[2]:
Азотная кислота
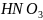– 70% (по массе)
Азотный тетраоксид
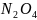– 27% (по массе)
Вода
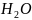– 3% (по массе)
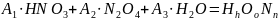
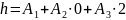
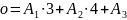
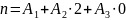
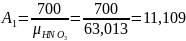
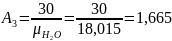
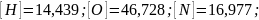
Удельная формула
окислителя:
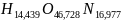
Полную энтальпию окислителя рассчитаем как сумму произведений полных энтальпий компонентов [2] на соответствующие массовые доли:
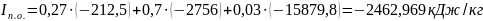
Горючее[3]:
НДМГ – 97,1% (по массе)
Примеси:
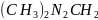– 1,8% (по массе)
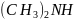– 1,1% (по массе)
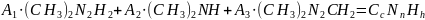
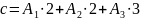
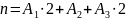
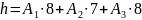
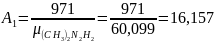
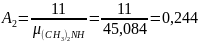
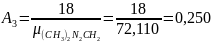
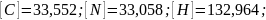
Удельная формула
горючего:
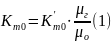
Массовое
стехиометрическое соотношение компонентов
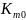можно получить из соотношения, вытекающего
из баланса валентностей окислительных
и горючих элементов. Т.к. рассматриваются
удельные формулы компонентов (т.е.
),
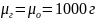то с учетом (1):
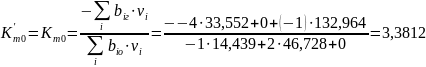
3.2 Подготовка данных, расчёт и построение графиков в зависимости от и при различных допущениях о равновесности процесса
Для нахождения оптимального соотношения компонентов зададим ряды коэффициентов избытка окислителя для различных предположений течения в сопле (дня равновесного, для частично замороженного, для химически замороженного).
Двигатель работает по схеме с дожиганием газогенераторного газа, поэтому повышения энтальпии не происходит. Полная энтальпия окислителя рассчитана в 3.1, полную энтальпию горючего примем согласно [3]. Файлы исходных данных для программного комплекса «Астра» формируются в следующем виде [4]:
для равновесного течения:
┌───────────────────────────── Исходные данные ──────────────────────────────┐
i=0,p=15,pa=kp,0.048,
ox=(h14.439o46.728n16.977[-2462.969]),
fuel=(c33.552n33.058h132.964[823.6]),
alpha=0.5,0.6,0.7,0.8,0.9,0.95,0.96,0.97,0.98,0.99,1.,1.01,1.02,1.03,1.1;
└────────────────────────────────────────────────────────────────────────────┘
для частично замороженного течения:
┌───────────────────────────── Исходные данные ──────────────────────────────┐
<FREX>
i=0,p=15,pa=kp,0.048,
ox=(h14.439o46.728n16.977[-2462.969]),
fuel=(c33.552n33.058h132.964[823.6]),
alpha=0.8,0.81,0.82,0.83,0.84,0.85,0.86,0.87,0.88,0.89,0.9;
└────────────────────────────────────────────────────────────────────────────┘
для полностью замороженного течения:
┌───────────────────────────── Исходные данные ──────────────────────────────┐
<FREX>
i=0,p=15,pa=0.048,
ox=(h14.439o46.728n16.977[-2462.969]),
fuel=(c33.552n33.058h132.964[823.6]),
alpha=0.8,0.81,0.82,0.83,0.84,0.85,0.86;
└────────────────────────────────────────────────────────────────────────────┘
Теперь получим действительное массовое соотношение компонентов для заданных коэффициентов избытка окислителя по формулам (2), (3), (4).
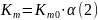
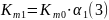
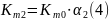
Полученные данные сводим в таблицы 1,2,3.
Таблица 1. Зависимость от и . Равновесное течение
|
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,95 |
0,96 |
0,97 |
|
1,690 |
2,029 |
2,367 |
2,705 |
3,043 |
3,212 |
3,246 |
3,280 |
|
2865,49 |
2957,13 |
3031,40 |
3085,65 |
3123,17 |
3135,11 |
3136,77 |
3138,10 |
|
442,46 |
408,32 |
381,91 |
361,96 |
347,82 |
342,53 |
341,59 |
340,68 |
|
2459,4 |
2775,6 |
3017,3 |
3172,8 |
3231 |
3229,4 |
3227,3 |
3224,6 |
|
1589,9 |
1634,2 |
1660,6 |
1672,0 |
1664,7 |
1653,9 |
1651,3 |
1648,6 |
|
0,98 |
0,99 |
1,00 |
1,01 |
1,02 |
1,03 |
1,1 |
|
|
3,313 |
3,347 |
3,381 |
3,415 |
3,449 |
3,482 |
3,719 |
|
|
3139,01 |
3139,34 |
3138,08 |
3129,35 |
3119,95 |
3110,40 |
3043,17 |
|
|
339,80 |
338,95 |
338,13 |
337,34 |
336,58 |
335,84 |
331,30 |
|
|
3221,5 |
3217,9 |
3213,8 |
3209,4 |
3204,6 |
3199,5 |
3155,8 |
|
|
1645,8 |
1642,9 |
1639,9 |
1636,9 |
1633,8 |
1630,6 |
1607,5 |
|
Таблица
2.
Зависимость
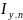от
и
.
Частично замороженное течение
|
0,5 |
0,6 |
0,7 |
0,82 |
0,83 |
0,84 |
0,85 |
|
1,69 |
2,029 |
2,367 |
2,772 |
2,806 |
2,84 |
2,874 |
|
2811,88 |
2926,17 |
3001,03 |
3042,61 |
3043,33 |
3043,59 |
3043,39 |
|
0,86 |
0,9 |
1 |
1,01 |
1,02 |
1,03 |
1,1 |
|
2,908 |
3,043 |
3,381 |
3,415 |
3,449 |
3,482 |
3,719 |
|
3042,72 |
3035,66 |
2994,27 |
2988,88 |
2983,33 |
2977,66 |
2935,03 |
Таблица 3. Зависимость от и . Полностью замороженное течение
|
0,5 |
0,6 |
0,7 |
0,8 |
0,81 |
0,82 |
0,83 |
|
1,69 |
2,029 |
2,367 |
2,705 |
2,739 |
2,772 |
2,806 |
|
2807,68 |
2917,65 |
2983,64 |
3008,58 |
3008,76 |
3008,51 |
3007,86 |
|
0,9 |
1 |
1,01 |
1,02 |
1,03 |
1,1 |
|
|
3,043 |
3,381 |
3,415 |
3,449 |
3,482 |
3,719 |
|
|
2993,08 |
2949,72 |
2944,5 |
2939,16 |
2933,73 |
2893,6 |
|
Построение графиков в зависимости от и от при различных допущениях о равновесности процесса.
Данные для построения графиков были рассчитаны в программном комплексе «Астра» [4].
Полная распечатка расчётов приведена в приложении А.
Графики пустотных удельных импульсов построены на втором листе проекта. По ним видно, что для каждого из рассматриваемых случаев течения имеется свой максимум:
для равновесного
течения
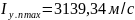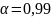при
и
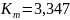
для частично
замороженного течения
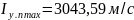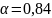при
и
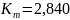
для полностью
замороженного течения
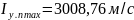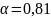при
и
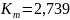
Вид
графиков
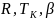подтверждают наличие максимума пустотного
удельного импульса (они построены только
для равновесного течения в сопле).