3.3 Анализ поведения функции в зоне максимума, минимума
и в центре факторного пространства
Данный подход позволяет оценить степень влияния факторов на изучаемую функцию и провести их ранжирование в каждой из рассматриваемых зон.
Рассмотрим квадратичное уравнение
Однофакторные модели
при различных уровнях стабилизации
остальных факторов сводим в таблицу 8.
Таблица 8 - Однофакторные модели
|
В зоне min
|
В зоне max
|
В центре факторного пространства
|
x1 |
|
|
|
x2 |
|
|
|
x3 |
|
|
|
Данные таблицы 8 являются основанием для настроения однофакторных зависимостей. График этих зависимостей в зоне max, min и в центре факторного пространства показаны на рисунке 3.
На графиках указаны числовые значения (перепад значений) для всех трех зон.
Ранжирование в зоне минимума дает ряд
,
т.е.
.
Ранжирование факторов в зоне максимума дает ряд
,
т.е.
.
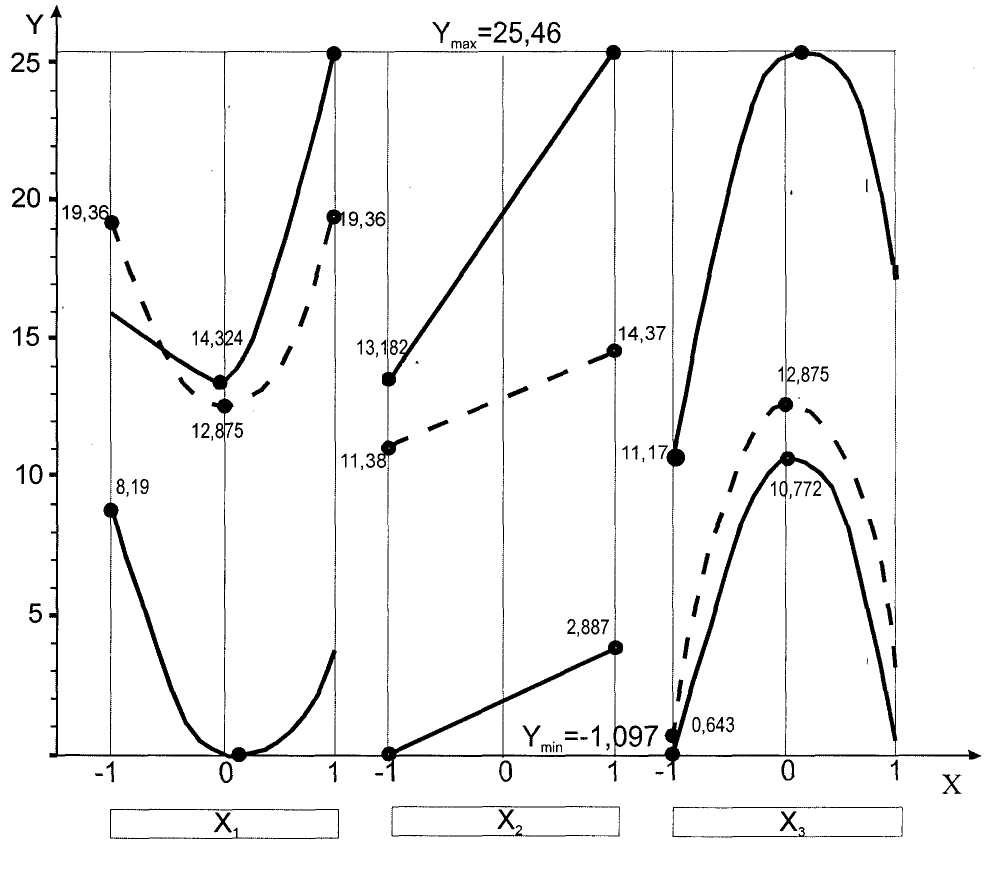
Рисунок 3 - Однофакторные зависимости
Ранжирование в центре факторного пространства дает ряд
,
т.е.
.
в зоне минимума наиболее сильно влияет x3, существенно влияет x1, наименьшее влияние оказывает фактор x2;
в зоне максимума наиболее сильно влияет x3, существенно влияет x2, наименьшее влияние оказывает фактор x1;
в центре факторного пространства наиболее сильно влияет x3, существенно влияет x1, наименьшее влияние оказывает фактор x2;
3.4 Оценка значимости коэффициентов модели при нарастающей степени риска
При данном анализе значимость коэффициентов регрессии проверяется многократно от = 0,001 до = 0,2 (таблица 9).
Таблица 9 - Критические значения коэффициентов модели (при k = 3)
|
0,001 |
0,005 |
0,01 |
0,02 |
0,05 |
0,1 |
0,2 |
t |
31,599 |
14,089 |
9,925 |
6,965 |
4,303 |
2,92 |
1,886 |
|
8,942 |
3,987 |
2,809 |
1,97 |
1,218 |
0,826 |
0,533 |
|
9,98 |
4,453 |
3,136 |
2,20 |
1,360 |
1,051 |
0,596 |
|
18,005 |
8,027 |
5,655 |
3,966 |
2,450 |
1,663 |
1,075 |
,
где t - численное значение критерия Стьюдента;
- среднеквадратическая ошибка в
определении коэффициента регрессии.
Заполнение таблицы 9 осуществляется следующим образом:
- для каждого из приложения 1 выписываются значения t;
- для каждой из групп взаимодействий определяется критическое значение ( biкр, bijкр и biiкр).
В таблицу 10 запишем все рассчитанные коэффициенты (в нашем примере это уравнение регрессии от 3-х факторов), определенные до исключения незначимых коэффициентов.
Таблица 10 - Начальные коэффициенты квадратичной модели
b1 |
b2 |
b3 |
b11 |
b22 |
b33 |
b12 |
b13 |
b23 |
b123 |
0,48 |
1,49 |
1,27 |
6,826 |
-1,424 |
-10,624 |
4,388 |
0,888 |
0,188 |
1,838 |
Используя таблицу 9 и таблицу 10 для каждого уровня значимости строим графы связи (рисунок 4).
Рисунок 4 - Изменение графов связи между 3-мя факторами
Анализ графов связи показывает, что с уменьшением вероятности появления ошибки, для приведенной модели наиболее сильным взаимодействием является , которое имеет место при = 0,005, т.е. достаточно высокой статистической надежности (99,5 %).