3. Анализ и интерпретация модели

1. Определение максимального и минимального значения исследуемой функции

Для поиска экстремальных x_i необходимо использовать таблицу в приложении В.

Алгоритм определения y_max рассмотрим на следующем примере. Допустим, что в результате расчетов было получено квадратичное уравнение вида

(3.1)

Распишем данное уравнение на систему квазиоднофакторных моделей

(3.2)

(3.3)

. (3.4)

Из системы квазиоднофакторных моделей (3.2, 3.3, 3.4) выбираются все модели, для которых b_ii  0.

В нашем случае это модели (3.2) и (3.3). Для этих моделей экстремальное значение может достигаться только на границах эксперимента, т.е. x_i = 1, однозначное значение x_i может быть получено, если выполняется условие

. (3.5)

При этом знак x_i определяет знак b_i.

Проверим условие (3.5) для модели (3.2)

,

условие не выполняется, следовательно возможны два конкурирующих решения x₁ = +1 и x₁ = -1.

Принимаем x₁ = +1, подставляем его в основное уравнение (3.1), приводим подобные и заново расписываем в виде системы моделей

(3.6)

. (3.7)

Для модели (3.6) b₂₂ = 0, проверяем условие (3.5) , условие выполнилось, следовательно, , т.к. коэффициент (+5.878) при x₂ положительный.

Приведем подобные

Для моделей, где b_ii < 0 положение находится внутри области эксперимента , если выполняется условие

(3.8)

В нашем случае для модели (3.7) b_ii < 0,

.

Так как условие (3.8) выполнилось, определим по зависимости (3.9)

(3.9)

.

В результате отработки одной ветви дерева поиска y_max получили один из альтернативных max.

при .

Рассмотрим вторую ветвь дерева поиска:

принимаем

приведем подобные

(3.10)

(3.11)

Для модели (3.10) , проверяем условие (3.5) , условие выполнилось, следовательно, , т.к. коэффициент (-2,898) при отрицательный.

Приводим подобные:

аналогично расчету приводимому в первой ветви

при .

Из двух альтернативных решений выбираем глобальный максимум исследуемой функции:

.

Для определения минимального значения смотри колонку minY в приложении 3

3.2 Построение двумерных сечений поверхности отклика

Двумерные сечения поверхности отклика строятся для двух факторов , при этом остальные факторы необходимо зафиксировать на постоянном уровне. Значение этого уровня зависит от постановки задачи, условий анализа изучаемой функции и т.д. При принятых постоянных значениях остальных факторов, не участвующих в построении графика, их значения подставляются в полученное уравнение регрессии, уравнение сокращается на порядок (n1) и получается зависимость от двух анализируемых факторов x_i и x_j.

Для построения графика функции необходимо иметь следующие параметры: для преобразованных функций, шаг изменения функции , а также просчитанные значения функции в четырех краевых точках графика . Значения функции в краевых точках позволяют определиться с диапазоном изменения функции для данного уравнения .

Шаг изменения функции при построении определяется из выражения

,

где n – количество сечений.

Двухфакторная модель второго порядка в зависимости от значений коэффициентов b_i, b_ii и b_ij может представлять собой одну из поверхностей второго порядка, представленных на рисунке 1.

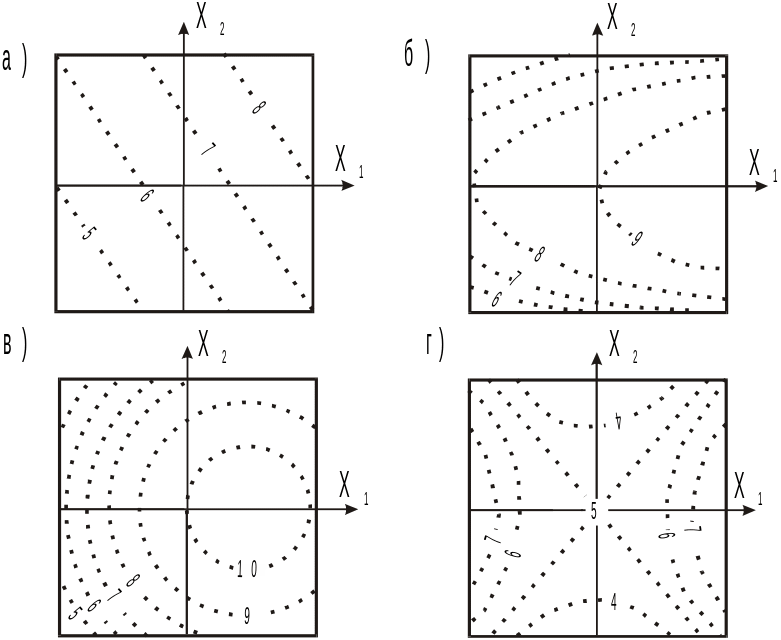
а - плоскость (b₁₁ = b₂₂ = b₁₂ = 0);

б - параболический цилиндр (b₁₁ = b₁₂ = 0);

в - эллиптический параболоид (b₁₁ > 0, b₂₂ > 0);

г - гиперболический параболоид (b₁₁ < 0, b₂₂ < 0).

Рисунок 1 - Примеры двумерных сечений поверхности отклика

На рисунке 2 приведен пример построения двумерного сечения поверхности отклика для

1,5

- область минимальных значений функции

- область максимальных значений функции

Расстояние между саженцами, м

2,0

4,0

6,0

0,5

2,5

, при

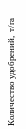
Рисунок 2 - Пример двумерного сечения поверхности отклика

Анализ двумерных сечений поверхностей отклика позволяет как качественно, так и количественно оценить поведение функции в пределах выбранного сечения факторного пространства. Для информативности помимо шкалы кодированных значений факторов, на рисунке 2 приведены диапазоны изменения факторов в натуральных единицах измерения. Это позволяет без перекодировки полученного уравнения регрессии, оперативно, без потери общности, проанализировать изучаемый процесс.