1 Построение линейной регрессионной модели

Для определения порядка модели (линейная модель или модель более высокого порядка), необходимо на первом этапе использовать исходную матрицу планирования (таблица 1)

Таблица 1 - Исходная матрица

1	2	3	4	5	6	7	8	9	10
1	+1	-1	+1	+1	-1	-1	+1	-1
2	+1	-1	-1	+1	+1	-1	-1	+1
3	+1	+1	-1	+1	-1	+1	-1	-1
4	+1	+1	+1	+1	+1	+1	+1	+1
5	+1	+1	+1	-1	+1	-1	-1	-1
6	+1	-1	+1	-1	-1	+1	-1	+1
7	+1	-1	-1	-1	+1	+1	+1	-1
8	+1	+1	-1	-1	-1	-1	+1	+1

Суммы , и другие получаются путем умножения вектора-столбца на каждый вектор-столбец _.

Расчет коэффициентов линейной модели выполняется по общей формуле (1)

, (1)

где - сумма для каждого из взаимодействий таблицы 1;

- количество опытов в исходной матрице планирования.

.

Для дальнейшего анализа модели необходимо определить критические значения коэффициентов модели по формуле (2)

, (2)

где t - численное значение критерия Стьюдента, определяется по таблице (приложение 1) для заданного уровня значимости ( = 0,05);

S_э - среднеквадратическая ошибка эксперимента;

- Количество опытов в исходной матрице;

- ошибка определения коэффициентов .

Коэффициент уравнения регрессии считается значимым, если выполняется условие

.

Определение значимости коэффициентов модели сводится в таблицу 2.

Таблица 2  Определение значимости коэффициентов

Параметры	Коэффициенты
Значимые

В результате получаем окончательный вид уравнения регрессии, включающего значимые коэффициенты:

.

Для определения адекватности полученного уравнения находим дисперсию неадекватности по формуле:

,

где - число опытов в матрице;

- количество значимых коэффициентов;

- число степеней свободы при определении дисперсии неадекватности.

Расчет дисперсии неадекватности сводим в таблицу 3.

Модель считается адекватной, если выполняется условие:

где 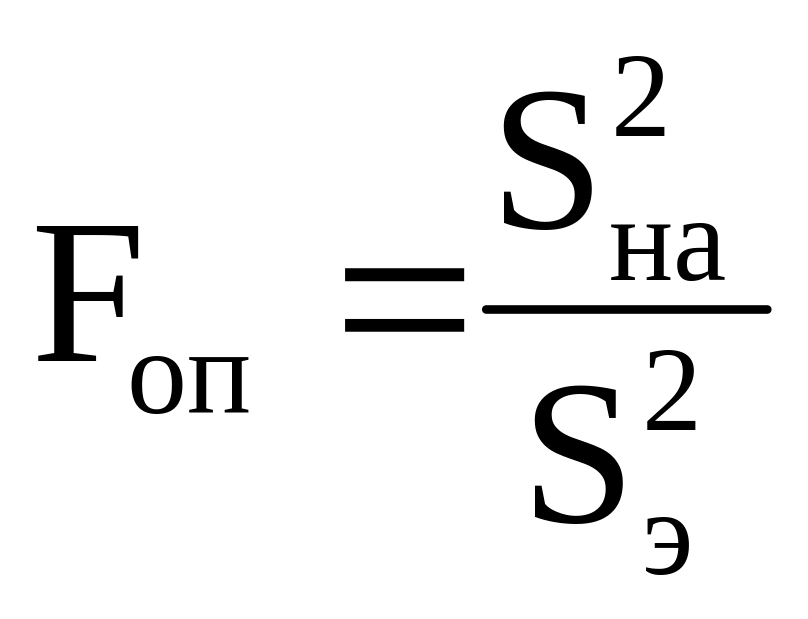- опытное значение критерия Фишера;

- дисперсия неадекватности;

- дисперсия эксперимента;

- теоретическое значение критерия Фишера, определяется по статистическим таблицам (приложение Б).

Таблица 3 – Расчет дисперсии неадекватности

				% ошибки
1
2
3
4
5
6
7
8

Процент ошибки вычисляется по формуле:

Для определения необходимо иметь три параметра:

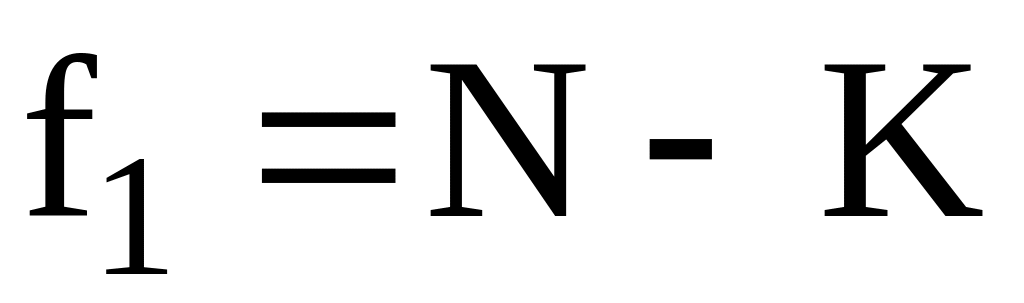1. - число степеней свободы при определении

дисперсии неадекватности;

2) - число степеней свободы при определении

дисперсии эксперимента ;

- число опытов при определении дисперсии эксперимента.

3) = 0,05 - уровень значимости.

Если линейная модель неадекватна, т.е. , необходимо ее достроить до квадратичной модели и продолжить анализ и интерпретацию полученных результатов.

Если модель адекватна, т.е. , необходимо проанализировать % ошибки (см. табл. 3). В случае, если % хотя бы в одном из опытов превышает 5%, то использовать данную модель для дальнейшего анализа выходной функции и на практике нельзя. В этом случае так же необходимо произвести расчет модели в квадратичной области, либо уточнить исходные данные, путем повтора отдельных опытов.