- •Ведение
- •1. Множества и операции над ними.
- •1.1. Основные понятия о множествах.
- •1.2. Операции над множествами.
- •Упражнения.
- •2. Логика высказываний
- •2.1. Понятие высказывания
- •2.2. Логические операции над высказываниями.
- •2.3. Сложные высказывания.
- •Упражнения.
- •3. Логика предикатов.
- •3.1. Понятие предиката.
- •3.2. Логические операции над предикатами.
- •3.3. Кванторные операции.
- •Упражнения.
- •4. Приложение математической логики.
- •4.1. Виды теорем и их взаимосвязь.
- •4.2. Необходимое и достаточное условия.
- •4.3. Метод математической индукции.
- •4.4. Теорема дедукции.
- •4.5. Приложение логики высказываний к релейно-контактным схемам.
- •Упражнения.
- •Ответы и указания к решениям.
- •Глава 1.
- •Глава 2.
- •Глава 3.
- •Глава 4.
- •Заключение
- •Список литературы
2.3. Сложные высказывания.
Введённые пять логических операций дают возможность, исходя из первоначального набора элементарных высказываний, построить некоторое количество сложных высказываний. Истинность или ложность сложного высказывания в зависимости от истинности или ложности составляющих его высказываний можно установить, построив таблицу истинности сложного высказывания, последовательно используя таблицы истинности логических операций.
Пример.
Составить таблицу истинности для
высказывания
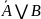 .
.
Истина и ложь могут распределяться между двумя высказываниями четырьмя различными способами, следовательно, таблица истинности состоит из четырёх строк:
-
А
В
1
1
0
1
1
0
0
0
0
1
1
1
0
0
1
1
Третий столбец заполняется по первому на основании таблицы истинности для отрицания, последний – по второму и третьему, с использованием таблицы истинности для дизъюнкции.
Сравнивая полученную таблицу истинности для высказывания с таблицей истинности для импликации , видно, что высказывания и имеют одинаковые таблицы истинности. Такие высказывания называются равносильными. Равносильные высказывания принято соединять знаком равенства: = .
Употребление знака равенства для соединения равносильных высказываний совершенно естественно.
Действительно, сложные высказывания и имеют различную форму: из элементарных высказываний А и В они строятся с помощью различных логичных операций. Но для логики высказываний существенно только одно: будет ли при определённом распределении значений истины и лжи для элементарных высказываний составленное из них сложное высказывание истинным или ложным. В этом смысле высказывания и «одинаковы»: если высказываниям А и В приписаны какие-т значения истины или лжи, то высказывания и будут либо оба истинны, либо оба ложны.
Пример. Составить таблицу истинности для высказывания
 .
.
Истина и ложь могут распределяться между двумя высказываниями четырьмя различными способами, следовательно, таблица истинности состоит из четырёх строк:
А |
В |
|
|
|
|
|
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
Третий столбец заполняется по первым двум на основании таблицы истинности для импликации, четвёртый и пятый – по второму и первому столбцу на основании таблицы истинности для отрицания. Шестой столбец составляется по четвертому и пятому с помощью таблицы истинности для импликации, и, наконец, последний седьмой столбец выписывается по третьему и шестому согласно таблице истинности для эквиваленции.
Из таблицы видно, что высказывание истинно всегда, т.е. при любом наборе значений истины и лжи для составляющих его высказываний А и В. Такие высказывания называются тождественно истинными или тавтологией и обозначаются латинской буквой I. Поэтому для приведённого в примере высказывания можно записть:
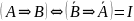 .
.
Наряду с тождественно истинными высказывания рассматриваются тождественно ложные, т.е. ложные всегда, независимо от того, истины или ложны составляющие их высказывания. Тождественно ложные высказывания обозначаются латинской буквой L.
Тождественно
истинные и тождественно ложные
высказывания играют большую роль в
процессе логических заключений. Иногда
их называют законами логики. Например,
легко проверяемое равенство
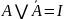 выражает так называемый закон исключения
третьего: всякое высказывание либо
истинно, либо ложно, третьего не дано.
Тождественно ложное высказывание
выражает так называемый закон исключения
третьего: всякое высказывание либо
истинно, либо ложно, третьего не дано.
Тождественно ложное высказывание
 выражает закон противоречия, согласно
которому никакое высказывание не может
быть одновременно истинным и ложным.
Равносильность
выражает закон противоречия, согласно
которому никакое высказывание не может
быть одновременно истинным и ложным.
Равносильность
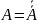 ( или
( или
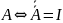 )
выражает закон отрицания отрицания.
Этот закон утверждает, что отрицание
отрицания совпадает с исходным
высказыванием.
)
выражает закон отрицания отрицания.
Этот закон утверждает, что отрицание
отрицания совпадает с исходным
высказыванием.
Приведем основные законы логики высказываний:
1. Коммутативность дизъюнкции
 .
.
2. Коммутативность конъюнкции
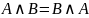 .
.
3. Ассоциативность дизъюнкции
 .
.
4. Ассоциативность конъюнкции
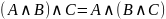 .
.
5. Законы дистрибутивности
 ,
,
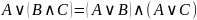 .
.
6. Законы де Моргана
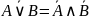 ,
,
 .
.
7. Законы идемпотентности
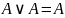 ,
,
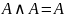 .
.
8. Законы, включающие тождественно истинные (I) и тождественно ложные (L) высказывания
 ,
,
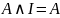 ,
,
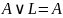 ,
,
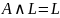 .
.
9. Закон замены операции импликации
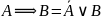 .
.
10. Законы замены операции эквивалентности
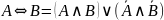 ,
,
 ,
,
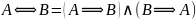 .
.
Пример 1. Доказать равносильность:
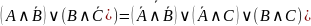 .
.
Используя законы де Моргана, можно записать
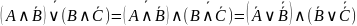 .
.
В
силу закона отрицания отрицания,
полученное высказывание равносильно
следующему
 .
.
Теперь, используя закон дистрибутивности и ассоциативности дизъюнкции, можно преобразовать полученное выражение

Согласно
закону противоречия, выражение
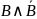 является тождественно ложным,
является тождественно ложным,
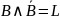 .
.
Применение закона 10, даёт доказательство равносильности
.
Пример 2. Упростить высказывание

Так
как
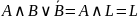 ,
,
,
,
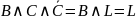 ,
то предложенное высказывание равносильно
дизъюнкции ложных высказываний, т. е.
является тождественно ложным
,
то предложенное высказывание равносильно
дизъюнкции ложных высказываний, т. е.
является тождественно ложным
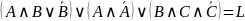 .
.