
- •Ведение
- •1. Множества и операции над ними.
- •1.1. Основные понятия о множествах.
- •1.2. Операции над множествами.
- •Упражнения.
- •2. Логика высказываний
- •2.1. Понятие высказывания
- •2.2. Логические операции над высказываниями.
- •2.3. Сложные высказывания.
- •Упражнения.
- •3. Логика предикатов.
- •3.1. Понятие предиката.
- •3.2. Логические операции над предикатами.
- •3.3. Кванторные операции.
- •Упражнения.
- •4. Приложение математической логики.
- •4.1. Виды теорем и их взаимосвязь.
- •4.2. Необходимое и достаточное условия.
- •4.3. Метод математической индукции.
- •4.4. Теорема дедукции.
- •4.5. Приложение логики высказываний к релейно-контактным схемам.
- •Упражнения.
- •Ответы и указания к решениям.
- •Глава 1.
- •Глава 2.
- •Глава 3.
- •Глава 4.
- •Заключение
- •Список литературы
Упражнения.
№ 1. Доказать основные свойства отношения включения:
Х X;
(XY) ( Y X) X=Y;
(XY) ( Y Z) XZ.
№ 2. Доказать следующие свойства пустого множества:
X; Х Х=, где Х – произвольное множество.
№ 3. Показать, что для любого натурального n имеет место эквивалентность:
Х1Х2 . . . XnX1X1=X2= . . . =Хn.
№ 4. Пусть k и n — натуральные числа и kn. Сколько различных подмножеств из k элементов содержит множество из n элементов? Сколько различных подмножеств содержит множество из n элементов?
№ 5. Используя результаты предыдущей задачи решить следующие:
1. Пусть М — некоторое множество n точек пространства. Сколько можно построить ломаных линий, вершинами которых являются какие-либо k точек из М и только точки из М?
2. Сколько всего ломаных линий, верщины которых суть точки множества М?
№ 6. Опишите каждое из следующих множеств, используя подходящее свойство:
а) {0, 1, 2, 3, 4, 5, 6, 1, 8, 9, 10};
б) {3, 6, 9, 12, 15};
в) {4, 9, 16, 25};
г) {10, 12, 14, 16}
№ 7. Пусть R— числовая прямая; изобразить на ней следующие множества:
а) 3<x<4;
б) х2—5х+6<0;
в) |х|<2.
№ 8. Доказать следующие формулы, выражающие отношение включения через операции объединения и пересечения.
а) XYXY=Y;
б) XYXY=X.
№ 9. Доказать следующие свойства пустого множества:
а) X=X;
б) Х = .
№ 10. Найти:
а) {а, b, с}{а, с, d, f };
б) {а, b, с}{b, с};
в) {а, b, с, d)\{a, f, g, k}
Обозначенные различными буквами элементы различны.
№ 11. Пусть N1 = { 1, 3,7}; N2 = { 0, 1, 3, 4, 8 } . Из каких элементов состоят множества:
а) N1N2 и N2 N1;
б) (N1N2) ( N2 N1) и ( N2 N1) (N1N2);
№ 12.
Пусть даны множества А, В, С и
 ,
,
 ,
,
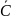 - дополнения соответствующих множеств
А, В, С до универсального множества U.
Изобразите при помощи кругов Эйлера
следующие множества (АВ
С=):
- дополнения соответствующих множеств
А, В, С до универсального множества U.
Изобразите при помощи кругов Эйлера
следующие множества (АВ
С=):
а)
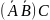 ;
;
б)
 ;
;
в)
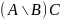 ;
;
г)
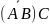 ;
;
д)
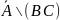 ;
;
е)
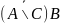 ;
;
ж)
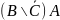 ;
;
з)
 ;
;
и)
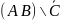 ;
;
к)
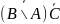 ;
;
л)
 ;
;
м) ;
№ 13. Используя круги Эйлера, докажите следующие равенства:
а)
 ;
;
б) ;
в)
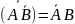 ;
;
г)
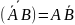 ;
;
д)
 ;
;
е)
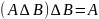 ;
;
ж)
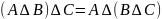 ;
;
з)
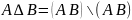 ;
;
и)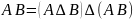 ;
;
к)
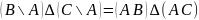 .
.
2. Логика высказываний
2.1. Понятие высказывания
Основным (неопределяемым) понятием математической логики является понятие «простого высказывания».
Под высказыванием обычно понимают всякое повествовательное предложение, утверждающее что-либо о чем-либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях места и времени. Логическими значениями высказываний являются «истина» и «ложь». Примерами высказываний являются следующие предложения:
Новгород стоит на Волхове.
Париж – столица Англии.
Карась не рыба.
Число 6 делится на 2 и на 3.
Если юноша окончил среднюю школу, то он получает аттестат.
Высказывания 1), 4), 5) истинны, а 2) и 3) – ложны.
Не всякое предложение является высказыванием. Так, к высказываниям не относятся вопросительные и восклицательные предложения, поскольку говорить об их истинности или ложности нет смысла. Не являются высказываниями и такие предложения: «Каша — вкусное блюдо», «Математика — интересный предмет»; нет и не может быть единого мнения о том, истинны эти предложения или ложны. Предложение «Существуют инопланетные цивилизации» следует считать высказыванием, так как объективно оно либо истинное, либо ложное, хотя никто пока не знает, какое именно. Предложения «Шел снег», «Площадь комнаты равна 20 м2», а2 =4 не являются высказываниями; для того чтобы имело смысл говорить об их истинности или ложности, нужны дополнительные сведения: когда и где шел снег, о какой конкретной комнате идет речь, какое число обозначено буквой а.
Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным. Примерами элементарных высказываний могут служить высказывания 1) и 2).
Изучением высказываний занимается специальная математическая дисциплина – математическая логика, точнее, тот раздел этой науки, который называется логикой высказываний.
Логика высказываний не занимается обоснованием того, почему тому или иному элементарному высказыванию приписано значение истины, а не лжи или, наоборот, лжи, а не истины.
