4.3. Метод математической индукции.

Во многих разделах арифметики, алгебры, геометрии, анализа приходится доказывать истинность предложений типа

(n) А(n),

т.е. предложения, выражающие некоторое свойство А, присущее любому натуральному числу n.

Доказательство истинности предложения А(n) для всех значений переменной часто удается провести методом математической индукции, который основан на следующем принципе:

Предложение А(n) считается истинным для всех натуральных значений переменной, если выполнены следующие два условия:

1. Предложение А(n) истинно для n=1.

2. Из предположения, что А(n) истинно для n=k (где k – любое натуральное число), следует, что оно истинно и для следующего значения n=k+1.

Этот принцип называется принципом математической индукции. Обычно он выбирается в качестве одной из аксиом, определяющих натуральный ряд чисел, и, следовательно, принимается без доказательства.

Под методом математической индукции понимают следующий способ доказательства. Если требуется доказать истинность предложения А(n) для всех натуральных n, то, во-первых, следует проверить истинность высказывания А(1) и, во-вторых, предположив истинность высказывания А(k), попытаться доказать, что высказывание А(k+1) истинно. Если это удается доказать, причем доказательство остается справедливым для каждого натурального значения k, то в соответствии с принципом математической индукции предложение А(n) признается истинным для всех значений n.

Метод математической индукции широко применяется при доказательстве теорем, тождеств, неравенств, при решении задач на делимость, при решении некоторых геометрических и многих других задач.

Пример:

  .

Доказательство. 

Проверим, работает ли эта формула при n = 1:

.

Предположим, что тождество верно при n = k, то есть

Проверим это тождество при n = k +1, то есть нужно доказать, что

.

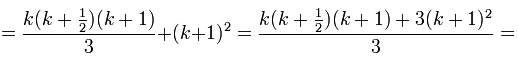
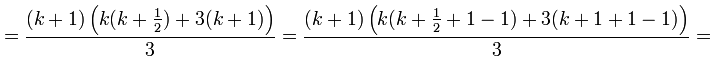
4.4. Теорема дедукции.

Дедукция (от лат. deductio - выведение), переход от общего к частному. Дедукция - это процесс логического вывода перехода по тем или иным правилам логики от некоторых данных предложений - посылок к их следствиям, причём в некотором смысле следствия всегда можно характеризовать как «частные случаи» общих посылок. Термин «Дедукция» употребляется так же и для обозначения конкретных выводов следствий из посылок, т. е. как синоним термина «вывод» в одном из его значений. И чаще как родовое наименование общей теории построений правильных выводов (умозаключений).

Изучение дедукции составляет одну из главных задач логики. В формальной логике, то как к самой по себе системе логических правил, так и к любым их применениям в любой области в полной мере относится положение о том, что всё, что заключено в любой полученной посредством дедуктивного умозаключения «логической истине», содержится уже в посылках, из которых она выведена: каждое применение правила в том и состоит, что общее положение относится к некоторой конкретной («частной») ситуации. Некоторые правила логического вывода подпадают под такую характеристику и совсем явным образом. Например, различные модификации так называемого правила подстановки гласят, что свойство доказуемости (или выводимости из данной системы посылок) сохраняется при любой замене элементов произвольной формулы данной формальной теории «конкретными» выражениями «того же вида».

Под дедукцией часто понимают и сам процесс логического следования. Это обусловливает тесную связь, а иногда даже отождествление, понятия «дедукция» с понятиями вывода и следствия, находящую своё отражение и в логической терминологии. Так, «Теоремой дедукции» принято называть одно из важных соотношений между логической связкой импликации, формализующей словесный оборот «Если..., то... » и отношением логического следования (выводимости): если из посылки А выводится следствие В, то импликация А  В («Если А..., то В...») доказуема т. е. выводима уже без всяких посылок, из одних только аксиом.