Упражнения.

№ 1. Какие из следующих выражений являются предикатами:

а) х делится на три (х пробегает множество натуральных чисел);

б) у = х² (х пробегает множество действительных чисел);

в) х² + х + 1 = 0 (х пробегает множество действительных чисел);

г) x²+2x+1 (х пробегает множество действительных чисел);

д) х есть мать у (х и у пробегают множество всех людей);

е) х и у (х и у пробегают множество всех людей).

№2. Пусть х, у, z пробегают множество действительных чисел. От какого числа переменных зависят следующие предикаты:

а) х² + у² = z²;

б) для всякого х найдется такой у, что х + у = 1;

в) существует z, такое, что для всякого х имеет место неравенство

х + у<z.

№3. Даны два предиката: Ф₁( х): х есть собака;

Ф₂(х): х обладает хорошим обонянием (х пробегает мно­жество всех живых существ).

Прочесть символическое выражение (х)( Ф₁(х) Ф₂(х))

№4. В следующих высказываниях выделить входящие в них предикаты и записать эти высказывания с помощью символики исчисления предикатов:

а) снег белый;

б) я живу в городе Саратове;

в) 2<3;

г) 2·2 = 4;

д) некоторые змеи ядовиты.

№5. Предикаты P₁ и Р₂ заданы на N высказывательными фор­мами «х — простое число» и «х — четное число». Найдите множест­во истинности предиката Р, заданного конъюнкцией этих высказы­вательных форм.

№6. Задайте множество значений переменной так, чтобы на этом множестве данные высказывательные формы были равносильны: а) «х кратно 3»; «х кратно 5»; б) «у — четное число»; «у — простое число»; в) x³—1 = 0; х²+2х-3=0; г) «z —ромб»; «диагонали в z взаимно перпендикулярны».

№7. Определите, равносильны ли на множестве М следующие высказывательные формы: а) 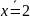, х≠2, М=R; б) , х2; М=R; в) 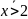, х<2; М=R; г) , х2; М=R; д) «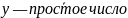 »,«у— составное число»; M=N; е) « », «у — нечетное число»; M=N;

ж) «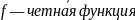 », « — нечетная функция»; М — множество всевозможных числовых функций число­вого аргумента; з) х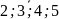{ }, х{1; 6; 7}; М={1; 2; 3; 4; 5; 6; 7}.

№8. Следующие высказывательные формы замените равносиль­ными им дизъюнкциями:

а) |х + 3| > 3; б) (х — 5)/(х— 1) > 0; в) х² — 5х + 6 = 0;

г) х² + у²≠ 0.

№9 Как записать символически равносильность двух уравнений

f₁ (х, у) = 0 и f₂ (x, у) = 0?

№10. Записать с помощью логической символики, что си­стема уравнений: f₁(х, у) = 0 и f₂ (x, у) = 0 несовместна (не имеет решений).

№11. Записать с помощью логической символики высказывания:

а) существует точно одно х, такое, что Ф(х);

б) существует по крайней мере два х, таких, что Ф(х);

в) существует не более двух х, таких, что Ф(х).

№12. Записать с помощью логической символики высказывания:

1. Для всех х, удовлетворяющих условию Ф₁ (x), имеет ме­сто Ф₂ (х).

2. Существует х, удовлетворяющий условию Ф₁ (x)и та­кой, что имеет место Ф₂(х) .

№13. Определите, следует ли одна высказывательная форма из другой, если M=R:

а) |х]<3; х²—Зх+2=0; б) х⁴=16; х²=-2; в) х²+х-6=0; (х— 1)(х—2)(х—3) = 0; г) х—1>0; (х—2) (х—5) =0; д) sinx=2; х² + 5=0; е) х²+5х—6>0; х+1 = 1+х.

4. Приложение математической логики.

4.1. Виды теорем и их взаимосвязь.

1. Понятие теоремы.

Рассмотрим с точки зрения введённых во второй и третьей главах понятие теоремы. Большинство теорем, встречающихся в школьном курсе математики, представляют собой высказывания в виде

х А(х)В(х), хU. (1)

Ограничимся строением таких теорем. Возьмём, например, теорему: «Во всяком треугольнике против равных сторон лежат равные углы». Здесь на самом деле рассматриваются два предиката

А(Δ)={в ΔАВС стороны АВ и ВС равны}и В(Δ)={в ΔАВС угол А равен углу С}, заданных на множестве всех треугольников.

Теорема утверждает, что для любого треугольника из истинности А(Δ) следует истинность В(Δ), а это как раз можно записать кратко  Δ А(Δ)В(Δ) .

В формулировке каждой теоремы, имеющей структуру (1), будем различать:

1.Условие теоремы – предикат А(х).

2.Заключение теоремы – предикат В(х).

3. Разъяснительную часть теоремы – описание элементов множества U, на котором заданы предикаты А(х) и В(х) вместе с указанием на то, что импликации А(х)В(х) истинна для всех его элементов.

Нередко при формулировке теорем опускается разъяснительная часть. Например, теорема о диагоналях ромба формулируется так: «Диагонали ромба взаимно перпендикулярны». При этом, конечно, подразумевается, что утверждение теоремы относится к каждому ромбу. Из-за краткости формулировки теоремы о диагоналях ромба может показаться, что эта теорема не имеет формы (1). На самом деле это не так. Точная формулировка этой теоремы такова (напомним, что ромбом называется параллелограмм, у которого все стороны равны):

Пусть Р – множество параллелограммов и пусть А(р)={Параллелограмм р – ромб} и В(р)={диагонали параллелограмма р взаимно перпендикулярны} – два предиката, заданных на множестве Р. Тогда р А(р)В(р), т.е. для любого параллелограмма верно утверждение, если он – ромб, то его диагонали взаимно перпендикулярны.

2. Обратные теоремы.

Для всякой теоремы вида «если А, то В» можно сформулировать обратное ей пред­ложение «если В, то А». Однако не для всякой теоремы предложение, ей обратное, также является теоремой. Пусть, например, даны такие две теоремы: «Если два квадрата равны, то их площади равны»; «Если два прямоугольника равны, то их площади равны». Предложение «Если площади двух квадратов равны, то эти квадраты равны», обратное первой из данных теорем, является теоремой. Предложение «Если площади двух прямоугольников равны, то они равны», обратное второй из данных теорем, тео­ремой не является.

Эти примеры свидетельствуют о неравносильности предложений вида А(х)В(х) и В(х)А(х). В неравносильности предложений такого вида можно также убедиться, срав­нив таблицы истинности формул АВ и ВА:

А	В	АВ	ВА
и	и	и	и
и	л	л	и
л	и	и	л
л	л	и	и

Поскольку два последних столбца в таблице не оди­наковы, эквиваленция этих формул не является тавто­логией, т. е. они не равносильны. Более того, из таблицы видно, что одновременно с истинностью предложения ви­да «если А, то В», предложение вида «если В, то А» мо­жет быть как истинным, так и ложным.

Таким образом, если доказана истинность какого-ли­бо предложения, то независимо от этого обратное ему предложение требует доказательства или опровержения.

3. Противоположные теоремы.

Для всякой тео­ремы, сформулированной в виде импликации АВ, мож­но составить противоположное предложение . Пред­ложение, противоположное данной теореме, может быть также теоремой, но может ею и не быть. В этом легко убедиться, сравнив таблицы истинности формул АВ и ; в том случае, когда предложение вида АВ истинно, предложение . мо­жет быть как истинным, так и ложным. Следовательно, предложение, противоположное доказанной теореме, в свою очередь нуждается в доказательстве или опро­вержении.

Если условие или заключение данной теоремы пред­ставляет собой конъюнкцию или дизъюнкцию, то при со­ставлении предложения, противоположного этой теоре­ме, нужно учитывать соответствующий закон де Моргана . Иногда конъюнкция или дизъюнкция в формулировке теоремы присутствует не­явно, «замаскировано». Поэтому, чтобы правильно сформулировать предложение, противоположное данной теореме, нужно сначала тщательно проанализировать ее формулировку и выявить подразумеваемые конъюнкции или дизъюнкции (если таковые имеются). Например, в заключении теоремы «Если треугольник ABC равно­бедренный, то два его угла равны» скрыта дизъ­юнкция: A=B, или B=C, или A=C. От­рицание этой дизъюнкции дает конъюнкцию A≠B, или B≠C, или A≠C, что короче можно выразить так: «Никакие два угла треугольника ABC не равны».

4. Закон контрапозиции.

Нам осталось рассмотреть соотношение между обратно-противоположными предложениями, т. е. предложениями вида АВ и . Имеет место следующая равносильность :

АВ = - закон контрапозиции.

Согласно закону контрапозиции: 1) два предложения вида АВ и одновременно истинны, либо одновре­менно ложны; 2) предложение, обратно противополож­ное какой-либо теореме, также является теоремой; 3) вместо данной теоремы можно доказывать обратно-противоположную ей теорему.

Пусть, например, требуется доказать утверждение «Если m² нечетно, то m нечетно». Сформулируем и до­кажем обратно-противоположную теорему: «Если m чет­но, то m² четно»; действительно, если m четно, то m=2р {р — натуральное число), откуда m²=4р²=2·(2р²) =2q, т. е. m² четно. Предположение, обратно-противопо­ложное данному, доказано; следовательно, доказано и данное утверждение.

Если в равносильность АВ = подставить В вместо А и А вместо В, то получим ВА= . Из этой равносильности следует, что: 1) предложение, обратное данному, и предложение, противоположное данному, од­новременно истинны либо одновременно ложны; 2) из двух предложений — обратного данной теореме и ей про­тивоположного— достаточно доказать или опровергнуть какое-нибудь одно; тем самым будет доказано или соот­ветственно опровергнуто и второе.