Лекция 1. Матрицы и действия над ними.
1. Основные понятия и определения.
Матрицы впервые появились в середине 19-го века в работах английских математиков У. Гамильтона (1809-1865) и А.Кэли (1821-1895).
Примечание: Уильям Гамильтон – ирландский математик, иностранный член – корреспондент Петербургской Академии Наук (1837);
Артур Кэли (Кейли) – английский математик, иностранный член – корреспондент Петербургской Академии Наук (1870).
В настоящее время матрицы широко используются в прикладной математике, в частности, представляют собой удобный аппарат для компактной записи и последующего исследования и решения систем линейных уравнений.
Матрицей
типа (размера)
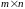называют прямоугольную числовую таблицу,
состоящую из
чисел, которые расположены в m
строках и n
столбцах.
Числа,
из которых составлена матрица, называются
элементами матрицы. Их обозначают
строчными буквами с двумя индексами,
например,
, где i-
номер строки (
),
j-
номер столбца (
),
в которых расположен этот элемент.
Матрицы обозначают
Иногда используют обозначение матриц:
Соответственно
элементы матрицы обозначаются
,
где i-
номер строки; j-
номер столбца.
Сокращенные обозначения:
Используется
также обозначение
.
Матрицу
как единый объект обозначают прописной
буквой А, В и т.д. При необходимости
указать тип (размер) матрицы используют
обозначения
Используется также обозначение
или
Набор
называется i-й
строкой матрицы
А, набор
называется j- м столбцом матрицы А.
Рядом матрицы называется строка или столбец.
Элемент
матрицы, стоящий в i-той
строке и j-
том столбце может также обозначаться
.
Чаще обозначается
.
Элементами матрицы могут быть не только действительные числа, но и комплексные, и даже другие математические объекты: функции, многочлены, матрицы, например:
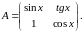
Мы
будем рассматривать только числовые
матрицы, т.е. матрицы, составленные из
действительных чисел. Множество всех
числовых матриц типа m×n
, элементами которых являются действительные
числа, обозначаются
.
Здесь
- обозначение множества действительных
чисел (
-
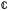множество комплексных чисел).
Если
матрица имеет тип 1×n,
т.е. у матрицы всего одна строка
,
то матрицу называют матрицей
- строкой.
Индекс строки можно опустить
.
Число элементов в матрице- строке
называют ее длиной:
n-
длина матрицы- строки.
Если матрица имеет тип m×1, т.е. у матрицы один столбец
,
то ее называют матрицей- столбцом. Число элементов в матрице- столбце называют ее высотой. Индекс столбца можно опустить
.
Матрицу-
строку и матрицу- столбец можно обозначать
и
.
Матрица, содержащая один столбец или одну строку, называется вектором (вектор-строка или вектор – столбец соответственно).
Матрица размера 1×1, состоящая из одного числа отождествляется с этим числом, т.е. (5)1×1 есть 5.
Иногда бывает удобно записывать матрицу как столбец из строк или как строку из столбцов.
Пусть
векторы - столбцы матрицы А.
Пусть
векторы - строки матрицы А.
Тогда матрицу А можно записать в виде столбца из строк
,
или в виде строки из столбцов
.
Подматрицей матрицы А размера m×n называется матрица A' размера r×s, составленная из элементов матрицы А, находящихся на пересечении выбранных r строк и s столбцов. Номера выбранных строк и столбцов должны следовать в порядке возрастания.
Пример 1.
(строк r=3, столбцов s=4), подматрица матрицы А будет иметь вид
.
Пример 2.
.
Подматрица, состоящая из трех строк и двух столбцов, в данном случае имеет вид
.
Квадратной матрицей порядка n называется матрица, которая имеет столько же столбцов, сколько и строк m=n
Порядок – это число строк (столбцов) квадратной матрицы.
При m≠n – матрица прямоугольная.
Последовательность
элементов
квадратных матриц называется главной
диагональю.
Элементы главной диагонали называются
диагональными.
Последовательность
элементов
квадратных матриц называется побочной
диагональю.
Понятие главной диагонали и диагонального элемента распространяется и на прямоугольные матрицы.
Пример.
.
Диагональная матрица – квадратная матрица, у которой все элементы кроме элементов главной диагонали, равны нулю
.
Обозначается
.
Единичная матрица – диагональная матрица, у которой элементы главной диагонали равны единице. Обозначается буквой Е, или I
Нулевая матрица – прямоугольная матрица типа m×n, все элементы которой равны нулю. Обозначается буквой Θ или O
.
Верхняя треугольная матрица – квадратная матрица, у которой элементы, расположенные под главной диагональю равны нулю.
Нижняя треугольная матрица – квадратная матрица, у которой элементы, расположенные над главной диагональю, равны нулю.
Пример.
Трехдиагональные матрицы – квадратные матрицы, у которых ненулевыми элементами могут быть лишь диагональные и соседние с ними в строке (или в столбце).
Пример.
.
Верхняя трапециевидная матрица – прямоугольная матрица, у которой элементы, расположенные под главной диагональю, равны нулю.
Нижняя трапециевидная матрица – прямоугольная матрица, у которой элементы, расположенные над главной диагональю, равны нулю.
Пример.
,
.
Ступенчатая матрица (матрица ступенчатого вида) – прямоугольная матрица типа m×n, если для любой ее строки выполняется условие: под первым слева ненулевым элементом строки и под предшествующими ему нулевыми элементами строки все элементы матрицы равны нулю.
Примеры.
,
,
,
.
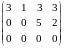С точки зрения программирования матрицы – это двумерные массивы чисел.