2. Первый закон термодинамики

2.1. Взяв V₁= 2 л одноатомного газа при р₁ = 10⁵ Па и Т₁ = 300 К, нагрели его до Т₂ = 320 К, уменьшив его объем до V₂=1 л. Процесс провели так, что на диаграмме (р, V) он изображается прямой линией. Определить работу газа и изменение его внутренней энергии.

2.2. Моль гелия нагревают от температуры T₁ до T₂. Процесс проводят так. что давление гелия пропорционально его объему. Определить работу гелия и его теплоемкость в этом процессе.

2.3. Найти молярную теплоёмкость С одноатомного газа в процессе, при котором Т=αр² (α – постоянная).

3. Циклические процессы

2.1. С молем идеального газа проводится циклический процесс, состоящий из двух изобар и двух изохор (рис. 2.1). Известны температуры T₁ и T₃, а также то, что точки 2 и 4 лежат на одной изотерме. Определить работу газа за цикл.

2.2. С некоторым газом (не обязательно идеальным) провели два процесса: 0-1 и 0-2, показанных на рис. 2.2, причем конечные состояния 1 и 2 лежат на одной адиабате. В каком процессе к газу подвели больше тепла? Ответ обосновать.

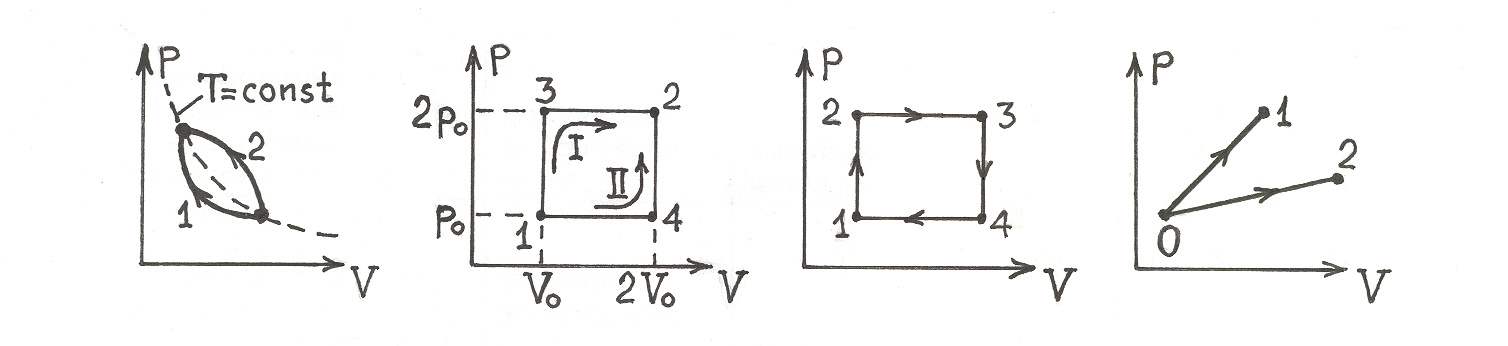
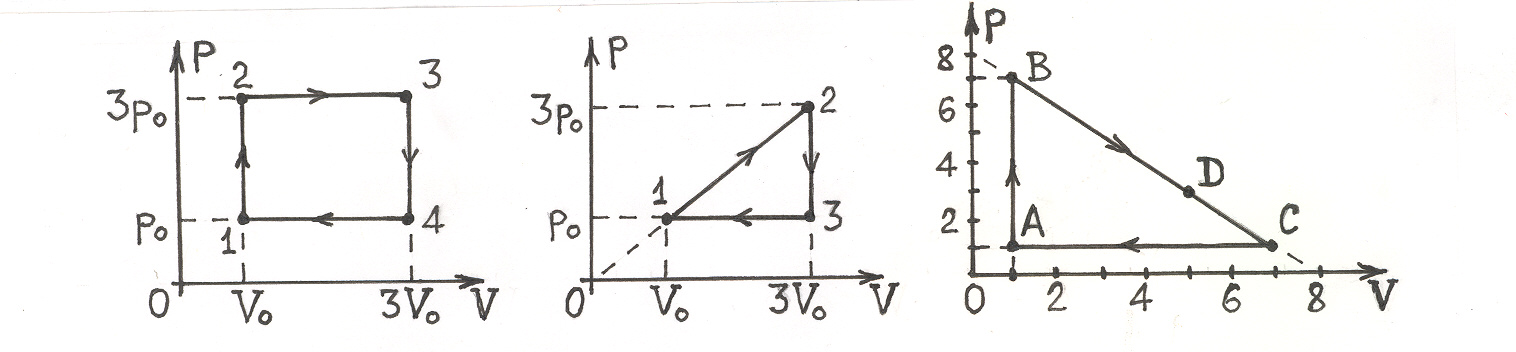
Рис. 2.1 Рис. 2.2 Рис. 2.3

2.3. Определить КПД цикла, показанного на рис. 2.3, если рабочим телом является одноатомный идеальный газ.

7. Задачи семинаров

1. Кинематика точки

1.1. (1.1). Первую половину суток паровоз шел со скоростью υ₁=60 км/ч, а вторую половину – со скоростью υ₂=90 км/ч. Вычислить среднюю скорость паровоза за сутки.

Ответ. <υ>=(υ₁+υ₂)/2=75 км/ч.

1.2. (1.2). Первую половину пути паровоз прошел со скоростью υ₁=60 км/ч, а вторую половину – со скоростью υ₂=90 км/ч. Вычислить среднюю скорость паровоза на всём пути.

Ответ. <υ>=2υ₁υ₂/(υ₁+υ₂)=72 км/ч.

1.3. (1.3). Ежедневно от А до Б и обратно летает вертолёт без посадки в Б. Скорость вертолёта относительно воздуха υ=108 км/ч. Вчера было тихо, а сегодня вдоль курса подул ветер со скоростью u=20 м/с. Во сколько раз изменится время полёта?

Ответ. Увеличилось в υ²/(υ²−u²)=1,8 раза.

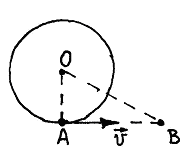
1.4. (1.21*). В некоторый момент времени скорость объекта А, находящегося на вращающейся карусели, с точки зрения неподвижного наблюдателя В равна . Каковы величина и направление скорости объекта В с точки зрения наблюдателя А, если ОА=R, OB=2R?

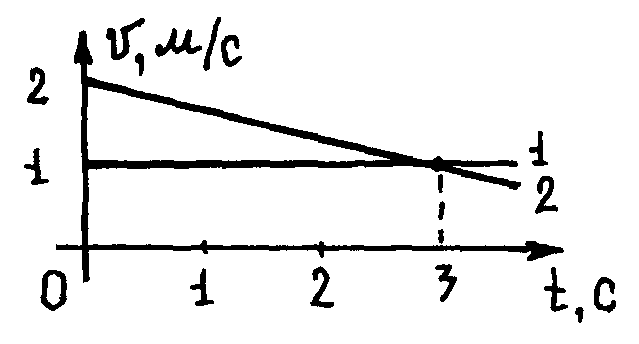Ответ. , .

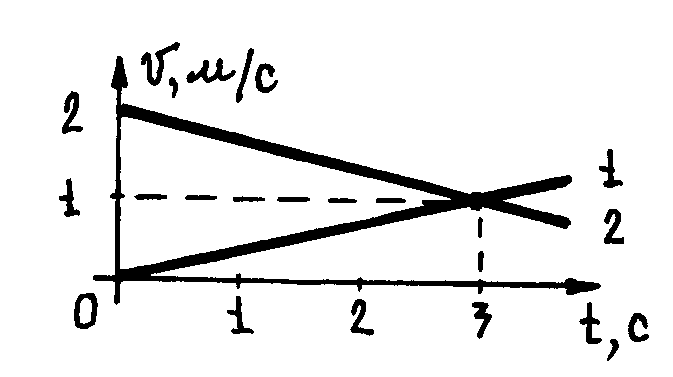
1.5. (1.28). Две частицы начинают движение вдоль оси х из точки х=0. Графики υ(t) частиц показаны на рисунке. Определить время и точку, где частицы встретятся вновь. Построить графики х(t).

Ответ. t=6 с, х=6 м.

1.6. (1.29). Две частицы начинают движение вдоль оси х из точки х=0. Графики υ(t) частиц показаны на рисунке. Определить время и точку, где частицы встретятся вновь. Построить графики х(t).

Ответ. t=6 с, x=6 м.

1.7. (1.30). Тело начинает двигаться из состояния покоя с постоянным ускорением. В первую секунду оно проходит путь 1 м. Сколько метров оно пройдет за вторую секунду?

Ответ. 3м.

1.8. (1.36). Поезд, двигаясь под уклон, прошел путь 340 м за 20 с и достиг скорости υ₂= 19 м/с. Найти скорость υ₁ поезда в начале уклона.

Ответ. 15 м/с.

1.9. (1.37). Тело движется равноускоренно с начальной скоростью υ₀=1 м/с. Пройдя некоторый путь, оно приобрело скорость υ₁=7 м/с. Вычислить скорость тела на середине этого пути. Ответ. 5 м/с.

1.10. (1.50). Камень бросили вертикально вверх со скоростью υ₀=20 м/с. Через какое время он будет находиться на высоте h=15 м и какую он при этом будет иметь скорость? Изобразить график движения камня у(t).

Ответ. t=1 с, 3 с; υ=10 м/с..

1.11. (1.51). Камень, брошенный вертикально вверх, находился на высоте 15 м два раза с интервалом 2 с. Определить начальную скорость камня.

Ответ. υ₀=20 м/с.

1.12. (1.61). Камень бросили с земли с начальной скоростью υ₀ под углом α к горизонту. Определить: 1) время полета ; 2) дальность полета s; 3) высоту полета h; 4) уравнение траектории у(х).

Ответ. 1) ; 2) ; 3) ;

4) , где , b=tg .

1.13. (1.64). Шарик бросают горизонтально. Во сколько раз увеличится дальность полета, если вдвое увеличить: а) начальную скорость; б) высоту, с которой бросают шарик ?

Ответ. а) в 2 раза; б) в раза.

1.14. (1.65). Двое играют в мяч, бросая, его друг другу. Какой наибольшей высоты достигает мяч, если от одного игрока до другого он летит 2 с?

Ответ. 5 м.

1.15. (1.66). При каком угле бросания дальность полета камня равна высоте его подъёма?

Ответ. tg  = 4,  = 76.

1.16. (1.71). Снаряд вылетает из пушки со скоростью υ₀=600 м/с. Под каким углом  надо выставить ствол, чтобы снаряд упал на расстоянии s=18 км от пушки? Каково время его полета?

Ответ. ₁=15, ₂=75. t₁=31 с, t₂=116 c.