Дії над матрицями

Сума матриць А та В є нова матриця, елементи якої дорівнюють сумі відповідних елементів матриць А та В.

Приклад. Обчислити суму матриць А і В:

Розв’язок.

Добуток матриці на число К≠0 є матриця, елементи якої є добуток елементів вихідної матриці на число К.

Добуток двох матриць - це матриця, елемент якої складається із суми добутків елементів рядка i першої матриці з елементами стовпця j другої матриці. Щоб добуток існував, матриці повинні бути узгоджені, тобто число стовпців першої матриці дорівнює числу рядків другої матриці. Розмірність узгоджених матриць така: перша матриця має розмірність ( ), друга - ( ).

Приклад. Знайти добуток матриць А і В:

Розв’язок.

Для добутку матриць не завжди виконується комутативний закон, тобто АВ≠ ВА. Якщо АВ= ВА, то матриці називаються переставними.

Одинична матриця переставна для всіх матриць її розмірності.

Транспонуванням матриці називається математична дія, коли рядки матриці А записуються стовпцями. Ця дія позначається як А^Т, а матриця А^Т називається транспонованою.

Приклад. Транспонувати матрицю .

1.3. Обернена матриця

Якщо добуток двох квадратних матриць дорівнює одиничній матриці, тобто АС=Е, то матриця С називається оберненою по відношенню до А та позначається С=А^—1. матриця А є оберненою до матриці С, тобто А=С^-1. Тоді АА^-1=А^-1А=Е. Обернена матриця є переставною.

Властивості оберненої матриці:

– де

,

.

Для знаходження оберненої матриці виконуються такі дії.

1. Обчислюється визначник матриці А. Якщо , то матриця називається не виродженою, і в цьому випадку існує обернена матриця.

Обчислюються алгебраїчні доповнення кожного елемента а_i,j матриці А і записуються у вигляді матриці С.

2. Транспонується матриця алгебраїчних доповнень С.

3. Обчислюється обернена матриця за формулою:

(1.6)

Виконується перевірка .

Приклад. Знайти обернену матрицю для .

Розв’язок .

1. Обчислюємо визначник матриці А, розкладуючи його по першому рядку.

.

, тому обернена матриця існує.

2. Обчислюємо алгебраїчні доповнення всіх елементів.

,

,

.

Запишемо матрицю алгебраїчних доповнень

.

3. Транспонуємо матрицю С.

.

4. Обернена матриця .

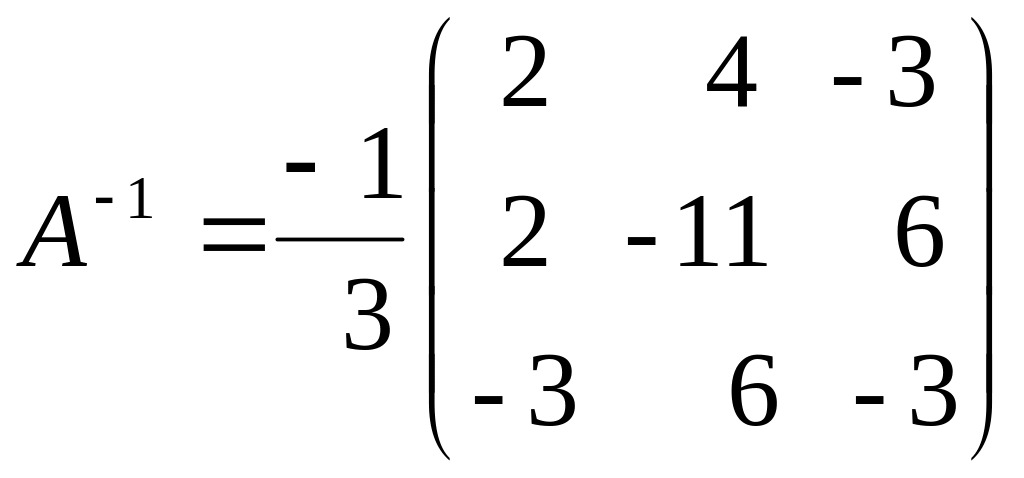Порада. Зручно обернену матрицю залишати у вигляді добутку числа на матрицю

Перевірка.

Приклад. Знайти обернену матрицю для матриці

Розв’язок.

1. Обчислюємо визначник матриці А, дописавши два стовпця

, тому обернена матриця існує.

2. Обчислюємо алгебраїчні доповнення всіх елементів.

,

,

.

3. С- матриця алгебраїчних доповнень.

.

4. Транспонуємо матрицю С.

.

5. Обернена матриця.

.

Перевірка

.

2. Загальна теорія систем лінійних рівнянь

Система лінійних рівнянь може мати один розв’язок, множину розв’язків, або не мати жодного розв’язку. Якщо визначник матриці коефіцієнтів системи лінійних рівнянь не дорівнює нулю, то система лінійних рівнянь має один розв’язок. Знаходження розв’язку системи лінійних рівнянь можна проводити за допомогою формул Крамера, методом оберненої матриці, або методом Гаусса.