Формула включень і виключень

Нехай дано дві скінченні множини А і В, перетин яких не порожній, тобто (або: дано дві події А і В, множини можливих значень яких містять спільні варіанти результату, тобто події сумісні). Треба знайти кількість елементів об’єднання цих множин .

Задача. Дано множини і . Визначити, скільки елементів містить їхнє об’єднання.

Розв’язання. Множини А і В містять відповідно по 3 і 4 елементи, тобто мають потужності , , а їхній перетин має потужність . В сумі потужностей множин двічі враховується кількість елементів перетину даних множин. Тому визначає кількість елементів об’єднання. З іншого боку, видно, що об’єднання цих множин має потужність .

Таким чином, маємо:

.

Якщо множин буде три, то, скориставшись властивостями операцій над множинами і одержаною формулою, матимемо:

.

► Приклад 10. На факультеті навчається 150 студентів. Усі вивчають іноземні мови. 120 з них вивчають англійську мову, а 80 ― німецьку. Скільки студентів вивчають одночасно дві мови?

Розв’язання. Спосіб I. Введемо позначення: — множина всіх студентів факультету (вона містить елементів); А — множина студентів, які вивчають англійську мову ( ); Н — множина студентів, які вивчають німецьку мову ( ); АН — множина студентів, які вивчають англійську й німецьку мови одночасно, і є перетином множин А і Н.

Зобразимо всю множину студентів відрізком і на ньому позначимо відрізками множини А і Н. Перетин множин А і Н дає множину АН.

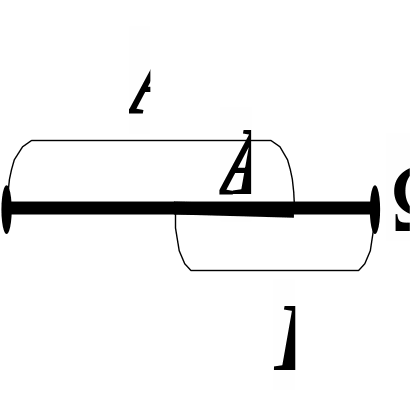
З одержаного малюнка видно, що для довжин відповідних відрізків виконується рівність

,

звідки одержуємо .

Дані множини можна зобразити також за допомогою діаграми Венна і скласти аналогічну рівність для площ

Метод математичної індукції

Коротко за допомогою предиката наведене формулювання методу математичної індукції можна подати так:

,

де запис означає, що формула Q є тотожно істинною (ще кажуть: тавтологією); твердження називається базою індукції, а формула — індукційним кроком.

Зауважимо, що в методі математичної індукції індукція може починатися не з , а з будь-якого числа ; при цьому твердження буде справедливим для всіх .

Приклад. Довести, що для будь-якого число ділиться на 6.

Розв’язання. Базою індукції є . Тому маємо . Одержане число ділиться на 6, тому база індукції виконується.

Щоб довести крок індукції, припустимо, що дане твердження є правильним для n, і доведемо, що воно буде правильним і для . Тому припустимо, що ділиться на 6. Тоді для матимемо:

.

В одержаному виразі перший доданок за припущенням індукції ділиться на 6. Покажемо, що другий доданок теж ділиться на 6. При цьому досить показати, що ділиться на 2. Але буде парним, якщо парне . Оскільки є добутком двох сусідніх натуральних чисел, серед яких одне парне, а інше — непарне, то одержане число є парним, а отже, число ділиться на 6.

Метод індукції дає можливість не тільки доводити твердження, а й виконувати побудову за індукцією і давати означення за індукцією.